Support Vector Machine(SVM) for Classification
1. Definition
서포트 벡터 머신(support vector machine, SVM)은 기계 학습의 분야 중 하나로 주어진 데이터 집합을 바탕으로 하여 새로운 데이터가 어느 카테고리에 속할지 판단하는 비확률적 이진 선형 모델이다(Reference).
$$\text {Training Data: } D = \{(x_1, y_1), \cdots , (x_n, y_n) \} \in x \times \{-1, 1\}, \, x \in R^d $$
$$ H = \{x \to sign(w^tx_i + b), \, w \in R^d, \, b \in R \} $$
$$h(x): \, x \to \{-1,1\} \text { in } H$$
SVM은 집합 $H$에서 클래스를 잘 분류하며 margin(여백)이 가장 큰 hyper-plane $h(x) = w^tx + b$를 찾는 것을 목적으로 한다. Hyper-plane이란, 데이터 집합을 분리하는 선(2차원) 또는 면(3차원) 등을 일반화한 개념이다. Margin이란, hyper-plane과 그것과 가장 가까이 있는 훈련 데이터(support vector)와의 거리를 의미한다(Reference).
[Example]
서로 다른 범주의 데이터를 잘 분류하는 hyper-plane $A$와 $B$가 존재한다($H = \{A, B\}$).
$$A = h_1(x) = w_1^tx + b_1$$
$$B = h_2(x) = w_2^tx + b_2 $$
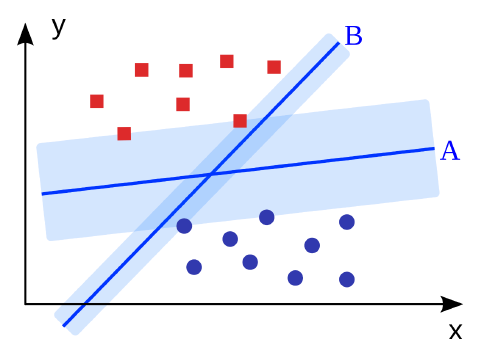
SVM에서는 hyper-plane $A$와 $B$ 중 margin이 더 큰 $A$를 더 선호한다. 이에 대한 이유 및 자세한 알고리즘을 설명해 보고자 한다.
<<< (Hard) SVM에서의 key point >>>
margin의 바깥에서 클래스가 분류되도록 하면서 margin을 최대화하는 hyper-plane을 찾는 것
2. Formulation
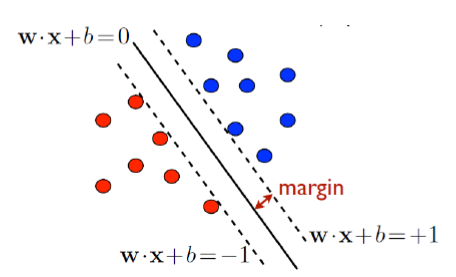
주어진 데이터 $D$를 통해 각 클래스(red or blue)를 잘 분류하면서 margin이 가장 큰 normal vector $w$(가정: $||w||=1$)와 bias $b$를 구하는 것이 SVM의 목적이다.
- 데이터 집합을 분리하는 hyper-plane: $w^tx - b = 0$($w$: 초평면의 법선 벡터)
- $X^+$(support vector): $y_i = +1$의 데이터 중에서 hyper-plane과 가장 가까운 데이터
- $X^-$(support vector): $y_i = -1$의 데이터 중에서 hyper-plane과 가장 가까운 데이터
- 주어진 hyper-plane과 같은 normal vector를 가지면서 $X^+$를 지나는 hyper-plane: $w^tx + b = +1$
- 주어진 hyper-plane과 같은 normal vector를 가지면서 $X^-$를 지나는 hyper-plane: $w^tx + b = -1$
- Margin = $\dfrac{1}{||w||^2}$
$w^t x + b = 0$ 위에 존재하는 점을 $x_0$, $w^tx + b = 1$ 위에 존재하는 점을 $x_1$ 그리고 $x_0$를 $x_1$의 $w^tx + b = 0$ 위로의 정사영한 점이라고 가정해본다.
- $w^tx_0 + b = 0$ & $w^tx_1 + b =1$
- $x_1 = \rho w+ x_0$ ($\rho : \text {distance between } x_0 \text{ and } x_1$)
- $w^t(\rho w+ x_0)+b=1, \, w^t\rho {w}+w^tx_0 + b = 1, \, \rho = \dfrac {1}{w^tw}=\dfrac {1}{||w||_2}(\because w^tx_0 + b = 0)$
위의 과정을 통해 margin의 크기는 $\dfrac {1}{||w||_2}$임을 알 수 있다. Margin을 구하는 자세한 과정은 이 블로그를 참조하면 좋을 거 같다.
그렇다면 왜 margin의 크기를 최대화해야 하는가?
먼저, shatter 및 vc dimension, SRM에 대한 개념을 알아야 한다.
Shatter란?
특정 함수 $F$에 의해 $n$개의 점을 오류 없이 임의의 +1 또는 -1을 target 값으로 하는 binary classification이 가능한 경우를 의미한다. 즉, 어떤 점들이 주어졌을 때 특정한 형태의 함수가 해당하는 점들이 가질 수 있는 binary classification 결과물에 모든 조합을 생성해 낼 수 있으면 shatter하다고 하고 생성해 낼 수 없으면 shatter하지 않는다고 말한다.
특정 함수 형태의 집합 $F$에 의해 $n$개의 점을 오류 없이 임의의 +1 또는 -1을 target 값으로 하는 binary classification이 가능한 경우를 의미한다. 즉, 어떤 점들이 주어졌을 때 특정한 형태의 함수가 해당하는 점들이 가질 수 있는 모든 binary 조합을 분류하는 함수가 $F$의 원소로 존재하면 shatter하다고 하고 생성해 낼 수 없으면 shatter하지 않는다고 말한다.
※ 직선분류기의 경우, $n$차원에서 데이터(점)을 최대 $(n+1)$개까지 shatter 할 수 있다.
VC dimension이란?
분류기의 복잡도를 측정하는 지표이며 함수 $F$에 의해 shatter되는 점들의 최대 개수를 의미한다.
Structure Risk Minimization(SRM)이란?
학습 데이터 수($n$)와 vc dimension을 알고 있는 경우, training error와 capacity term의 합을 함께 control하는 적절한 model 찾는 것이다.
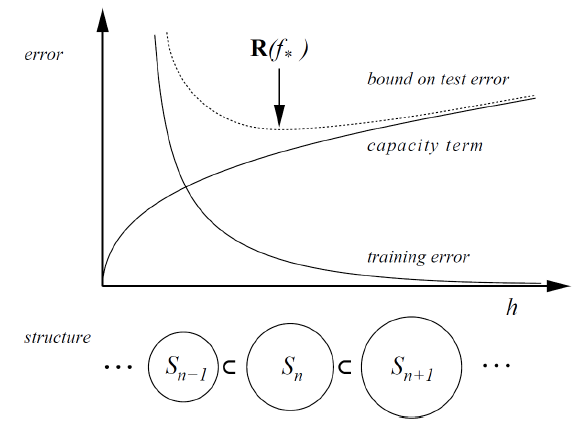
[Figure 3]에서 $x$축은 complexity of model를 의미한다. 모델의 복잡성($h$)이 증가할수록 training error는 감소하는 반면 capacity term은 증가하는 것을 알 수 있다. Capacity term이 증가한다는 것은 모델이 복잡해질수록 noise까지 외워버리는 능력이 생성된다는 것을 의미하며 오히려 일반화 성능을 악화시킨다. SRM은 training error와 capacity term을 모두 고려한 것이며 SRM 값이 가장 작은 model을 최적의 model로 판단한다.
- training error = $R_{emp}[f]=\dfrac{1}{n}\sum^n_{i=1}L(f(x_i),y_i)$
- Structural Loss = training error + capacity term = $R_{emp}[f]+\sqrt{\dfrac{h(ln\dfrac{2n}{h}+1)-ln\dfrac{\delta}{4}}{n}}, \, \delta \geq 0$
- n = 학습 데이터 수
- $0 < \delta < 1$
- h = vc dimension
이제 margin과 VC dimension간의 관계성에 대해 살펴보고자 한다.
$$h \leq min([\dfrac{R^2}{\vartriangle^2}],D)+1$$
$$h \leq min\left(\left[\dfrac{R^2}{\vartriangle^2}\right],D\right)+1$$
- h : VC dimension
- R : 전체 Data를 감싸는 초구의 반지름(고정된 값)
- $\vartriangle$: 마진(변하는 값)
- D : 차원수(고정된 값)
만약, margin이 큰 경우, $h \leq min([\dfrac{R^2}{\vartriangle^2}],D)+1$이고, margin이 작은 경우, $h \leq D+1$이다. 어떤 함수의 리스크를 줄이는데 training error가 같다면 결국 margin이 최대가 되는 점을 찾으면 $h \text{(=vc dimension)}$ 값이 작아지기 때문에 capacity term이 감소한다. 따라서, 기대할 수 있는 리스크(structurl loss)가 감소하기 때문에 최적의 모형을 찾을 수 있다.
따라서, SVM의 목적은 $\text{argmax}_x{\dfrac{2}{||w||_2}} = \text{argmin}_x{\dfrac{||w||^2_2}{2}}$을 구하는 것이다.
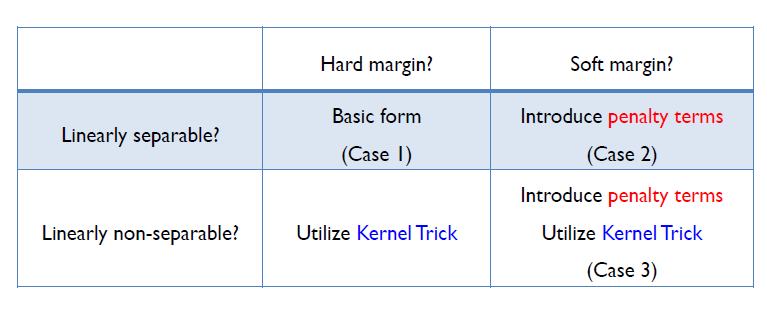
SVM은 크게 hard margin svm과 soft margin svm으로 분류할 수 있다.
- (Case 1): Hard Margin Linear SVM
- (Case 2): Soft Margin Linear SVM
- (Case 3): Soft Margin Non-Linear SVM
Hard의 의미는 hyper-plane을 기준으로 오분류를 허용하지 않고 완벽하게 분류하는 방법이며 클래스들이 선형 함수로 완벽하게 분리되는 Linear Separable한 경우에만 사용 가능하다. 하지만, 현실세계에서 완벽하게 Linear Separable한 경우는 거의 없다.
Soft는 margin을 최대화되 penalty term을 도입해 오분류를 어느 정도 허용하는 방법이다(Reference).
Hard margin svm의 경우, 오분류를 허용하지 않기 때문에 soft margin svm보다 상대적으로 margin이 작을 것이다. 개별적인 학습 데이터를 다 놓치지 않기 위해 오분류를 허용하지 않는 hyper-plane을 찾을 경우, overfitting 문제 발생 가능성이 존재한다.
반대로, soft margin svm의 경우, 오분류가 허용되기 때문에 margin을 너무 크게 잡을 경우 underfitting 문제 발생 가능성이 존재한다.
※ Overfitting(과대적합)은 기계 학습에서 학습 데이터를 과하게 학습하는 것.
※ Underfitting(과소적합)은 기계 학습에서 통계 모형의 능력 부족으로 학습 데이터를 충분히 설명하지 못하도록 부족하게 학습된 것.
먼저, 우리는 "Case 1"에 대해서 다루어 보고자 한다.
3. Hard Margin SVM
[Objective function]
Hard margin SVM의 objective function은 다음과 같다.
$$ \begin{gathered} &
\min f(w) = \min \dfrac{\|w\|^2}{2} \\ &
\text{ s.t. }y_i\left(w^tx_i-b \geq 1\right) \forall{i}
\end{gathered} $$
- $\text{Objective Function: } \min f(w) = \min \dfrac{\|w\|^2}{2}$
- $\text { Constraint : } g = y_i\left(w^tx_i + b \geq 1\right) \forall{i}$
- $y_i = +1$인 $x_i$에 대해서 $w^t \cdot x_i + b \geq +1$
- $y_i = -1$인 $x_i$에 대해서 $w^t \cdot x_i + b \leq -1$
Parameter $w$와 $b$는 Quadratic Programming(QP)를 통해 찾을 수 있다.
자세한 내용은 [Section 4. Soft Margin Linear SVM]에서 살펴본다.
[Decision Function]
새로운 데이터가 들어왔을 때 binary classification하는 기준은 다음과 같다.
$$ h(x_{new}) = sign({w^*}^t x_{new}+ b^*) \in \{-1,1\}$$
4. Soft Margin Linear SVM
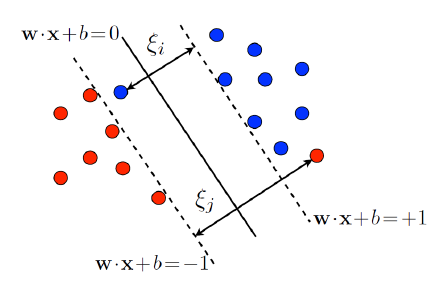
[$\xi_i$에 대한 설명]
Soft margin SVM의 경우, 오분류된 데이터도 허용한다.
[Figure 5]에서 오분류된 데이터인 빨간색 점의 위치 및 라벨을 $\mathbf{x}' = (x_1', x_2')$, $y'=-1$로 명시하겠다.
빨간색 점의 실제 라벨은 $-1$인 반면, $w^t \mathbf{x} + b \geq 1$ 영역에 존재한다. 빨간색 점과 $w \mathbf{x} + b = -1$ 사이의 거리를 계산하면 다음과 같다.
$$\dfrac{|w^t \mathbf{x}' + b + 1|}{||w||} = \dfrac{(w^t \mathbf{x}' + b)+1}{||w||} = \dfrac{-y'(w^t \mathbf{x}' + b) + 1}{||w||} \tag{1}$$
식 $(1)$을 응용하여 $\xi_i$를 다음과 같이 정의하겠다.
$$\xi_i = \max(0, 1 - y'(w^t\mathbf{x}' + b))$$
"첫번째 case: $\xi_i=0$"
$\xi_i = 0$이라는 것은 $i$번째 객체는 정분류된 데이터임을 의미한다. → $1 - y_i(w^t \mathbf{x}_i + b) < 0$ → $y_i(w^t \mathbf{x}_i + b) > 1 \geq 1 - \xi_i$
"두번째 케이스 $\xi_i > 0$"
$\xi_i > 0$이라는 것은 $i$번째 객체는 오분류된 데이터임을 의미한다. → $1 - y_i(w^t \mathbf{x}_i + b) = \xi_i $ → $y_i(w^t \mathbf{x}_i + b) = 1 - \xi_i$
[Objective function]
Soft margin linear svm의 objective function은 다음과 같다.
$$ \begin{gathered} &
\min f(w) = \min \dfrac{\|w\|^2}{2} \ + C\sum^n_{i=1}\xi_i \\ &
\text{ s.t. }y_i(w^tx_i-b) \geq 1 - \xi_i , \, \xi_i \geq 0 \, \forall{i}
\end{gathered} $$
- $\text{Objective Function: } \min f(w) = \min \dfrac{||w||^2}{2} + C\sum^n_{i=1}\xi_i$
첫번째 term인 $\dfrac{||w||^2}{2}$은 margin을 최대화하는 term이다.
두번째 term인 $C \sum^n_{i=1} \xi_i$은 penalty term이며 $C$는 하이퍼-파라미터이다.
- $\text { Constraint : } g = y_i(w^t \cdot x_i-b) \geq 1 - \xi_i , \, \xi_i \geq 0 \, \forall{i}$
▶ Penalty term이 존재하는 이유
Soft margin SVM의 경우 오분류된 데이터도 허용합니다. 하지만 오분류된 데이터를 너무 많이 허용하면 안되기 때문에 $\xi_i$를 이용하여 penalty term을 추가해 줍니다.
오분류된 데이터 혹은 마진 안에 존재하는 데이터에 대해서는 penalty를 부여하고($\to \, \xi_i > 0$),
정분류된 데이터에 대해서는 penalty를 부여하지 않는다($\to \, \xi_i=0$).
※ 점선과 실선 사이에 존재하는 객체(→ 여백 안에 존재하는 객체)도 $\xi_i > 0$입니다.
[Figure 5]에서 점선과 실선 사이에 존재하는 객체인 파란색 점에 대해서 패널티를 부여하지 않을 경우, 여백이 좁아져 과적합(over-fitting) 문제가 발생할 수 있습니다. 이러한 관점에서 여백 안에 존재하는 객체도 오분류된 데이터로 판단합니다.
Optimal solution $w^*$와 $b^*$은 Quadratic Programming을 통해 찾는다.
먼저, 제약조건이 존재하기 때문에 lagrangin problem을 이용해 하나의 식으로 표현해준다.
[Lagrangian Problem(Primal Problem)]
- Given Data = ${(x_i, y_i)}^n_{i=1}$
- parameter = ${(w,b,\xi_i)}^n_{i=1}$
- hyper-parameter = C (찾는 방법: Manual Search, Grid Search, Random Search, Bayesian Optimization)
$$\min L_p(w,b,\xi_i,\alpha_i,\mu_i) = \dfrac{1}{2}||w||^2+C\sum^n_{i=1}\xi_i-\sum^n_{i=1}\alpha_i(y_i(w^t \cdot x_i -b)-1+\xi_i)-\sum^n_{i=1} \mu_i \xi_i \\ s.t. \alpha_i \geq 0, \mu_i \geq 0$$
- $\alpha_i$ , $\mu_i$ : Lagrangian Multiplier
[KKT condition]
(Stationary)
$$\dfrac{\partial{L_p}}{\partial{w}}=w-\sum^n_{i=1}\alpha_iy_ix_i=0, \, \to \, w^* = \sum^n_{i=1}\alpha_iy_ix_i \tag{K1}$$
$$\dfrac{\partial{L_p}}{\partial{b}}=\sum^n_{i=1}\alpha_iy_i=0 \tag{K2}$$
$$\dfrac{\partial{L_p}}{\partial{\xi_i}}=C-\alpha_i-\mu_i, \forall i \tag{K3}$$
(Complementary Slackness)
$$\alpha_i[y_i(w^tx_i + b) - 1 +\xi_i] = 0, {}^{\forall} i \tag{K4}$$
$$\eta_i \xi_i = 0 \implies (C-\alpha_i)\xi_i=0, {}^{\forall} i \tag{K5}$$
[Dual Problem]
$(K1)$, $(K2)$, $(K3)$을 이용해 Dual Problem으로 식 $(2)$와 같이 표현할 수 있다.
$$\max L_D(\alpha_i) = \sum^n_{i=1}\alpha_i-\dfrac{1}{2}\sum^n_{i=1}\sum^n_{j=1}\alpha_i\alpha_jy_iy_jx_i^tx_j \\ s.t. \sum^n_{i=1}\alpha_iy_i=0, 0 \leq \alpha_i \leq C \tag{2}$$
식 $(2)$에 대해서 음수를 취해줌으로써 식 $(3)$과 같이 최소화하는 문제로 변한시켰다.
$$ \begin{align} \text{Find } \alpha \;\;\text{ s.t Minimize }\;\; \frac{1}{2}\alpha^tQ\alpha-e^t\alpha \\ \text{Subject to } y^t\alpha=0 \\ \;\; 0\leq \alpha_i \leq C, \;\forall i \end{align} \tag{3}$$
- $y = (y_1, \cdots, y_n)^T$
- $e = (1, 1, \cdots, 1)^T$
- $Q \in \mathbb{R}^{n \times n}$
- $Q_{ij} = y_iy_jx_i^Tx_j$
"" $w$와 $b$의 최적해 """
식 $(3)$을 통해 찾은 $\alpha^*$과 KKT 조건을 이용하여 $w^*$와 $b^*$를 찾을 수 있다.
$w$는 식 $(K1)$에 의해 쉽게 구할 수 있다.
$$ w^* = \sum^n_{i=1} \alpha^*_i y_i x_i $$
$b$와 같은 경우는 다음과 같이 구할 수 있다.
식 $(4)$를 만족하는 index set $I$를 찾습니다.
$$ I = \{i \in \{1,2,\cdots, n\} : 0 < \alpha_i < C\} \tag{4}$$
$(K5): (C-\alpha_i) \xi_i = 0$에 의해, $C-\alpha_i \ne 0$이므로 $\xi_i = 0$이다.
$(K4): \alpha_i[y_i(w^tx_i + b) -1 + \xi_i] = 0$에 의해 $\alpha_i \ne 0, \xi_i =0$이므로 $y_i(w^t x_i + b)=1$이 성립된다.
$y_i(w^t x_i + b) = 1 \\ w^tx_i + b = \dfrac{1}{y_i} = y_i (\because y_i = \dfrac{1}{y_i} \in \{-1,1\}) \\ b = y_i - w^tx_i = y_i - \sum^n_{j=1} \alpha_j y_j x^T_j x_i$
따라서, 최종적으로 $b^*$은 다음과 같이 유도할 수 있다.
$$\begin{align} b^* &= \dfrac{1}{|I|} \sum_{i \in I}(y_i - w^* \cdot x_i) \\ &= \dfrac{1}{|I|} \sum_{i \in I}(y_i - \sum^n_{j=1} \alpha_j y_j x^T_j x_i) \end{align}$$
[Decision Function]
결정경계선인 decision function은 다음과 같다.
$$ h(x_{new}) = sign({w^*}^t \cdot x_{new} + b^*) \in \{-1,1\}$$
마지막으로 soft margin linear svm에서의 support vector 의미 및 support vector만이 optimal solution을 구하는데 영향력을 끼침을 보여주고 hyper-parameter $C$에 대해 간단하게 설명하고 마치고자 한다.
[Support Vector]
$(K4), (K5)$에 의해 아래 두 식이 성립한다.
- $\alpha_i(y_i(w^t \cdot x_i + b) -1 + \xi_i ) = 0$
- $\mu_i \xi_i = 0$
우리는 $C_i - \alpha_i - \mu_i =0 $와 $ 0 < \alpha_i < C$에 대해서도 고려하여 다음 3가지 case에 대해 다루어 볼 것이다.
"Case 1" : $\alpha_i=0$인 경우,
- $y_i(w^t \cdot x_i + b) -1 + \xi_i \ne 0$
- $\mu_i = C_i \, \to \, \xi_i = 0$
두 식에 의해 $i$번째 객체는 margin 바깥에 존재하며($y_i(w^t \cdot x_i + b) -1 + \xi_i \ne 0$) 잘 분류된 객체($\xi_i = 0$)임을 알 수 있다. "Case 1"에 해당하는 $i$번째 객체는 non-support vector이다.
"Case 2" : $0 < \alpha_i < C$인 경우,
- $y_i(w^t \cdot x_i + b) -1 + \xi_i = 0$
- $\mu_i = C_i - \alpha_i > 0 \, \to \, \xi_i = 0 \, \to \, y_i(w^tx_i + b) = 1$
두 식에 의해 $i$번째 객체는 $w^t \cdot x_i + b - 1 = 0$ 혹은 $w^t \cdot x_i + b + 1 = 0$ 위에 존재하는 객체이며 잘 분류된 객체($\xi_i = 0$)임을 알 수 있다. "Case 2"에 해당하는 $i$번째 객체는 support vector이다.
"Case 3" : $\alpha_i = C \ne 0$인 경우,
- $y_i(w^t \cdot x_i + b) -1 + \xi_i = 0$
- $\mu_i = 0 \, \to \, \xi_i \ne 0 $
두 식에 의해 $i$번째 객체는 $w^t \cdot x_i + b - 1 < 0$ 혹은 $w^t \cdot x_i + b + 1 > 0$ 영역에 존재하는 객체이며 오분류된 객체($\xi_i > 0$)임을 알 수 있다. "Case 3"에 해당하는 $i$번째 객체는 support vector이다.
즉, support vector는 $\alpha_i \ne 0$인 객체를 의미한다. 이는 optimal solution $w^*$와 $b^*$를 찾는데 영향을 끼치는 객체는 support vector임을 알 수 있다.
[Hyper-parmaeter $C$]
Soft margin svm의 objective function을 확인해보면, 하이퍼 파리미터 $C$ 값이 존재한다. $C$ 값에 따라 margin의 크기가 다르다.
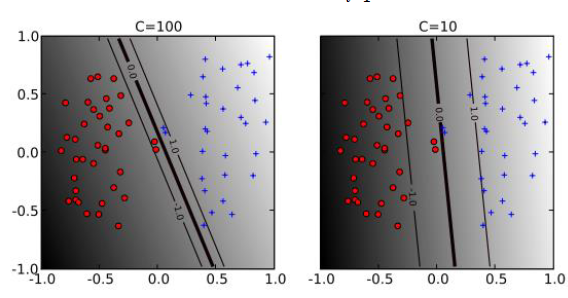
- $C$가 큰 경우, 왠만하면 오분류된 데이터를 허용하지 않겠다는 것을 의미한다. 즉, margin의 크기가 좁다.
- $C$가 작은 경우, 오분류된 데이터를 어느 정도 허용하겠다는 것을 의미한다.즉, margin의 크기가 넓다.
지금까지는 서로 다른 범주의 데이터를 선형으로 분리가능한 경우에 다루었다. 만약, 데이터를 선형으로 분리할 수 없는 경우는 어떻게 해야할까? 이에 대한 방안으로 도입된게 "kernel svm"이다.
5. Soft Margin Non-Linear SVM(Kernel SVM)

[Figure 7]에서와 같이 서로 다른 범주의 데이터를 linearly separable 할 수 없는 경우 linear model로 데이터를 binary classification 할 수 없다. 이에 대한 해결책으로 input vector $x \in R^d$를 linear model이 해결할 수 있는 형태인 feature space $\phi(x)$로 만드는 방법이 있다. 하지만, feature map을 찾는 것 자체가 매우 어려우며 svm의 경우 내적 $\phi(x_i) \cdot \phi(x_j)$ 연산량도 엄청나다는 문제점이 존재한다. 이 두 문제점을 동시에 해결하기 위해 고안된 방법이 Kernel Function이다.
[Figure 7]에서와 같이 서로 다른 범주의 데이터를 linearly separable 할 수 없는 경우 linear model로 데이터를 binary classification 할 수 없다. 이에 대한 해결책으로 input vector $x \in R^d$를 linear model이 해결할 수 있는 형태인 feature space $\phi(x)$로 mapping한 뒤에 SVM을 진행하는 방법이 있다. 하지만, 적절한 $\phi(x)$을 찾는 것 자체가 매우 어려우며 svm의 경우 mapping 시키는 연산과 내적 $\phi(x_i) \cdot \phi(x_j)$ 연산량도 엄청나다는 문제점이 존재한다. 이 두 문제점을 동시에 해결하기 위해 고안된 방법이 Kernel Function이다.
※ Feature map이랑 kernel function에 대한 설명은 이 블로그를 참조하면 좋을 거 같다.
[Kernel Trick]: kernel function을 이용한 linear technique
$$K(x_i, xj) = \phi(x_i)^t \cdot \phi(x_j) = < \phi(x_i), \phi(x_j) >$$
Kernel function의 종류:
$$
\begin{array}{rll}
\text { linear } & : \quad K\left(x_1, x_2\right)=x_1^T x_2 \\
\text { polynomial } & : \quad K\left(x_1, x_2\right)=\left(x_1^T x_2+c\right)^d, \quad c>0 \\
\text { sigmoid } & : \quad K\left(x_1, x_2\right)=\tanh \left\{a\left(x_1^T x_2\right)+b\right\}, \quad a, b \geq 0 \\
\text { gaussian } & : \quad K\left(x_1, x_2\right)=\exp \left\{-\frac{\left\|x_1-x_2\right\|_2^2}{2 \sigma^2}\right\}, \quad \sigma \neq 0
\end{array}
$$
이미 $\phi(x)$의 내적 계산이 가능한 kernel들이 공개되어 있기에 우리는 $\phi(\cdot)$가 어떤 함수인지는 몰라도 된다. 즉, cost funciton이 감소한다.
이미 $\phi(x)$의 내적 계산이 가능한 kernel들이 공개되어 있기에 우리는 $\phi(\cdot)$가 어떤 함수인지는 몰라도 된다. 즉, mapping을 위한 계산 cost가 감소한다.
이제 본격적으로 soft margin non-linear svm의 알고리즘에 살펴보고자 한다. 기존의 linear svm과 형태상 비슷하지만, input vector $x$를 $\phi(\cdot)$을 통해 feature space상으로 mapping 했다는 점과 kernel trick을 이용한다는 점에서 차이가 존재한다.
[Objective function]
$$ \begin{gathered}
\min \frac{1}{2}\|w\|^2+C \sum_{i=1}^n \xi_i \\
y_i\left(w^t \cdot \phi\left(x_i\right)+b\right) \geq 1-\xi_i, \xi_i \geq 0, \forall{i}
\end{gathered} $$
$$ \begin{gathered}
\min \frac{1}{2}\|w\|^2+C \sum_{i=1}^n \xi_i \\
\text{with} \ \ y_i\left(w^t \cdot \phi\left(x_i\right)+b\right) \geq 1-\xi_i, \xi_i \geq 0, \forall{i}
\end{gathered} $$
- $\phi(\cdot) : $ feature mapping function($R^d \to R^p \, (d < p)$)
[Lagrangian Problem(Primal Problem)]
$$\min L_p(w,b,\xi_i,\alpha_i,\mu_i) = \dfrac{1}{2}||w||^2+C\sum^n_{i=1}\xi_i-\sum^n_{i=1}\alpha_i(y_i(w^t \cdot \phi(x_i)+b)-1+\xi_i)-\sum^n_{i=1}\mu_i\xi_i$$
[KKT condition]
(Stationary)
$$\dfrac{\partial{L_p}}{\partial{w}}=w-\sum^n_{i=1}\alpha_iy_i\phi(x_i)=0, \, \to \, w^* = \sum^n_{i=1}\alpha_iy_i\phi(x_i)$$
$$\dfrac{\partial{L_p}}{\partial{b}}=\sum^n_{i=1}\alpha_iy_i=0$$
$$\dfrac{\partial{L_p}}{\partial{\xi_i}}=C-\alpha_i-\mu_i, \forall i$$
(Complementary Slackness)
$$\alpha_i[y_i(w^t \phi(x_i) + b) - 1 + \xi_i] = 0, {}^{\forall} i $$
$$\eta_i \xi_i = 0 \implies (C-\alpha_i)\xi_i=0, {}^{\forall} $$
[Dual Problem]
$$\max L_D(\alpha_i) = \sum^n_{i=1}\alpha_i - \dfrac{1}{2}\sum^n_{i=1}\sum^n_{j=1}\alpha_i\alpha_j\phi(x_i)^t\phi(x_j), \\ s.t. \, \sum^n_{i=1}\alpha_iy_i=0, \, 0 \leq \alpha_i \leq C $$
※ Using Kernel trick
$$\max L_D(\alpha_i) = \sum^n_{i=1}\alpha_i - \dfrac{1}{2}\sum^n_{i=1}\sum^n_{j=1}\alpha_i\alpha_j k(x_i, x_j), \\ s.t. \, \sum^n_{i=1}\alpha_iy_i=0, \, 0 \leq \alpha_i \leq C \tag{5}$$
마찬가지로 식 $(5)$에 음수를 취함으로써 최소화 문제로 전환시켰다.
식 $(6)$을 최소로 하는 $\alpha^*$과 KKT 조건을 이용하여 $w^*$과 $b^*$를 찾을 수 있다.
$$\begin{align} \text{Find } \alpha \;\;\text{ s.t Minimize }\;\; \frac{1}{2}\alpha^tQ\alpha-e^t\alpha \\ \text{Subject to } y^t\alpha=0 \\ \;\; 0\leq \alpha_i \leq C, \;\forall i \end{align} \tag{6}$$
- $y=(y_1, y_2, \cdots, y_n)^T$
- $e=(1,1,\cdots, 1)^T$
- $Q \in \mathbb{R}^{n \times n}$
- $Q_{ij} = y_iy_j \phi(x_i)^T \phi(x_j)$
[Decision Function]
새로운 데이터가 들어왔을 때 binary classification하는 기준은 다음과 같다.
$$ h(x_{new}) = sign({w^*}^t \cdot \phi(x_{new}) + b^*) \in \{-1, 1\}$$
Kernel function 중 gaussian kernel function을 이용한 경우, soft margin non-linear svm의 hyper-parameter는 $C$와 $\gamma$이다.
- $C$: margin을 최대화하는 term과 penalty term 간의 trade-off 관계를 조절하는 parameter
- $\gamma$: hyper-plane을 얼마나 유연하게 그을지에 대해 정해주는 parameter
- $\gamma$ 값이 클수록($\sigma$ 값이 작을수록), 학습 데이터에 많이 의존하기 때문에 hyper-plane은 복잡해진다.
- $\gamma$ 값이 작을수록($\sigma$ 값이 클수록), 학습 데이터 의존도가 떨어지기 때문에 hyper-plane은 선형에 가깝다.
[Example]
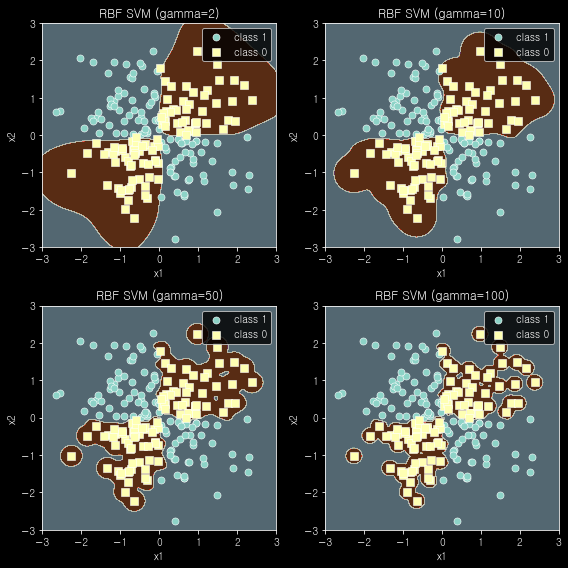
- 같은 cost 값에서, $\gamma$값이 작을수록 선형에 가까운 분류 경계면 생성되는 것을 확인할 수 있다.
- $\gamma$ 값이 커질수록, 즉 $\sigma$ 값이 작아질수록 hyper-parameter $C$ 값의 영향이 미미한 것을 알 수 있다.
- $\gamma$값이 커질수록, 즉 $\sigma$ 값이 작아질수록, hyper-plane에 가까이 있는 데이터 샘플에 대해서만 영향을 크게 받기 때문에 점점 더 구불구불해지는 것을 알 수 있다.
- 같은$\gamma$ 값에서, cost(C) 값이 큰 경우(penalty를 크게 준 경우), 좁은 margin이 생성된 것을 확인할 수 있음.
- Hyperparameter인 C값은 커질수록 이상치의 존재 가능성을 더 낮게 본다. 즉, 더 복잡한 hyper-plane이 형성된다.
※ $C$와 $\gamma$ 값 모두 너무 낮을 경우 under-fitting 위험이 존재하고 너무 큰 경우 over-fitting의 위험이 존재한다.
[Simulation]
모의 데이터를 통해 $\gamma$ 값이 [2, 10, 50, 100]인 경우에 대해 train dataset과 test dataset의 성능을 측정해 보았다.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
import pandas as pd
from sklearn.preprocessing import FunctionTransformer
from sklearn.pipeline import Pipeline
from sklearn.svm import SVC
# 데이터셋 생성
## train set
np.random.seed(0)
X_xor = np.random.randn(200,2) ## 정규분포로부터 (200,2) 추출 ## X_1, X_2 생성
Y_xor = np.logical_xor(X_xor[:,0]>0, X_xor[:,1]>0) ## 1개만 참인 경우 True, 두 개 모두 거짓인 경우에만 False
Y_xor = np.where(Y_xor, 1, 0)
## test set
np.random.seed(10)
X_test = np.random.randn(50,2) ## 정규분포로부터 (200,2) 추출 ## X_1, X_2 생성
Y_test = np.logical_xor(X_test[:,0]>0, X_test[:,1]>0) ## 1개만 참인 경우 True, 두 개 모두 거짓인 경우에만 False
Y_test = np.where(Y_test, 1, 0)
def svc_score(gamma,x_train, y_train, x_test, y_test):
model = SVC(kernel='rbf',gamma=gamma).fit(x_train,y_train)
train_score = model.score(x_train, y_train)
test_score = model.score(x_test, y_test)
return train_score, test_score
gamma = [2,10,50,100]
for i in gamma:
v = svc_score(i,x_train=X_xor, y_train=Y_xor, x_test=X_test, y_test=Y_test)
print('gamma가',i,'인 경우 (train_score), (test_score)는',v)| $\gamma$ | train score | test score |
| 2 | 0.985 | 0.94 |
| 10 | 0.995 | 0.9 |
| 50 | 1.0 | 0.86 |
| 100 | 1.0 | 0.84 |
[Figure 9]와 train set & test set 성능 결과를 확인해 보면, $\gamma$ 값이 너무 큰 경우, 복잡한 경계면을 생성하며 train set은 잘 예측하는 반면 test set 예측력이 떨어지는 것을 확인할 수 있다. 즉, over-fitting이 발생했다. $\gamma$ 값이 점점 커질수록, 결정 경계가 결정 경계 가까이에 있는 데이터 샘플에 크게 영향을 받기 때문에 점점 더 구불해지는 것도 [Figure 9]를 통해 확인할 수 있다.
본 글에서는 SVM의 3가지 case에 대한 algorithm 설명 및 모의실험을 통한 hyper-parameter 값에 따른 성능 차이를 확인해 보았다. 다음 글에서는 Support Vector Regression(SVR)에 대해 다루어 보고자 한다.
▶ Reference:
[1]. 고려대학교 강필성 교수님 강의자료
https://github.com/pilsung-kang/Business-Analytics-IME654-/tree/master/02%20Kernel-based%20Learning
[2]. 위키백과
https://ko.wikipedia.org/wiki/%EC%84%9C%ED%8F%AC%ED%8A%B8_%EB%B2%A1%ED%84%B0_%EB%A8%B8%EC%8B%A0
[3]. Margin 구하는 과정 참고자료
[4]. SVM 참고자료
https://zephyrus1111.tistory.com/211
[5]. Lagrangian Method 참고자료
https://psystat.tistory.com/103
[6]. Quadratic Programming 참고자료
[7]. Kernel function 참고자료
'Machine Learning > Kernel Based Learning' 카테고리의 다른 글
| Support Vector Regression(SVR) (0) | 2023.01.16 |
|---|
