Gaussian Process Regression(GPR)에 대해 알기 전에 필요한 기본적인 개념은 [Gaussian Process (1): Mathematical Basics]에서 다루었습니다. 본 글에서는 본격적으로 Gaussian Process Regression(GPR)에 대해 다루어 보고자 합니다.
0. Definition
Gaussian Process Regression(GPR)는 Gaussian Process(GP)의 특성을 이용한 Nonparametric Bayesian Regression(비모수 베이지안 회귀) 방법입니다.
GPR은 크게 다음 2가지의 관점에서 살펴볼 수 있는데 본 글에서는 Function-space view 관점에서 살펴볼 것입니다.
- Weight-space view
- Function-space view
1. Basic Idea
본 Section 1에서 다루는 내용은 GPR의 기본적인 아이디어입니다.
훈련 데이터셋 $D = \{(x_i,y_i)\}^n_{i=1}$이 주어진 경우, regression(회귀)에서의 주 목적은 데이터를 가장 잘 적합하는 unknown function $f: X \to Y$를 찾는 것이 목적입니다. 전통적인 비선형 회귀 모델의 경우, 오직 하나의 함수 $f$만을 찾습니다. 하지만, 관측된 데이터를 가장 잘 설명하는 함수 $f$가 한 개 이상 존재할 수도 있습니다.

[Figure 1]을 참조하면(그림 출처:PyMC3), 관측된 데이터셋(black point)을 설명하는 함수 $f$가 여러개가 존재하는 것을 확인할 수 있습니다.
Question: 데이터를 가장 잘 설명하는 함수 $f$를 어떻게 여러개 찾을 수 있을까?
만약, 함수 $f$가 무한차원의 다변량 정규분포($p \to \infty$)를 따른다면, 이 분포로부터 우리는 무한개의 함수를 샘플링할 수 있습니다(사전분포(Prior Distribution): $f \sim N_{\infty} (\mu, \Sigma)$ → $f \sim GP(m(x), k(x,x'))$).
사전분포에서는 관측된 데이터 없이 입력값 $X$에 대해 기대되는 산출값 $f$를 표현하였습니다.
관측값이 주어진 경우, 우리는 관측된 데이터를 이용해 함수 $f$를 적합할 수 있습니다. 즉, 우리는 Bayesian Theroem을 응용해 관측된 데이터와 함께 사전분포는 사후분포(Posterior Distribution)로 업데이트됩니다($f_*|f,x = p(f) \times p(x|f)$).
[Bayesian Theorem]
- $\text{Posterior Distribution} \propto \text{Prior Distirbution} \times \text{Likelihood}$
- $P(A|B) = \dfrac{P(B|A)P(A)}{P(B)} \propto P(B|A)P(A)$
- $P(A|B)$: posterior probability
- $P(B|A)$: likelihood
- $P(A)$: prior probability
- $P(B)$: marginal probability
새로운 관측값 $X_{new}$이 또 관측된 경우, 현재 사후분포는 사전분포로 사용하고 $X_{new}$와 함께 사전분포는 다시 사후분포($f_{new}|f_*,x_{new},x$)로 업데이트 됩니다. 이와 같은 과정을 반복하면, 데이터에 적합한 여러개의 함수를 찾을 수 있습니다.
지금까지 GPR의 기본적인 아이디어에 대해 살펴보았습니다. 본 Section 2에서는 GPR의 전반적인 내용을 수식을 통해 알아보고자 합니다.
2. Gaussian Process Regression(GPR)
[Prior Distribution: Gaussian Process or Multivarite Gaussian Distribution]
함수 $f$의 분포로 Gaussian Process(GP)로 설정하였습니다.
다르게 이야기하면, GP는 함수에 대한 확률분포입니다.
$$f(x) \sim GP(m(x), k(x,x'))$$
- $m(x)$: mean function
- $k(x,x') = E[(f(x)-m(x))(f(x')-m(x'))]$: covariance function
보편적으로 $m(x)=0$으로 설정합니다.
만약, $f$가 평균함수 $m(x)$가 0인 GP를 따르는 경우,
$n$차원의 함수 $f(x) = \begin{bmatrix} f(x_1) \\ f(x_2) \\ \vdots \\ f(x_n) \end{bmatrix} \in \mathbb{R}^n$은 $n$차원의 다변량 정규분포를 따릅니다.
$$ \begin{bmatrix} f(x_1) \\ f(x_2) \\ \vdots \\ f(x_n) \end{bmatrix} \sim N_n(0, \begin{bmatrix} k(x_1, x_1) & k(x_1,x_2) & \cdots & k(x_1,x_n) \\ k(x_2,x_1) & k(x_2,x_2) & \cdots & k(x_2,x_n) \\ \vdots& \dots & \vdots \\ k(x_n, x_1) & k(x_n, x_2) & \cdots & k(x_n,x_n) \end{bmatrix})$$
[Example]
간단한 예시로 $ y = 0.5 sin(3x)$에서 샘플링한 20개의 샘플($X = x_1, x_2, \cdots, x_{20}$)에 대한 데이터입니다([Figure 2]).

$$ f = \begin{bmatrix} f(x_1) \\ f(x_2) \\ \vdots \\ f(x_{20}) \end{bmatrix} \sim N(0, \begin{bmatrix} k(x_1, x_1) & k(x_1,x_2) & \cdots & k(x_1,x_{20}) \\ k(x_2,x_1) & k(x_2,x_2) & \cdots & k(x_2,x_{20}) \\ \vdots& \dots & \vdots \\ k(x_{20}, x_1) & k(x_{20}, x_2) & \cdots & k(x_{20},x_{20}) \end{bmatrix}) = N(0,K(X,X)) \tag{1}$$
커널 함수 $K(\cdot, \cdot)$은 RBF kernel를 사용하였습니다.
$$k(x, x') = \sigma^2 exp( -\dfrac{||x-x'||^2}{2 l^2})$$
- parameter: lengthscale $l$, variance $\sigma^2$
[Figure 3]은 사전 분포인 식 $(1)$로부터 2개의 함수 $f_1$(blue), $f_2$(orange)를 샘플링한 결과입니다.


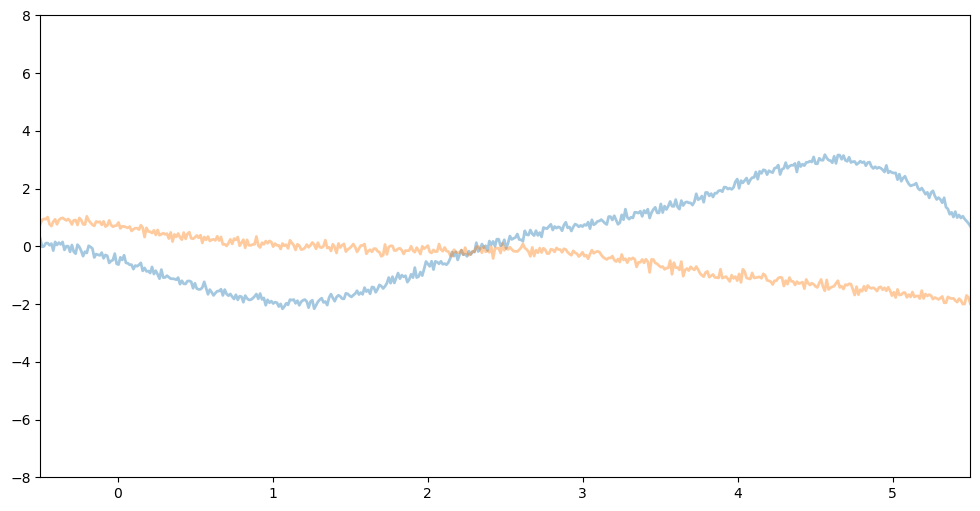
[Figure 3]의 3개의 그림을 확인해보면 모두 서로 다른 모양을 갖는 함수임을 알 수 있습니다. 왼쪽 그림을 기준으로 가운데 그림은 lengthscale인 $l$값을 증가시켰을 경우, 오른쪽 그림은 변동성인 $\sigma^2$ 값을 감소시킨 경우입니다. 즉, $l$
값을 증가시킬수록 $\sigma^2$ 값을 작게 둘 수록 함수의 형태는 smooth해짐을 알 수 있습니다.
또한, 커널을 만약 polynomial($k(x,x') = \sigma^2(bias + x \cdot x')^d$) 혹은 linear($k(x,x') = \sigma^2 x \cdot x'$)을 이용한 경우는 또 다른 함수의 형태가 보입니다.
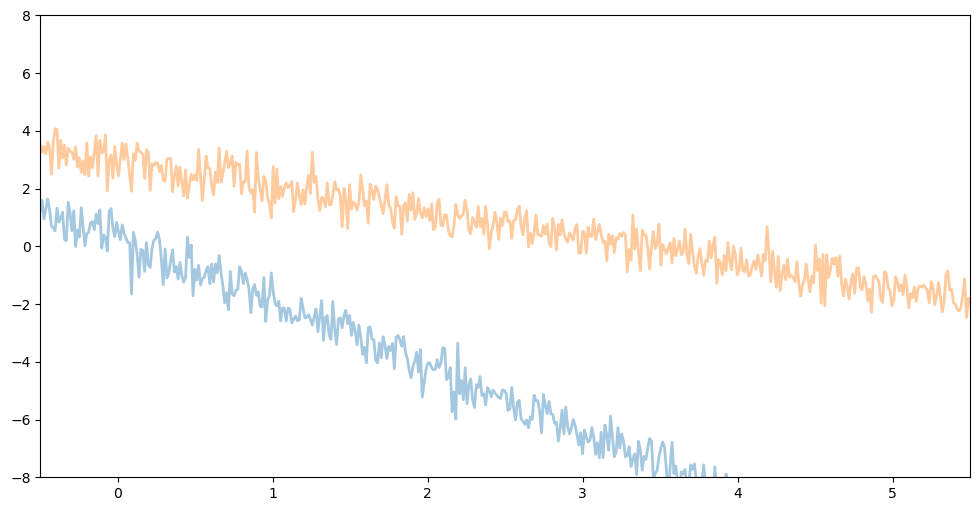

우리는 GPR의 경우, 커널 함수 $K$에 의해 함수의 형태가 달라지는 것을 확인할 수 있습니다.
따라서, 데이터의 형태에 따라 적절한 커널함수를 사용하는 것이 중요합니다.
[Update: Posterior Distribution]
만약 새로운 데이터 $x_*$이 입력된 경우, 관측된 데이터 $f=(f(x_1),f(x_2),\cdots, f(x_n))$와 새로운 데이터 $f_* = f(x_*)$의 결합정규분포를 정의할 수 있습니다.
$$ \begin{bmatrix} f(x_1) \\ f(x_2) \\ \vdots \\ f(x_n) \\ f(x_*) \end{bmatrix} \sim N(0, \begin{bmatrix} k(x_1, x_1) & k(x_1,x_2) & \cdots & k(x_1,x_n) & k(x_1,x_*) \\ k(x_2,x_1) & k(x_2,x_2) & \cdots & k(x_2,x_n) & k(x_2, x_*) \\ \vdots& \dots & \vdots \\ k(x_n, x_1) & k(x_n, x_2) & \cdots & k(x_n,x_n) & k(x_n, x_*)\\ k(x_*,x_1) & k(x_*,x_2) & \cdots & k(x_*, x_n) & k(x_*, x_*) \end{bmatrix}) \tag{2}$$
식 $(2)$를 더 간단하게 다음과 같이도 표현 가능합니다($f(X) = (f(x_1),f(x_2),\cdots,f(x_n))^T$).
$$ \begin{bmatrix} f(X) \\ f(x_*) \end{bmatrix} \sim N(0, \begin{bmatrix} K(X,X) & K(X,x_*) \\ K(x_*,X) & k(x_*, x_*) \end{bmatrix}) \tag{3}$$
우리의 주 목적은 기존의 관측치 $X$에 더해 새로운 관측치 $x_*$가 주어졌을 때 기존의 함수(사전 분포) $f$를 새로운 함수(사후 분포) $f_*$로 업데이트 하는 것입니다.
식 $(3)$을 조건부 분포로 변환하면 다음과 같습니다(사후 분포).
$$f_*|x_*,X,f \sim N(\mu_*, \sigma^2_*)$$
- $\mu_* = K(x_*,X)K(X,X)^{-1}f$
- $\sigma_* = k(x_*,x_*) - K(x_*,X)K(X,X)^{-1}K(X,x_*)$
지금까지는 측정 오차(measurement error, $\epsilon$)가 없는 경우에 대해 다루었습니다($y=f(x)$). 하지만, 실제 데이터에서는 측정 오차가 존재하는 경우가 대다수입니다.
$$y=f(x)+\epsilon, \epsilon \sim N(0, \sigma^2_n)$$
이와 같은 경우, 주변분포 및 결합분포와 조건부 분포는 다음과 같습니다.
[Prior Distribution]
$$ \begin{bmatrix} f(x_1) \\ f(x_2) \\ \vdots \\ f(x_n) \end{bmatrix} \sim N_n(0, \begin{bmatrix} k(x_1, x_1) + \sigma^2_n & k(x_1,x_2) & \cdots & k(x_1,x_n) \\ k(x_2,x_1) & k(x_2,x_2) + \sigma^2_n & \cdots & k(x_2,x_n) \\ \vdots& \dots & \vdots \\ k(x_n, x_1) & k(x_n, x_2) & \cdots & k(x_n,x_n) + \sigma^2_n \end{bmatrix})$$
커널 함수의 대각 원소에 $\sigma^2_n$이 추가되었다는 것을 확인할 수 있습니다.
$$ \begin{bmatrix} f(X) \\ f(x_*) \end{bmatrix} \sim N(0, \begin{bmatrix} K(X,X) + \sigma^2_n I_n& K(X,x_*) \\ K(x_*,X) & K(x_*, x_*) \end{bmatrix})$$
[Posterior Distribution]
$$f_*|x_*,X,f \sim N(\mu_*, \sigma^2_*)$$
- $\mu_* = K(x_*,X)(K(X,X)+\sigma^2_nI_n)^{-1}f$
- $\sigma_* = k(x_*,x_*) - K(x_*,X)(K(X,X)+\sigma^2_nI_n)^{-1}K(X,x_*)$
이전에 살펴보았던 예시를 통해 사후분포로 업데이트된 결과를 보여주고자 합니다.

빨간색 선(red line)이 사후 평균 $\mu_*$, 하늘색 음영(blue area)이 사후 표준편차 $\sigma_*$입니다.
GPR의 가장 큰 특징은 불확실성(uncertatinty, $\sigma_*$)를 다룰 수 있다는 점입니다. 관측된 데이터 ×가 존재하는 부분은 상대적으로 불확실성이 적은 반면, 관측된 데이터가 존재하지 않은 부분은 불확실성이 큰 것을 [Figure 5]를 통해 확인할 수 있습니다.
GPR이 불확실성을 다룰 수 있다는 큰 특징이 존재하지만 커널 계산 비용에 있어서 큰 비용이 든다는 단점이 존재합니다.
지금까지 Gaussian Process Regression(GPR)에 대한 이론을 설명하였습니다.
Gaussian Process Regression 혹은 Classification을 직접 코드로 구현해서 연습해 보고 싶으신 경우,
pytorch로 구현된 pyro 혹은 tensorflow로 구현된 gpflow를 이용하시면 도움이 될 것입니다.
[Pyro]
Gaussian Processes — Pyro Tutorials 1.8.6 documentation
Introduction Gaussian Processes have been used in supervised, unsupervised, and even reinforcement learning problems and are described by an elegant mathematical theory (for an overview of the subject see [1, 4]). They are also very attractive conceptually
pyro.ai
[GPflow]
gpflow.optimizers — GPflow 2.9.0 documentation
step_callback (Union[Callable[[int, Sequence[Variable], Sequence[Tensor]], None], Monitor, None]) – If not None, a callable that gets called once after each optimisation step. The callable is passed the arguments step, variables, and values. step is the
gpflow.github.io
▶ 참고자료
[논문]: An Intuitive Tutorial to Gaussian Processes Regression
[강의자료]: '최성준님의 Bayesian Deep Learning '
'Gaussian Process > Gaussian Process' 카테고리의 다른 글
| Gaussian Process(1): Mathematical Basics (0) | 2023.12.14 |
|---|
