1. CNN 간략하게 설명
Convolution이란?
Convolution Filter(kernel)를 이용하여 image를 순회하는 dot product를 계산하고, 기존의 데이터로부터 filter를 이용하여 새로운 tensor(=activation map)을 만드는 것.
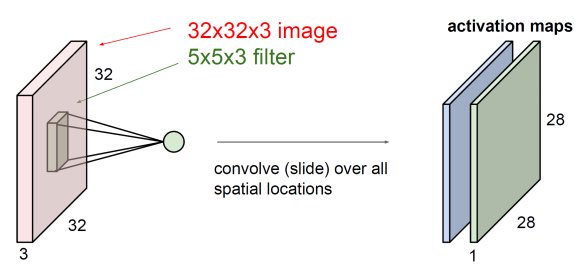
filter의 깊이를 receptive field라고 하는데 receptive field가 깊을수록 더 깊은 layer가 나오게 되고, neural network의 깊은 곳에서 더 깊은 receptive field가 발생하고, 얕은 곳에서는 얕은 receptive field 발생한다. Convolution 연산의 큰 특징 중 하나가 weight sharing이다.
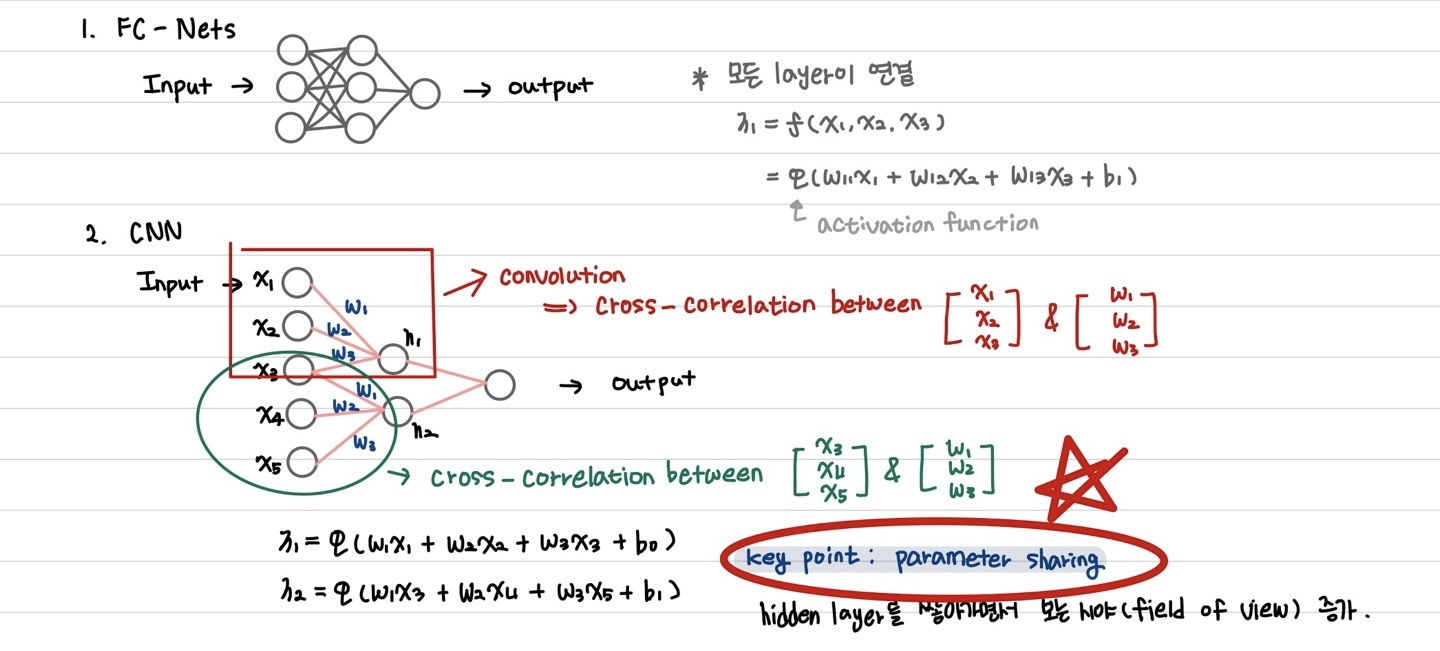
Weight Sharing의 효과
- 학습할 parameter의 수 감소
- overfitting의 문제 해결
Convolution Filter의 효과
- local한 feature를 잘 뽑아낼 수 있음
- down-sampling에 대한 효과를 얻을 수 있음
CNN
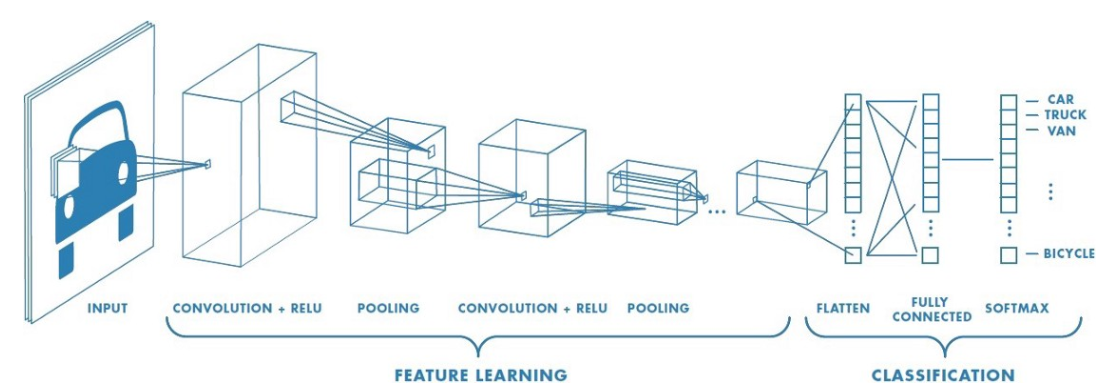
CNN은 이미지를 작은 구역으로 나누어 지역적인 정보를 계속 취합하는 식으로 작동한다. CNN은 크게 Feature Learning 단계와 Classification 단계로 나눌 수 있다. Feature Learning 단계에서는 convolution 연산과 pooling 연산을 반복적으로 수행한다. convolution은 각각의 구역으로부터 정보를 추출하고 pooling 연산은 추출된 정보 중 태스크 수행(이미지 분류 등)에 중요한 정보만을 남기는 작업을 한다. Classification 단계에서는 주로 Fully Connected(MLP)을 사용하는데 이미지 task에서 MLP를 이용한 방법론은 모든 node와 layer가 이어져 있기 때문에 parameter의 수가 기하급수적으로 증가한다. 또한, image에서 pixel이 조금이라도 틀어지면 기존의 parameter가 변질되기 때문에 성능이 안 좋아진다는 단점이 있다. 결론적으로 image에서 important feature를 추출하는 게 중요하다.
GCN도 CNN과 마찬가지로 태스크 수행에 있어 가장 중요한 정보를 그래프에서 뽑아내는 것이 목표이다.
- GCN은 필터를 그래프에 통과시켜 그래프 내에서 중요한 노드와 엣지로부터 정보를 취합한다.
- CNN에서 convolution filter를 사용하면 image로부터 어떤 feature들을 뽑아내고 activation map이 update가 되면서 연산이 진행되는데 이러한 과정을 GCN에서도 동일하게 적용한다.
2. GCN Formulation
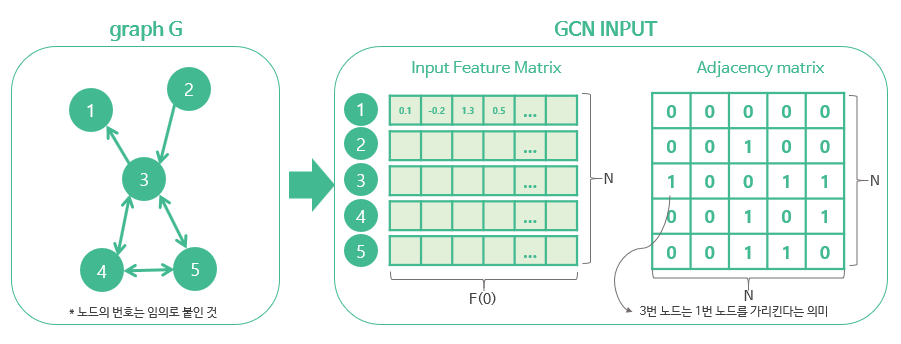
G(Graph) = (V, E)가 주어질 때 GCN은 다음을 input으로 받는다.
- node(input) feature matrix: size=N*F(0) (N: node의 개수, F(0): 각 node에 있는 input feature dimension)
- graph structure에 대한 표현: size= N*N, 그래프 G의 인접성 행렬(adjacency matrix) 등을 사용한다.
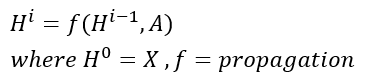
- 각 layer H는 N*F(i) Feature Matrix 의미한다.(각 행이 node에 대한 representation)
- 각각의 layer의 feature들은 propgation rule f에 따라 취합되어 다음 layer로 넘어간다.
-> 다양한 GCN의 변형들은 결국 propgation rule을 어떻게 정하느냐에 따라 달라지게 된다.
- CNN에서 첫 번째 layer가 edge, 색깔과 같은 기본적인 특성을 포착하고 뒷 layer로 갈수록 추상적인 feature를 포착하는 것처럼 GCN에서도 나중 layer로 갈수록 graph에서 더욱 추상적인 특성을 뽑아내게 된다.
2.1 Simple Propgation Rule
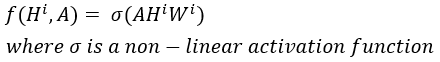
- W는 i번째 layer의 weight matrix로, F(i) * F(i+1)의 dimension을 가진다.(feature의 차원을 변화)
- 한 layer의 weight는 graph에 있는 node 전체에 대해 공유한다는 점에서 CNN의 convolution 연산과 유사하다.
2.2 How to update hidden states in GCN?
node feature matrix를 update하여 task 수행한다.
- 각 node들이 갖는 feature가 update 되는 것이 목표라면, convolution layer를 이용하여 feature update 수행한다.
- convolution layer는 local한 부분의 feature들을 모아서 연산했다면, 이와 동일한 방식으로 graph도 주변에 있는 부분들로 update를 하는 것이다.
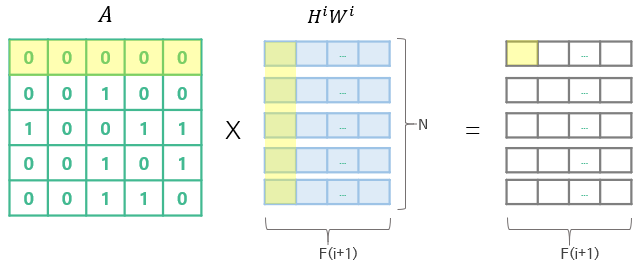

- 새로 만들어진 matrix에 대해 인접성 행렬을 곱하면, 결과로 나오는 matrix의 (i, j)의 값은 node i와 연결된 모든 node의 j번째 행렬 값의 합으로 구해진다. (즉, 각각의 node와 연결되어 있는 노드의 정보를 모아 feature update)
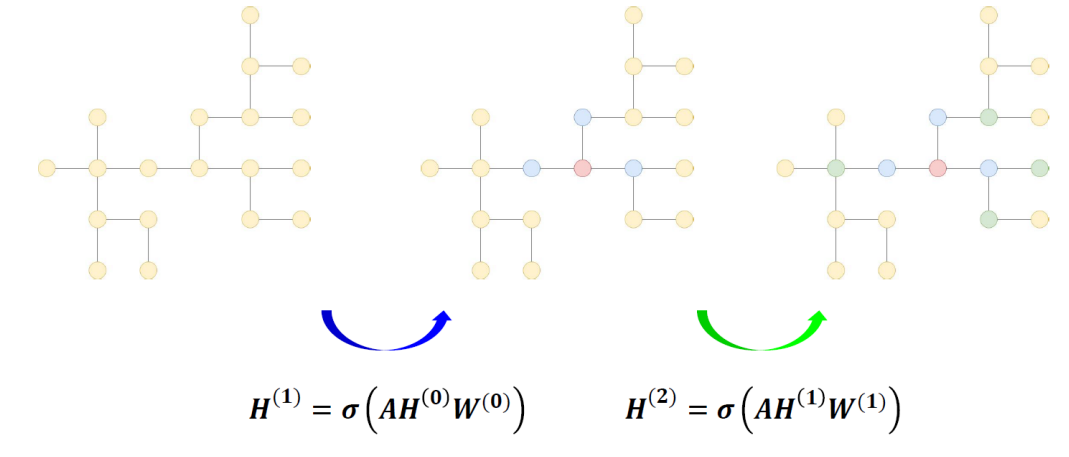
다른 그림을 통해서도 설명을 해보고자 한다.(W: weight, l: l번째 Layer, H: Hidden State(=각 layer를 거치고 난 뒤의 node feature matrix))
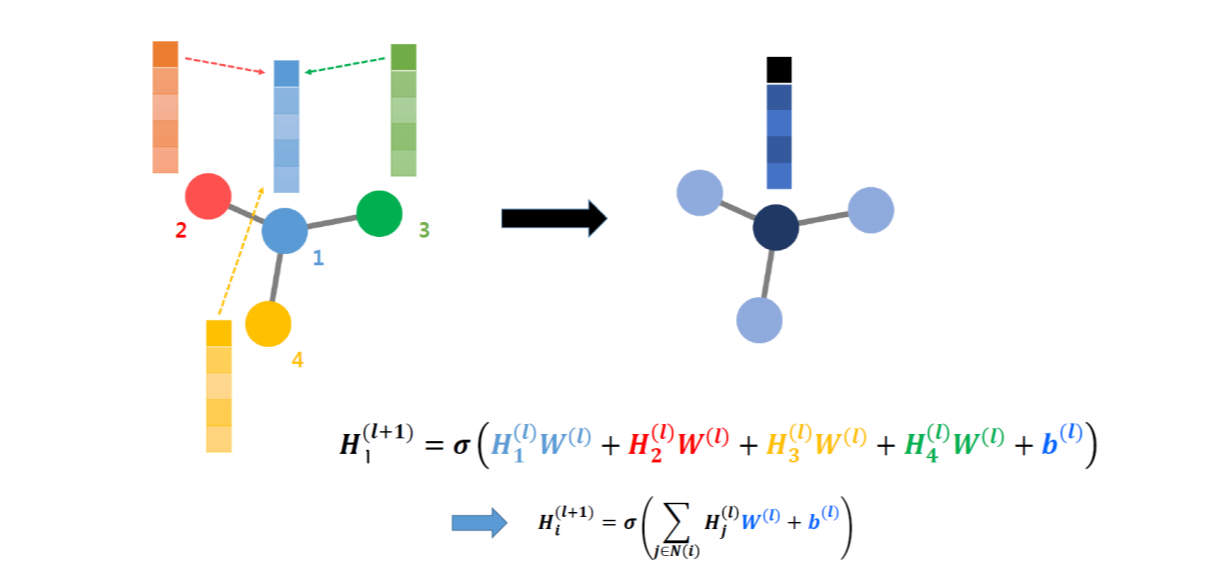
node 1에 대해 풀어서 설명하면, node 1의 l번째 node feature matrix에 l번째 weight 행렬을 곱한 것이다.
node의 (l+1)번째 node feature matrix를 나타낸 것인데, 이는 node 1과 인접한 모든 node들의 node feature matrix에 각 weight를 곱하고 bias를 더하여 activation function을 씌어주어 update 한 것이다.
이는 모든 node의 weight가 다 동일하기 때문에 weight sharing을 가능하게 한다.
따라서, 이 업데이트 과정은 앞에서 반복적으로 설명했던 것처럼 convolution 연산과 같이 local한 정보를 이용하고, weight sharing을 한다는 특징을 가지기 때문에 GCN이라고 부르는 것이다.
- 각 node들을 업데이트하려면 해당 node의 인접한 node들의 정보, 또 그 node의 인접한 node의 정보...., 이런식으로 연쇄적으로 연결되어 있기 때문에, 이러한 connectivity의 정보를 갖고 있는 Adjacency Matrix(인접 행렬)를 이용하여 구할 수 있다.
- 각 node의 n번째 인접한 node의 연결 여부를 알기 위해서는 간단하게 Adajency Matrix를 n번 곱하면 된다.
- 그러면, 간단한 행렬 연산으로 convolution 연산 수행이 가능하다.
3. Problem
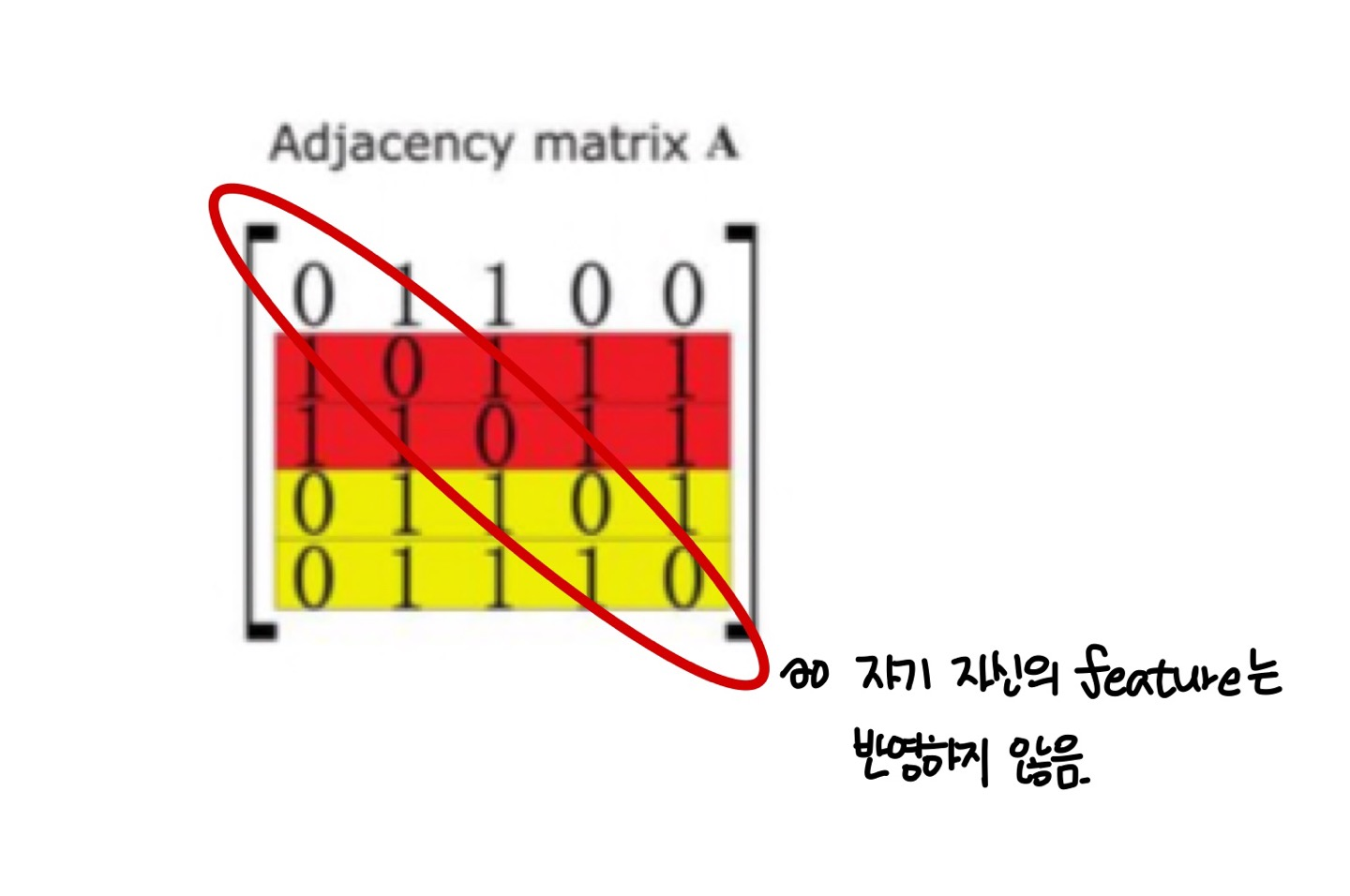
1. 자기 자신의 feature은 특성을 모을 때 반영되지 않는다.
- 스스로 가리키는 self-loop을 가지고 있는 노드만이 feature를 취합할 때 자신의 정보를 반영한다.
- 노드의 feature를 만드는 데에 있어 자신의 정보를 포함하지 않는 것은 직관적으로 생각해도 이상하다.
2. 연결이 많이 되어 있는 node는 feature representation에 큰 값을 가지고, 연결이 적은 node는 값이 작아진다.
- 이로 인해, 많은 node와 연결되어 있는 경우 exploding gradient 발생
- 연결이 저근 node의 경우, vanishing gradient 발생
4. Solution
A. self-loop 포함하기
- 각각의 node에 대해 self-loop를 주어, adajency matrix A의 대각 원소는 1의 값을 가지게 한다.
- 이렇게 하면, feature를 취합할 때 항상 자신의 특성을 고려할 수 있게 된다.
B. Feature Representation 정규화하기
- node의 연결성에 대해 계산된 feature를 정규화(normalization) 함으로써 back-propgation을 안정화 할 수 있음
- node의 연결성을 차원(degree)이라고 부르는데, adajency matrix(A)의 차원(D)에 대한 역행렬을 곱해줌으로써 정규화 할 수 있음.
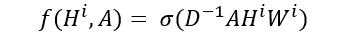
- Degree Matrix: node에 연결된 node의 수(또는 Edge의 수)
5. Readout = Permutation Invariance
- 같은 graph 구조를 갖지만, 위치가 달라짐으로 인해 Adajency Matrix가 달라지게 되는 error가 발생한다.
- graph structure가 어떠하든 상관 없이 같은 위상을 갖는 graph라면 같은 결과를 내야 한다.
- 이 error를 방지하기 위하여 Readout 또는 Permutation Invaraince를 사용해야 한다.
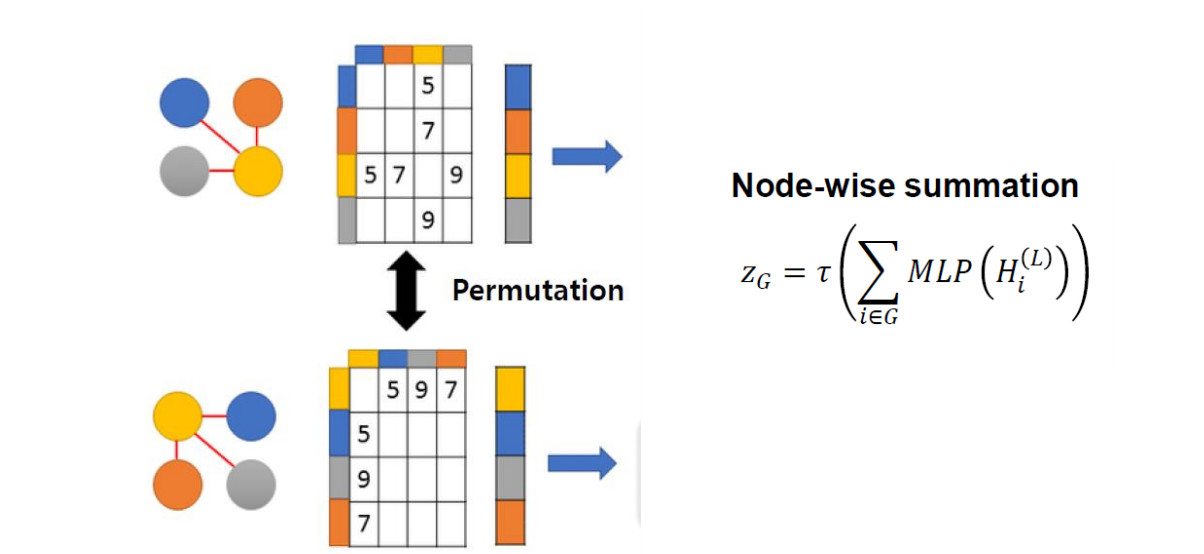
- l번째 node feature matrix에 대해 MLP(=fully connected)를 씌어주어 sum을 한 후 activation을 씌우면 같은 위상에 대해서 다른 node 위치를 갖는 graph에 대해 동일한 결과를 낼 수 있다.
6. GCN Structure
Input data: Node Feature Matrix(X) & Adajency Matrix(A)
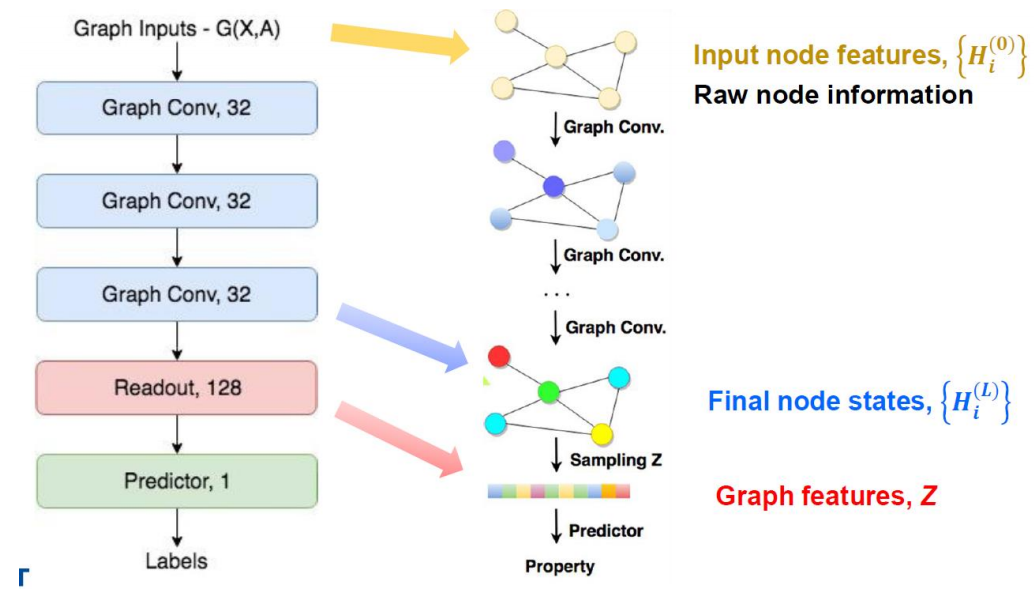
- Node Feature Matrix인 X와 Adajency Matrix인 A를 갖는 graph를 input 하였을 때, 원하는 만큼의 convolution 연산을 거치고 Readout을 적용한 후 fully connected layer를 거친 후 우리가 원하는 결과를 얻는다.
- Training: output과 실제 true label 혹은 true value와의 loss를 구하고 그 loss를 minimize하게끔 weight update
- Convolution layer에서는 각 node들의 node feature들에 대한 weight update
7. Advanced Techniques of GCN
7.1 Inception
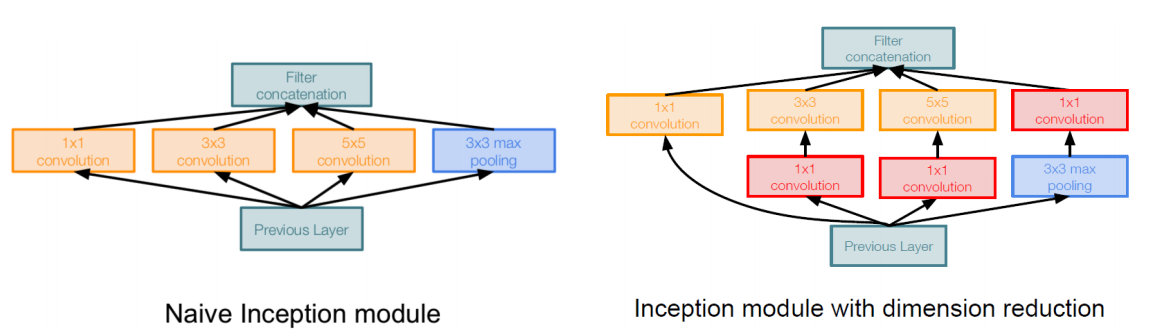
- 하나의 filter만 적용시키는 것이 아니라 여러 size의 filter들을 병렬로 적용한 후에 concat시켜서 다음 layer를 만드는 모듈이다.
- depth가 깊어지는 단점을 보완하기 위해 1 by 1 filter를 적용시켜서(->dimension reduction) computation efficiency를 향상시킨다.
Inception 모듈을 GCN에 적용
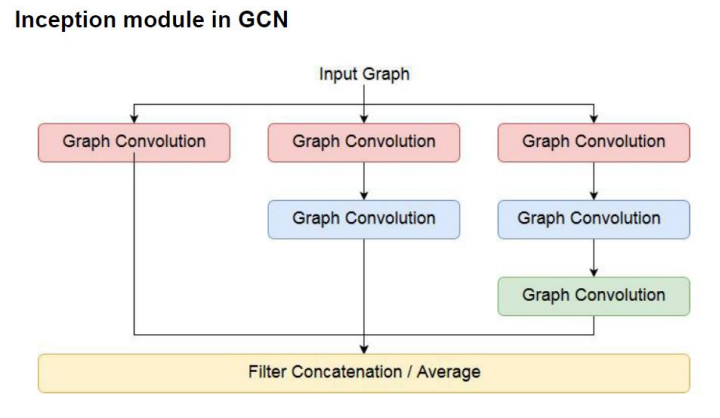
- inception 모듈은 다양한 크기의 filter를 사용하는 것이 핵심이다.
- 이를 GCN에 적용시키면 다양한 hop의 인접한 node들의 feature를 사용하는 것으로 적용시킬 수 있다.
- 다양한 hop 생성방법은 Adajency Matrix를 계속해서 곱해주면 된다.
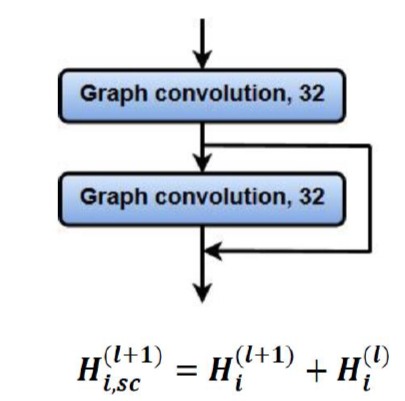
7.2 Skip Connection
- Resnet에서 사용된 Skip Connection
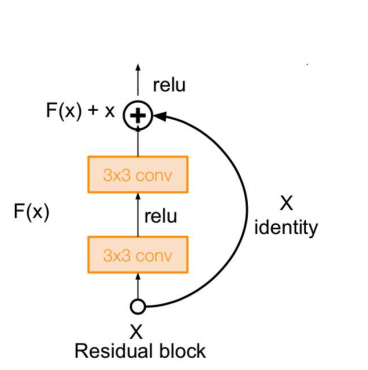
- Neural Network의 depth가 깊어질수록 성능이 오히려 감소하는 현상이 발생한다. 이를 skip 할 수 있는 모듈을 만들어주어 성능이 오로지 우상향 할 수 있게 만들어준다.
7.3 Attention
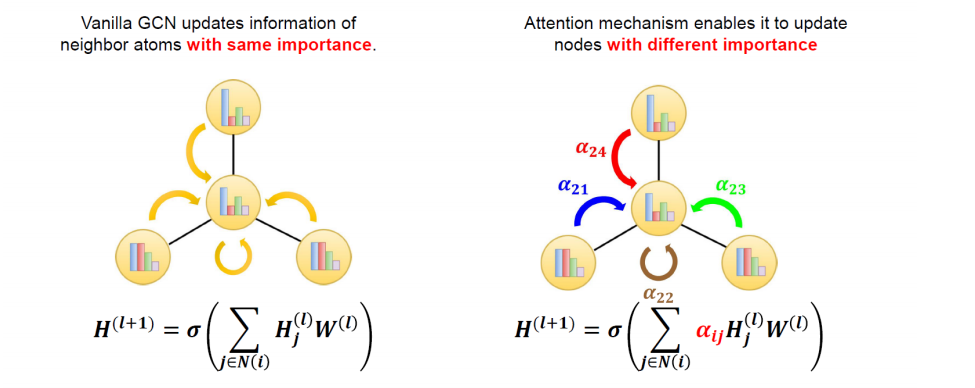
- 기존의 GCN은 자기 자신 node를 포함하여 인접한 node의 feature를 합하여 update 진행한다. 이때 각 인접한 node의 feature를 동일한 가중치로 여기고 합한다.
- Attention을 적용한 GCN은 동일한 가중치를 주지 말고, 특정 비율로 합하여 업데이트 하자는 것이다.
- 가중치의 값은 각 노드끼리의 correlation으로 정해진다.
8. 2D Convolution vs. Graph Convolution
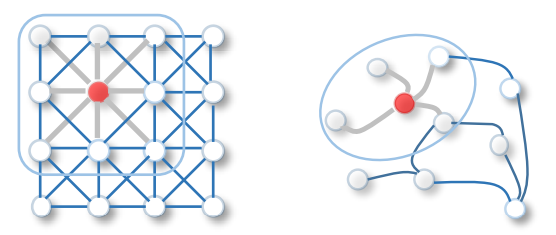
공통점
모두 지역적인 정보를 취합해 feature를 고도화하는 과정
차이점
- 2D convolution은 특정 pixel(혹은 위치)과 인접해 있는 지역의 정보를 모은다.
- Graph Convolutioin은 node와 연결되어 있는 node들의 정보를 모은다.
- 이때 정보를 취합하는 방법(Weight matrix)은 한 layer 안에서 모든 위치 혹은 노드에 대해 공유한다.
참고자료: https://www.youtube.com/watch?v=YL1jGgcY78U
'Graph(Graph Neural Network)' 카테고리의 다른 글
| Semi-Supervised Classification With Graph Convolutional Networks (0) | 2022.09.19 |
|---|---|
| Graph Convolutional Networks for Text Classification (0) | 2022.09.18 |
| Semi-Supervised Classification With Graph Convolutional Neworks (0) | 2022.09.18 |
| Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting (0) | 2022.09.09 |
| Graph Structure (0) | 2022.09.09 |



