2024년 6월에 푼 프로그래머스 코딩문제("코딩테스트 공부 목적")
본 글은 프로그래머스와 백준에서 푼 문제를 정리한 글입니다.
1. [백준: 다이나믹 프로그래밍] 연속합(정답률: 36.810%)
[문제]
n개의 정수로 이루어진 임의의 수열이 주어진다. 우리는 이 중 연속된 몇 개의 수를 선택해서 구할 수 있는 합 중 가장 큰 합을 구하려고 한다. 단, 수는 한 개 이상 선택해야 한다.
예를 들어서 10, -4, 3, 1, 5, 6, -35, 12, 21, -1 이라는 수열이 주어졌다고 하자. 여기서 정답은 12+21인 33이 정답이 된다.
[입력]
첫째 줄에 정수 n(1 ≤ n ≤ 100,000)이 주어지고 둘째 줄에는 n개의 정수로 이루어진 수열이 주어진다. 수는 -1,000보다 크거나 같고, 1,000보다 작거나 같은 정수이다.
[출력]
첫째 줄에 답을 출력한다.
[코드]
n = int(input())
array = list(map(int, input().split()))
for i in range(n-1):
array[i+1] = max(array[i]+array[i+1], array[i+1])
print(max(array))2. [백준: 그래프 이론] 토마토(7576)(정답률: 36.806%)
[문제]
철수의 토마토 농장에서는 토마토를 보관하는 큰 창고를 가지고 있다. 토마토는 아래의 그림과 같이 격자 모양 상자의 칸에 하나씩 넣어서 창고에 보관한다.
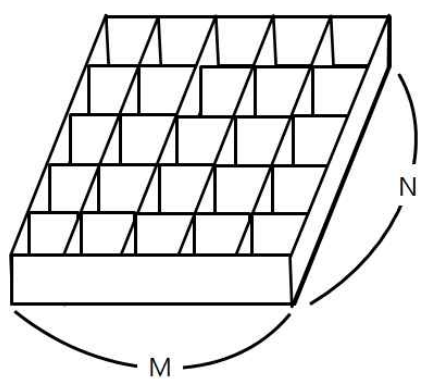
창고에 보관되는 토마토들 중에는 잘 익은 것도 있지만, 아직 익지 않은 토마토들도 있을 수 있다. 보관 후 하루가 지나면, 익은 토마토들의 인접한 곳에 있는 익지 않은 토마토들은 익은 토마토의 영향을 받아 익게 된다. 하나의 토마토의 인접한 곳은 왼쪽, 오른쪽, 앞, 뒤 네 방향에 있는 토마토를 의미한다. 대각선 방향에 있는 토마토들에게는 영향을 주지 못하며, 토마토가 혼자 저절로 익는 경우는 없다고 가정한다. 철수는 창고에 보관된 토마토들이 며칠이 지나면 다 익게 되는지, 그 최소 일수를 알고 싶어 한다.
토마토를 창고에 보관하는 격자모양의 상자들의 크기와 익은 토마토들과 익지 않은 토마토들의 정보가 주어졌을 때, 며칠이 지나면 토마토들이 모두 익는지, 그 최소 일수를 구하는 프로그램을 작성하라. 단, 상자의 일부 칸에는 토마토가 들어있지 않을 수도 있다.
[입력]
첫 줄에는 상자의 크기를 나타내는 두 정수 M,N이 주어진다. M은 상자의 가로 칸의 수, N은 상자의 세로 칸의 수를 나타낸다. 단, 2 ≤ M,N ≤ 1,000 이다. 둘째 줄부터는 하나의 상자에 저장된 토마토들의 정보가 주어진다. 즉, 둘째 줄부터 N개의 줄에는 상자에 담긴 토마토의 정보가 주어진다. 하나의 줄에는 상자 가로줄에 들어있는 토마토의 상태가 M개의 정수로 주어진다. 정수 1은 익은 토마토, 정수 0은 익지 않은 토마토, 정수 -1은 토마토가 들어있지 않은 칸을 나타낸다.
토마토가 하나 이상 있는 경우만 입력으로 주어진다.
[출력]
여러분은 토마토가 모두 익을 때까지의 최소 날짜를 출력해야 한다. 만약, 저장될 때부터 모든 토마토가 익어있는 상태이면 0을 출력해야 하고, 토마토가 모두 익지는 못하는 상황이면 -1을 출력해야 한다.
[코드]
M,N = map(int, input().split())
matrix = []
for _ in range(N):
matrix.append(list(map(int, input().split())))
adj = []
for i in range(N):
for j in range(M):
if matrix[i][j]==1:
adj.append([i,j])
def go_stack(matrix,adj1,directions):
adj2 = []
while adj1:
cx,cy = adj1.pop()
for dx,dy in directions:
if (cx+dx >= 0) and (cx + dx <= N-1) and (cy+dy>=0) and (cy+dy<=M-1):
if matrix[cx+dx][cy+dy]==0:
adj2.append([cx+dx,cy+dy])
matrix[cx+dx][cy+dy] = 1
else:
continue
return adj2,matrix
def tomato(matrix, adj):
count = 0
directions = [[-1,0],[1,0],[0,-1],[0,1]]
while adj:
adj, matrix = go_stack(matrix,adj,directions)
if adj:
count += 1
for i in range(N):
for j in range(M):
if matrix[i][j] == 0:
return -1
return count
print(tomato(matrix, adj))3. [백준: 다이나믹 프로그래밍] 다리 놓기(1010번)(정답률: 47.928%)
[문제]
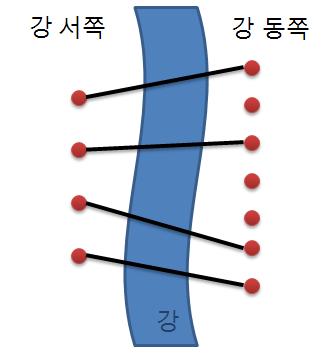
재원이는 한 도시의 시장이 되었다. 이 도시에는 도시를 동쪽과 서쪽으로 나누는 큰 일직선 모양의 강이 흐르고 있다. 하지만 재원이는 다리가 없어서 시민들이 강을 건너는데 큰 불편을 겪고 있음을 알고 다리를 짓기로 결심하였다. 강 주변에서 다리를 짓기에 적합한 곳을 사이트라고 한다. 재원이는 강 주변을 면밀히 조사해 본 결과 강의 서쪽에는 N개의 사이트가 있고 동쪽에는 M개의 사이트가 있다는 것을 알았다. (N ≤ M)
재원이는 서쪽의 사이트와 동쪽의 사이트를 다리로 연결하려고 한다. (이때 한 사이트에는 최대 한 개의 다리만 연결될 수 있다.) 재원이는 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수만큼 (N개) 다리를 지으려고 한다. 다리끼리는 서로 겹쳐질 수 없다고 할 때 다리를 지을 수 있는 경우의 수를 구하는 프로그램을 작성하라.
[입력]
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
[출력]
각 테스트 케이스에 대해 주어진 조건하에 다리를 지을 수 있는 경우의 수를 출력한다.
[코드]
※ 코드 풀이
- 특징 1) $N \leq M$이기 때문에 최대 만들 수 있는 다리의 개수는 $N$개 입니다.
- 특징 2) 순서를 고려하지 않습니다. → $(1,3,4)$나 $(1,4,3)$을 다른 것으로 보지 않으며 문제의 조건에 맞는 경우의 수도 $(1,3,4)$입니다.
특징 1)과 특징 2)의 속성을 모두 고려할 수 있는 성질이 조합입니다.
$$nCr = \dfrac{n!}{r! (n-r)!}$$
본 코드는 조합의 두 가지 성징을 이용하여 풀었습니다.
- ${}_{n+1}C_{r+1} = {}_{n}C_r + {}_{n}C_{r+1}$
- ${}_{n}C_{0} = {}_{n}C_{n} = 1$
def combination(n,r, d):
if d[n][r]>0:
return d[n][r]
if (n==r) or (r==0):
d[n][r] = 1
return d[n][r]
d[n][r] = combination(n-1,r-1,d)+combination(n-1,r,d)
return d[n][r]
T = int(input())
site = []
for _ in range(T):
site.append(list(map(int, input().split())))
d = [[0 for i in range(30)] for j in range(30)]
for n,m in site:
combination(m,n,d)
print(d[m][n])4. [백준: 그래프 이론] 숨바꼭질(1697번)(정답률: 25.889%)
[문제]
수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 100,000)에 있고, 동생은 점 K(0 ≤ K ≤ 100,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일 때 걷는다면 1초 후에 X-1 또는 X+1로 이동하게 된다. 순간이동을 하는 경우에는 1초 후에 2*X의 위치로 이동하게 된다.
수빈이와 동생의 위치가 주어졌을 때, 수빈이가 동생을 찾을 수 있는 가장 빠른 시간이 몇 초 후인지 구하는 프로그램을 작성하시오.
[입력]
첫 번째 줄에 수빈이가 있는 위치 N과 동생이 있는 위치 K가 주어진다. N과 K는 정수이다.
[출력]
수빈이가 동생을 찾는 가장 빠른 시간을 출력한다.
[코드]
from collections import deque
N,K = map(int, input().split())
d = [0]*100001
def condition(N,d):
return 0 <= N <= 100000 and not d[N]
def go(N,K):
q = deque([(N,0)])
d[N]=1
while q:
N,depth = q.popleft()
if N==K:
return depth
if condition(N-1,d):
d[N-1] = 1
q.append((N-1, depth+1))
if condition(N+1, d):
d[N+1]=1
q.append((N+1, depth+1))
if condition(2*N, d):
d[2*N] = 1
q.append((2*N, depth+1))
return -1
print(go(N,K))5. [백준: 다이나믹 프로그래밍] 파도반 수열(9461번)(정답률: 43.507%)
[문제]
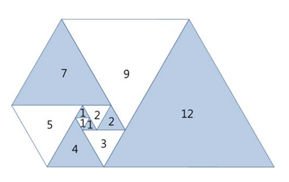
오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의 길이를 k라 했을 때, 그 변에 길이가 k인 정삼각형을 추가한다.
파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이이다. P(1)부터 P(10)까지 첫 10개 숫자는 1, 1, 1, 2, 2, 3, 4, 5, 7, 9이다.
N이 주어졌을 때, P(N)을 구하는 프로그램을 작성하시오.
[입력]
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. (1 ≤ N ≤ 100)
[출력]
각 테스트 케이스마다 P(N)을 출력한다.
[코드]
※ 코드풀이
- 점화식: $a_n = a_{n-3} + a_{n-2}$
T = int(input())
case = []
for _ in range(T):
case.append(int(input()))
d = [0]*101
d[0]=d[1]=d[2]=1
max_case = max(case)
for i in range(3,max_case):
d[i] = d[i-3] + d[i-2]
for j in case:
print(d[j-1])6. [백준: 그래프 이론] 연결 요소의 개수(11724번)(정답률: 42.014%)
[문제]
방향 없는 그래프가 주어졌을 때, 연결 요소 (Connected Component)의 개수를 구하는 프로그램을 작성하시오.
[입력]
첫째 줄에 정점의 개수 N과 간선의 개수 M이 주어진다. (1 ≤ N ≤ 1,000, 0 ≤ M ≤ N×(N-1)/2) 둘째 줄부터 M개의 줄에 간선의 양 끝점 u와 v가 주어진다. (1 ≤ u, v ≤ N, u ≠ v) 같은 간선은 한 번만 주어진다.
[출력]
첫째 줄에 연결 요소의 개수를 출력한다.
[코드]
※ 코드 풀이: 방향성이 없는 그래프에 대해서 DFS 알고리즘을 구현하는 문제이다.
import sys
sys.setrecursionlimit(10000)
input = sys.stdin.read
def connect(s,visited):
stack = [s]
while stack:
u = stack.pop()
for v in adj[u]:
if not visited[v]:
visited[v] = True
stack.append(v)
data = input().split()
N = int(data[0])
M = int(data[1])
edges = data[2:]
adj = [[] for _ in range(N)]
for i in range(M):
u = int(edges[2*i])-1
v = int(edges[2*i+1])-1
adj[u].append(v)
adj[v].append(u)
visited = [False]*N
count = 0
for i in range(N):
if not visited[i]:
connect(i, visited)
count += 1
print(count)
7. [백준: 다이나믹 프로그래밍] 2xn 타일링 2(11727번)(정답률: 58.657%)
[문제]
2×n 직사각형을 1×2, 2×1과 2×2 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.
아래 그림은 2×17 직사각형을 채운 한가지 예이다.

[입력]
첫째 줄에 n이 주어진다. (1 ≤ n ≤ 1,000)
[출력]
첫째 줄에 2×n 크기의 직사각형을 채우는 방법의 수를 10,007로 나눈 나머지를 출력한다.
[코드]
n = int(input())
d = [0]*1001
d[1] = 1
d[2] = 3
if n >= 3:
for i in range(3,n+1):
d[i] = d[i-1] + 2*d[i-2]
print(d[n]%10007)
'Coding Study' 카테고리의 다른 글
| [##프로그래머스 & 백준 coding study ## : 2024.07] (0) | 2024.07.08 |
|---|---|
| 최단 경로 알고리즘 (1) | 2024.06.06 |
| [## 프로그래머스 & 백준 coding study ##: 2024.05] (1) | 2024.05.31 |
| Depth First Search(DFS) & Breath First Search(BFS) (0) | 2024.05.14 |
| [## 프로그래머스 coding study ##: 2024.04] (0) | 2024.04.01 |



