본 글은 [논문] ExpansionNet-v2를 바탕으로 작성하였음을 명시합니다.
▶️ Image Captioning
Image captioning은 입력 데이터 Image $X_0$에 대하여 인간의 개입 없이 Image $X_0$을 묘사하는 sentence 혹은 text를 출력하는 모델을 의미합니다. 또한, Image를 이해하는 기술 ( → visual understanding )과 text를 이해하는 기술 ( → language understanding )이 필요한 multimodal task입니다.
이전 연구들에는 Image Captioning 모델로 Encoder-Decoder 기반 모델을 사용했습니다.
- Encoder : Image $X_0$로부터 visual feature를 추출합니다.
- Decoder : Image $X_0$를 가장 잘 묘사하는 sentence 혹은 text를 출력합니다.
본 글에서는 Expansion mechanism을 적용한 ExpansionNet-v2에 대해 다루고자 합니다.
▶️ Expansion mechansim
기존의 모델들은 input sequence(입력 시퀀스)의 길이에 제약을 받고, 이로 인해 더 복잡하고 다양한 이미지를 설명하는 데 어려움이 존재합니다. 이에 반해 Expansion mechansim은 input seqence의 길이에 제한을 받지 않습니다.
- Expansion mechansim은 input sequence의 내용을 더 많은 요소 또는 임의의 개수의 요소로 분배하고 처리한 후( → forward expansion ), 이 과정을 되돌리는 backward expansion을 수행함으로써 기존의 길이로 다시 복원합니다.
Expansion mechanism에 대한 구체적인 내용은 Section 1에서 다루고자 합니다.
▶️ ExpansionNet-v2
ExpansionNet-v2는 Swin-Transformer를 기반으로 하는 Encoder-Decoder 구조로 이루어져 있습니다.
또한, ExpansionNet-v2는 Encoder, Decoder에 Expansion mechanism을 사용함으로써 input seqeunce의 길이에 제약을 받지 않는다는 특성을 보유하고 있습니다.
ExpansionNet-v2에 대한 구체적인 내용은 Section 2, Section 3에서 다루고자 합니다.
▶️ Contents
1️⃣ Expansion mechanism의 구성 요소인 Static Expansion과 Dynamic Expansion에 대해서 수식과 함께 살펴 보겠습니다.
2️⃣ ExpansionNet-v2의 모델 구성(architecture)에 대해 살펴 보겠습니다.
1. Expansion Mechanism
Expansion mechanism은 크게 두 단계로 구성됩니다.
1️⃣Forward expansion
2️⃣Backward expansion
1.1 Forward Expansion
Forward expansion은 임의의 요소를 갖는 expanded sequence를 생성합니다. Expanded sequence $F^{fw}_i, \, \, i \in \{1, 2\}$를 계산하는 과정을 수식과 함께 살펴보겠습니다.
▶️ Notations
- $x$: input data
- $Q_E$: Expansion Query
- $B_E$: Expansion Bias
- $N_E$: expansion sequence의 크기
1️⃣ Length Transformation Matrix $M \in \mathbb{R}^{N_E \times N_E}$를 정의합니다.
$$M = \dfrac{Q_EK^T}{\sqrt{d_m}} \tag{1}$$
- $Q_E \in \mathbb{R}^{N_E}$ = Expansion query
- $K \in \mathbb{R}^{N_E}$ = Linear projections of input ( → $ K = w^Tx + b$)
Length Transformation Matrix $M$은 $K$와 expansion query $Q_E$간의 dot-product similarity로 정의가 됩니다. $Q_E$에 대한 자세한 식은 Section 1.3에서 살펴보겠습니다.
2️⃣ $R^{fw}_i \in \mathbb{R}^{N_E \times N_E}$을 계산합니다.
$$ R^{fw}_i = \Psi (ReLU ((-1)^i M), \epsilon), \, i \in \{ 1,2 \} \tag{2} $$
$$ \Psi(X, \epsilon)_{ij} = \dfrac{x_{ij}}{\sum^{N_2}_{z=1} x_{iz} + \epsilon} \tag{3} $$
- $ \epsilon \in \mathbb{R}^+ / \{ 0\} $: row-wise normalization function
식 (2)를 확인하면, $M$의 부호만 다르게 함으로써 2번 반복합니다. 이는 행렬이 오직 $0$으로만 구성될 가능성을 줄이기 위해서 사용합니다.
3️⃣ Expanded Sequences $F^{fw}_i \in \mathbb{R}^{N_E}$
$$ F^{fw}_i = R^{fw}_i V_i + B_E \, \, \, i \in \{ 1,2 \} \tag{4} $$
- $V_i \in \mathbb{R}^{N_E} \, \, i \in \{1,2\}$ = Linear projections of input
- $B_E \in \mathbb{R}^{N_E}$ = Expansion Bias
1️⃣ ~ 3️⃣ 과정을 통해 입력 시퀀스를 크기가 $N_E$인 Expanded Sequences로 변환할 수 있습니다.
1.2 Backward Expansion
Backward Expansion은 크기가 $N_E$인 expanded seqence $F^{fw}_i$를 기존 input sequence의 길이로 복원하는 과정입니다.
1️⃣Length Transformation Matrix $M$를 transpose합니다.
$$M^T = (\dfrac{Q_EK^T}{\sqrt{d_m}})^T$$
2️⃣ Equation (2)와 같이 $M^T$를 이용하여 $R^{bw}_i \in \mathbb{R}^{N_E \times N_E}$를 계산합니다.
$$ R^{bw}_i = \Psi (ReLU ((-1)^i M^T), \epsilon), \, i \in \{ 1,2 \} \tag{5}$$
3️⃣ 행렬 $R^{bw}_i$와 Expanded sequence $F^{fw}_i$를 곱합니다.
$$B^{bw}_i = R^{bw}_i F^{fw}_i, \, \, \, i \in \{ 1,2 \} \tag{6}$$
- $B^{bw}_i \in \mathbb{R}^{N_E}$
4️⃣Sigmoid function을 사용해 $B^{bw}_1$과 $B^{bw}_2$를 합 해 줍니다.
$$out = \sigma(S) \odot B^{bw}_1 + (1-\sigma(S)) \odot B^{bw}_2 \tag{7}$$
- $S \in \mathbb{R}^L$ : a linear projection of the input (Selector)
- $L$ = input seqeunce의 길이
식 (7)을 통해 최종적으로 expanded sequence $F^{fw}_i \in \mathbb{R}^{N_E}$는 크기가 input sequence의 원래 길이 $L$인 sequence로 복원됩니다.
앞서 살펴본 Forward Expasion과 Backward Expansion 작동 과정을 바탕으로, ExpansionNet-v2는 두 가지 방법론 Static Expansion과 Dynamic Expansion을 정의합니다.
1.3 Static and Dynamic Expansion
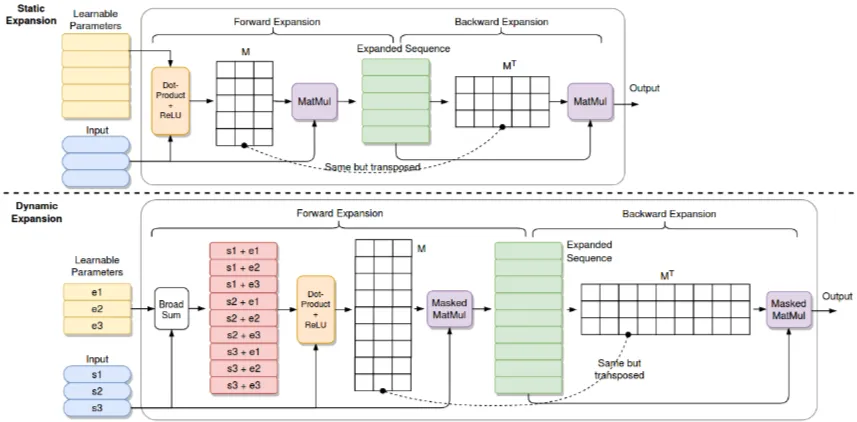
▶️Learnable Parameter
모델 학습 파라미터는 $E_Q, E_B \in \mathbb{R}^{N_E \times d_m}$으로 정의하겠습니다.
▶️ Static Expansion
Static Expansion는 forward expansion에서 사용되는 query expansion $Q_E$과 Bias expansion $B_E$에 대해서는 식 $(8)$과 같이 정의합니다.
$$Q_E = E_Q, \, \, B_E = E_B \tag{8}$$
즉, 식 (1) Length Transformation Matrix를 $M=\dfrac{Q_EK^T}{\sqrt{d_m}}=\dfrac{E_QK^T}{\sqrt{d_m}}$으로 계산하는 것입니다.
또한, Static Expansion는 input seqence $L$ 길이에 상관없이 expanded sequence의 길이는 $N_E$로 지정합니다.
[Figure 1]의 Static Expansion은 forward expansion 과정을 통해 $N_E=5$인 expanded seqence를 생성해 낸 것을 볼 수 있습니다.
▶️ Dynamic Expansion
Dynamic Expansion은 Static Expansion과는 다르게 expanded seqnece의 길이를 $N_E \cdot L$로 지정합니다. 또한, $Q_E$와 $B_E$는 식 $(9)$와 같이 정의합니다.
$$Q_E = (C^T \mathbb{H}_E)^T + (E^T_Q\mathbb{I}_E)^T, \, B_E = (C^T \mathbb{H}_E)^T + (E^T_B\mathbb{I}_E)^T \tag{9}$$
- $C \in \mathbb{R}^{L \times d_m}$ : a linear projecion of the input
- $\mathbb{H}_E \in \mathbb{R}^{L \times (L \cdot N_E)}$
$$\mathbb{H}_E = \begin{bmatrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 1 \\\end{bmatrix},\quad 1, 0 \in \mathbb{R}^{1 \times N_E}$$
- $\mathbb{I}_E \in \mathbb{R}^{N_E \times (L \cdot N_E)}$ : the column-wise concatenation of $L$ identity matrices of size $N_E \times N_E$
$$\mathbb{I}_E =[\mathbf{I}_L \, \, \, \mathbf{I}_L \, \, \cdots, \mathbf{I}_L], \, \, \mathbf{I}_L \in \mathbb{R}^{N_E \times N_E}$$
식 (9)에서 $Q_E$와 $Q_B$는 learable parameter $E_Q, E_B$와 input sequence $s_1, s_2, s_3$의 broadsum operation을 이용하여 계산됩니다.
[Figure 1]에서 Dynamic sequence는 $L=3$, $N_E=3$으로 $L \cdot N_E = 9$를 갖는 expanded sequence를 생성해 내는 것을 볼 수 있습니다.
또한, Static Expansion에서 식 (4), 식 (7)에서와 같이 행렬 곱을 하는 것 대신에 Dynamic expansion에서는 maksed 행렬 곱을 하는 것을 알 수 있습니다. 이는 특정 위치의 값을 무시하기 위해 사용되는 기법으로 Dynamic expansion에서는 미래정보를 마스킹하는 것입니다.
2. ExpansionNet-v2
ExpnansionNet-v2의 모델 구조는 [Figure 2]와 같습니다.
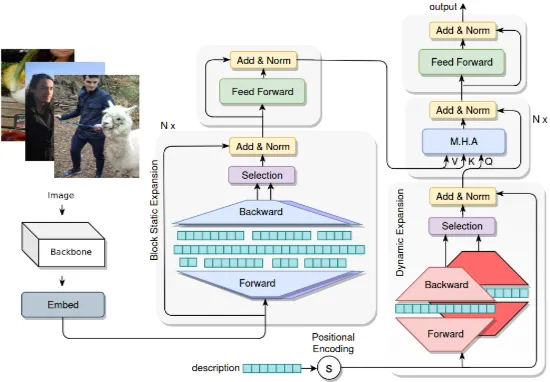
ExpansionNet-v2는 Swin-Transformer를 기반으로 Encoder-Decoder architecture를 따릅니다. Swin Transformer은 [Swin Transformer: Hierarchical Vision Transformer using Shifted Windows]을 참고하시기를 바랍니다.
1️⃣Swin-Transformer
- Input: image $A$
$$X_0 = \text{Swin-Transf}(A)$$
- Output: visual feature의 초기값 집합 ( → $X_0 = \{ x^0_1, x^0_2, \cdots, x^0_N\}, \, \, x^0_i \in \mathbb{R}^{d_m}$)
2️⃣ Encoder $N_{enc}$: Static Expansion → FeedForward blocks
Swin-Transformer의 output 값은 Encoder Layer $N_{enc}$의 입력값으로 사용됩니다. Encoder Layer의 모델 구조는 Static Expansion과 Feedfowrad blocks으로 구성됩니다. 또한, 성능 향상을 위해 skip connection과 pre-layer normalization도 이용합니다.
- Input: output of Swin-Transformer $X$
$$ E_n = X_{n-1} + StaticExp_n(Norm_n^{SE}(X_{n-1})) $$
$$ X_n = E_n + FF_n(Norm^{FF}_n(E_n)) $$
- Output: $X_{Nec}$
3️⃣Decoder $N_{dec}$: Dynamic Expansion → Cross-Attention → Feedforward blocks
Decoder layer의 입력값은 각 image에 대해 묘사하는 문장들 (ground truth) 값입니다. Decoder layer의 구조는 Dynamic expansion과 Cross-Attention, FeedForward blocks로 구성됩니다. 마찬가지로, 성능 향상을 위해 skip connection과 normalization도 이용했습니다.
- Input: $Y_0 = \{ y^0_1, y^0_2, \cdots, y^0_M\}, \, y^0_i \in \mathbb{R}^{d_m}$
$$B_n = Y_{n-1} +DynamicExp_n(Norm_n^{DE}(Y_{n-1}))$$
$$W_n = B_n + Attention(Norm^{CA}_n(B_n), X_{N_{enc}})$$
$$Y_n = W_n + FF_n(Norm^{FF}_n(W_n))$$
- Output: $Y_{dec}$
2.1 Training
ExpanionNet-v2는 모델 훈련을 크게 2단계로 이루어집니다.
먼저, Cross-entropy loss를 사용하여 모델을 사전 훈련한 후, 사전 훈련된 모델을 바탕으로 CIDEr-D 점수를 최적화하고자 강화학습을 합니다.
1️⃣ Pre-trained model → Cross Entropy loss
모델은 Cross-Entropy loss $L_{XE}$를 사용하여 사전 훈련합니다.
$$L_{XE}(\theta) = - \sum^T_{t} log(p_{\theta} (y^*_t|y^*_{1:t-1}, I))$$
$p_{\theta}(y^*_t|y^*_{1:{t-1}},I)$는 특정 시점 $t$에서 이미지 $I$와 이전 단어 $y^*_{t-1}$가 주어졌을 떄 모델이 정답 단어 $y^*_t$에 할당하는 확률을 의미합니다.
2️⃣ Optimization → CIDEr-D score
CIDEr 점수는 SCST(Self-Critical Sequence Training)를 사용하여 최적화되며, 이는 negative expected reward $L_R(\theta) = - \mathbb{E}_{y_{1:T}, \, \, p_{\theta}} [r(y_{1:T})] $를 최소화하는 방식으로 진행됩니다.
$$\nabla _{\theta} L_R(\theta) \approx -(r(y^s_{1:T}) -b)\nabla_{\theta}log p_{\theta}(y^s_{1:T})$$
- CIDEr-D는 image captioning에서 생성된 문장이 정답 문장과 얼마나 유사한 지 평가하는 지표입니다.
- SCST(Self-Critical Sequence Training)는 강화학습을 활용하여 시퀀스 생성 모델을 직접 평가 지표(CIDEr-D)에 맞게 최적화는 기법입니다.
3. Result
ExpansionNet-v2는 기존 image captioning 모델들은 Attention mechanism을 통해 seqeunce modeling을 개선했지만, 이 논문에서는 Expansion mechanism이라는 새로운 방법을 통해 sequence length의 제약을 극복하고 성능을 향상시켰다는 점에서 의의가 있습니다.
Expansion mechanism은 크게 Forward expansion과 Backward expansion으로 구성되어 있으며, ExpansionNet-v2는 expansion mechanism을 활용하여 Static expansion과 Dynamic expansion을 정의했습니다. Static Expansion은 Encoder layer에 활용되고 Dynamic Expansion은 Decoder layer에 활용됩니다.
ExpansionNet-v2의 훈련 전략은 모델의 성능을 유지하면서도 훈련 비용을 절감하는 데 기여하며, 특히 계산 자원이 제한된 환경에서 Image captioning 연구를 진행하는 데 유용합니다.
'Generative Model' 카테고리의 다른 글
| CIDEr Score (0) | 2025.03.17 |
|---|