One-Class SVM

1. One-Class Classification

One Class Classification(OCC)란, 정상 데이터와 이상 데이터 사이에 불균형이 존재할 때 정상 데이터를 정의하는 경계면을 정의하여 이상 데이터를 탐지하는 기법이다. One-Class SVM은 OCC에 사용되는 모델 중 하나로 데이터에서 이상치를 탐지하는 것을 기반으로 생성된 모델이며 kernel based soft-margin svm을 기반으로 만들어졌다. 기존의 kernel based soft-margin svm과의 차이점은 다음과 같다.

SVM	One-Class SVM
지도 학습	비지도 학습
두 클래스를 가장 잘 분류하는 초평면을 찾기 위해 여백을 최대화하는 것을 목적으로 함.	데이터를 N차원의 좌표계에 매핑한 후, 데이터와 원점을 최대한 분리하는 초평면을 찾는 것을 목적으로 함.
학습 시 모든 데이터 사용	정상 데이터만을 가지고 학습

[Figure 1] OC-SVM

2. Algorithm

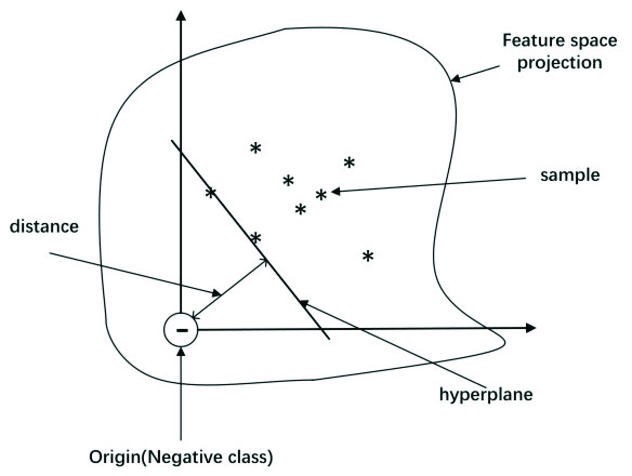
One-Class SVM의 알고리즘은 feature space(Hilbert space) 상에서 원점으로부터 대다수의 데이터(정상 데이터)를 분리하는 초평면(decision boundary, hyerplane)을 찾는 것이며 초평면의 반대편에 존재하는 극소수의 데이터가 이상치이다. 먼저, 저차원상의 데이터를 커널 함수($\phi(x)$)를 통해 고차원 상인 feature space상에 매핑한다(→ $\phi(x_i) : \mathbb{R}^p \to \mathbb{R}^q$).

• Feature space 상에서의 hyper-plane: $w^T \phi(x_i) -\rho = 0$
  • Parameter : $w \in \mathbb{R}^n, \, \rho \in \mathbb{R}$

매개변수(parameter) $w$와 $\rho$는 Quadratic Programming(QP)을 통해 찾을 수 있다. 먼저 목적함수(objective function)에 대해 살펴보겠다.

 

[Objective Function(Primal Problem)]

One-Class SVM의 목적함수는 다음과 같다.

$$\min_{w,\rho} \dfrac{1}{2}||w||^2 - \rho + \dfrac{1}{vn}\sum^n_{i=1}\xi_i \tag{1}$$

$$s.t. \, w^t\phi(x_i) \geq \rho - \xi_i, \, \xi_i \geq 0$$

 

<< 해석 (1) >>

[1]. First term: $\dfrac{1}{2}||w||^2 - \rho$

첫번째 식인 $\dfrac{1}{2}||w||^2 - \rho$은 원점으로부터 대다수의 데이터를 가장 잘 분류하는 초평면을 찾는 식이다.

 

원점과 초평면 사이의 거리를 구하면 $d(x) = \dfrac{|g(x)|}{||w||}$이다. 따라서, 원점에서 초평면 사이의 거리는 $\dfrac{\rho}{||w||}$임을 알 수 있다. 우리는 원점으로부터 대다수의 데이터를 최대한 가장 잘 분리하는 초평면을 찾는 것이 목적이었다. 이를 수식으로 표현하면, $\max_{w} \dfrac{\rho}{||w||}$이며 $\min_{w,\rho} \dfrac{1}{2}||w||^2 - \rho$로 최소화로 표현 가능하다.

 

[2]. Second Term(→ Penalty term): $\dfrac{1}{vn}\sum^n_{i=1}\xi_i$

 

$$ \xi_i = \max(0, \rho - w^t \phi(x_i))  \geq 0$$

 

OC-SVM의 경우, soft boundary로 마진(margin)에 데이터가 존재하는 것을 허용한다. 다만,오분류(→ $w^t \phi(x_i) - \rho < 0$ 영역에 존재하는 객체)된 데이터에 대해서는 $\xi_i$만큼의 패널티를 부여한다. 

• $i$번째 객체가 $w^t \cdot \phi(x_i) - \rho \geq 0$ 영역에 존재하는 경우, 즉 $i$번째 객체가 원점으로부터의 거리가 $\dfrac{\rho}{||w||}$보다 크거나 같은 경우, $\xi_i=0$으로 패널티를 부여하지 않는다.
• $i$번째 객체가 $w^t \cdot \phi(x_i) - \rho \ <  0$ 영역에 존재하는 경우, 즉 $i$번째 객체가 원점으로부터의 거리가 $\dfrac{\rho}{||w||}$보다 작은 경우, $\xi_i>0$으로 패널티를 부여한다.

$n$은 데이터의 총 개수, $\nu$는 하이퍼-파라미터이다.

 

<< 해석 (2) >>

[1]. First term (→ Regularization term) : $\dfrac{1}{2}||w||^2$

$w$가 훈련 데이터에 과적합(over-fitting)되는 것을 방지하고 일반화 성능을 향상시키는 역할을 하는 정규화 식입니다.

 

[2]. Second term: $\rho$

$\rho$는 원점과 초평면 $w$와의 거리입니다.

 

[3]. Third term (→ Regularization term) : $\dfrac{1}{vn}\sum^n_{i=1}\xi_i$

<< 해석 (1) >> 에서의 regularization term 해석과 동일합니다.

 

Primal Problem에 제약조건식이 존재하므로 Lagrangian Method를 사용해 하나의 식으로 표현하면 식 $(1)$과 같다.

$$L_p(w, \rho, \xi_i) = \dfrac{1}{2} ||w||^2 - \rho + \dfrac{1}{\nu n} \sum^n_{i=1} \xi_i - \sum^n_{i=1} \alpha_i (w^T \phi(x_i) - \rho + \xi_i) - \sum^n_{i=1} \eta_i \xi_i \tag{1}$$

[Lagrange Dual Function]

$$g(\alpha) = \min_{w, \rho} L_p(w, \rho, \xi_i)$$

 

[KKT condition]

(Stationary)

$$\dfrac{\partial L_p}{\partial w} = w - \sum^n_{i=1} \alpha_i \phi(x_i) = 0 \to w = \sum^n_{i=1} \alpha_i \phi(x_i) = 1 \tag{K1}$$

$$\dfrac{\partial L_p}{\partial \rho} = -1 + \sum^n_{i=1} \alpha_i = 0 \to \sum^n_{i=1} \alpha_i = 1\tag{K2}$$

$$\dfrac{\partial L_p}{\partial \xi_i} = \dfrac{1}{\nu n} - \alpha_i - \eta_i = 0 \to \alpha_i + \eta_i = \dfrac{1}{\nu n} \tag{K3}$$

 

(Complemetary Slackness)

$$\alpha_i(w^T \phi(x_i) - \rho + \xi_i) = 0 \tag{K4}$$

$$\eta_i \xi_i = 0 \tag{K5}$$

 

 

[Lagrange Dual Problem]

$$\max_{\alpha} g(\alpha) = \max_{\alpha}\min_{w, \rho} -\dfrac{1}{2} \sum^n_{i=1} \sum^n_{j=1} \alpha_i \alpha_j \phi(x_i)^T \phi(x_j) = -\dfrac{1}{2} \sum^n_{i=1} \sum^n_{j=1} \alpha_i \alpha_j K(x_i, x_j) \tag{3}$$

• Kernel trick: $K(x_i, x_j) = \phi(x_i)^T \phi(x_j)$

식 $(3)$에 음수를 취함으로써 최소화 문제로 변환시켰다.

$$\begin{align} \text{Find  } \alpha \;\;\text{ s.t   Minimize }\;\; \frac{1}{2}\alpha^tQ\alpha \\ \text{Subject to } e^t \alpha=1 \\ \;\; 0\leq \alpha_i \leq \dfrac{1}{\nu n}, \;\forall i \end{align} \tag{4}$$

• $e^t = (1,1,1,\cdots,1)^T \in \mathbb{R}^n$
• $Q \in \mathbb{R}^{n \times n}$
  • $Q_{ij} = \phi(x_i)^T \phi(x_j)  $

식 $(4)$를 최소화하는 $\alpha^*$과 KKT 조건을 이용하여 최적해 $w^*$와 $\rho^*$를 찾을 수 있다.

 

3. Support Vector에 대한 정의

$(K2)$, $(K3)$, $(K4)$, $(K5)$ 조건을 이용하여 support vector에 대한 정의를 하고자 한다.

• Case 1: $\alpha_i = 0$인 경우, $\eta_i =\dfrac{1}{vn} \ne 0$이므로 $\xi_i = 0$이다. -> $i$번째 객체는 non-support vector이며 $w^t\phi(x_i) - \rho > 0$ 영역에 존재하는 객체(정분류된 객체)이다.
• Case 2 : $\alpha_i = \dfrac{1}{vn}$인 경우, $\eta_i = 0$이므로 $\xi_i > 0$이다. -> $i$번째 객체는 support vector이며 $w^t\phi(x_i) - \rho < 0$영역에 존재하는 객체(오분류된 객체)이다.
• Case 3 : $ 0 < \alpha_i < \dfrac{1}{vn}$인 경우, $\beta_i > 0$이므로 $\xi_i = 0$이다. -> $i$번째 객체는 support vector이며 $\alpha_i(w^t\phi(x_i) - \rho + \xi_i) = 0$, 즉, i번째 객체는 분류경계면 위에 존재하는 객체이다.
• 즉, support vector란 $\alpha \ne 0$인 경우, $w^t\phi(x_i) - \rho \leq 0$인 영역에 존재하는 객체이다.
  • 최적해 $w$와 $\rho$를 구하는데 영향을 끼치는 객체는 support vector임을 알 수 있다.

4. Hyper-Parameter $v$의 역할

앞서 구한 두가지 조건식 $\sum^n_{i=1}\alpha_i = \sum_{i \in SV}\alpha_i = 1, \, 0 \leq \alpha_i \leq \dfrac{1}{vn}$에 대해 염두해 두고 보아야 한다.

 

[1]. 서포트 벡터 비율의 하한값

$\alpha_i$의 최대값은 $\dfrac{1}{vn}$이다. 만약, $\alpha_i$가 $\dfrac{1}{vn}$인 경우, $\sum^n_{i \in SV}\alpha_i = 1$ 조건을 만족하기 위해 필요한 support vector의 갯수는 $vn$이다. 이는 다시 말해, $vn$은 support vector 갯수에 대한 하한값이다.

 

[2]. 패널티를 부여받는 서포트 벡터 비율의 상한값

• 만약, $0 < \alpha_i < \dfrac{1}{vn}$인 경우, $\eta_i > 0$이므로 $\xi_i = 0$이다. 즉, 패널티를 부여받는 서포트 벡터의 갯수는 0개이다.
• $\alpha_i = \dfrac{1}{vn}$인 경우, $\eta_i = 0$이므로 $\xi_i \ne 0$이다. 즉, 패널티를 부여받는 서포트 벡터 개수의 최댓값은 $vn$이다.

다시 말해, $vn$는 서포트 벡터 갯수의 하한값이자 패널티를 부여받는 서포트 벡터 갯수의 상한값이다. $v$는 서포트 벡터 비율의 하한값이자 패널티를 부여받는 서포트 벡터 비율의 상한값이다. $v$값이 작을수록 서포트 벡터 갯수의 하한값이 작아지며 반대로 $v$ 값이 커질수록 서포트 벡터 갯수의 하한값이 커진다. 즉, $v$ 값이 작을수록 $w^t \cdot \phi(x_i) - \rho > 0$ 영역에 존재하는 수많은 데이터에 집중하겠다는 것을 의미한다. $v$ 값이 클수록 $w^t \cdot \phi(x_i) - \rho \leq 0$ 영역에 존재하는 데이터에 집중하겠다는 의미이다. 즉, 더 복잡한 경계면이 생성된다.

 

 

참고논문:

• One-Class SVMs for Document Classification
• Enhancing One-Class Support Vector Machines for Unsupervised Anomaly Detection