1. Support Vector Data Description(SVDD)
1.1 Definition
SVDD는 One-Class SVM과 관련된 기술이다. SVDD는 분류 경계면(hyperplane)을 찾는 것 대신에 정상데이터를 최대한 많이 포함하는 가장 작은 초구(hypersphere)를 찾는다. SVDD의 목적은 feature space 상에서 데이터를 최대한 많이 포함하는 중심은 c, 반지름은 R인 가장 작은 초구를 찾는 것이다.
| One-Class SVM | SVDD |
| 정상 데이터를 최대한 원점으로부터 멀리 위치하도록 하는 분류 경계면을 찾는 것이 목적 | 정상 데이터를 최대한 감싸안는 가장 작은 초구를 찾는 것이 목적. |
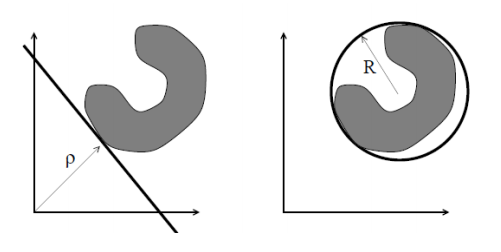
1.2 Algorithm
SVDD의 목적함수는 다음과 같다.
Objective Function(Primal problem)
$$\min_{R,c}R^2 + \dfrac{1}{vn}\sum^n_{i=1}\xi_i$$
$$s.t., \, ||\phi(x_i) - c||^2 \leq R^2 + \xi_i, \xi_i \geq 0, \forall{i}$$
[1]. First Term: $R^2$
첫번째 식인 $R^2$은 데이터를 최대한 많이 포함하는 가장 작은 초구를 찾는 식이다.
[2]. Second Term: $\dfrac{1}{vn}\sum^n_{i=1}\xi_i$
$$\xi_i = \max (0, R^2 - ||\phi(x-i)-c||^2)$$
두번째 식인 $\dfrac{1}{vn}\sum^n_{i=1}\xi_i$는 너무 많은 오분류된 데이터(초구 밖에 존재하는 데이터)를 허용하면 안 되기 때문에 오분류된 데이터에 대해 부여하는 패널티 식이다.
- $||\phi(x)-c||^2 \leq R^2$인 경우, 즉, 객체가 중심으로부터 반지름 내에 있으면 $\xi_i = 0$이다.
- $||\phi(x)-c||^2 > R^2$인 경우, 즉, 객체가 중심으로부터 반지름 밖에 있으면 $\xi_i > 0$이다.
Quadratic Programming(QP)를 통해 목적함수를 최소화하는 $c$와 $R$을 찾는다.
목적함수에 제약조건 식이 존재하므로 Lagrangian Method을 사용해 식 $(1)$에서의 $L_p$와 같이 하나의 식으로 표현해준다.
Daul Function
$$ g(\alpha_i) = \min_{R, c}L_p = R^2 + \dfrac{1}{\nu n}\xi_i - \sum^n_{i=1}\alpha_i(R^2 + \xi_i - (\phi(x_i)^t\phi(x_i) - 2c \cdot \phi(x_i) + c \cdot c)) - \sum^n_{i=1}\beta_i\xi_i, \\ \alpha_i \geq 0, \, \beta_i \geq 0 \tag{1}$$
KKT condition
(Stationary)
$$\dfrac{\partial{L_p}}{\partial{R}} = 2R(1-\sum^n_{i=1}\alpha_i)=0 \to \sum^n_{i=1}\alpha_i=1 \tag{K1 }$$
$$\dfrac{\partial{L_p}}{\partial{c}} = 2\sum^n_{i=1}\alpha_i\phi(x_i) - 2c\sum^n_{i=1}\alpha_i=0, \to c = \sum^n_{i=1}\alpha_i\phi(x_i) (\because \sum^n_{i=1} \alpha_i = 1)\tag{ K2}$$
$$\dfrac{\partial{L_p}}{\partial{\xi_i}} = \dfrac{1}{ \nu n} - \alpha_i - \beta_i = 0 \to \alpha_i - \beta_i = \dfrac{1}{\nu n}\forall{i} \tag{ K3 }$$
(Complementary Slackness)
$$ \alpha_i(R^2 + \xi_i - (\phi(x_i)^t\phi(x_i) - 2c\phi(x_i) + c^2)) = 0 \tag{ K4 }$$
$$ \beta_i\xi_i = 0 \tag{ K5 }$$
Dual Problem
KKT 조건을 이용하여 식 $(2)$와 같이 primal problem을 dual problem으로 변환시켰다.
$$\begin{align} \max_{\alpha_i} g(\alpha_i) &= \sum^n_{i=1}\alpha_i\phi(x_i)^t\phi(x_j) - \sum^n_{i=1}\sum^n_{j=1}\alpha_i\alpha_j\phi(x_i)^t\phi(x_j) \\ &= \sum^n_{i=1}\alpha_iK(x_i, x_j) - \sum^n_{i=1}\sum^n_{j=1}\alpha_i\alpha_jK(x_i, x_j) \\& \text{ s.t. } 0 \leq \alpha_i \leq \dfrac{1}{vn} \end{align} \tag{2}$$
식 $(2)$에 음수를 취해줌으로써 최소화 문제를 최대화 문제로 바꾸어주었다.
식 $(3)$을 최소화하는 $\alpha^*$를 찾음으로써 최적해 $R^*$과 $c^*$를 찾을 수 있다.
$$\begin{align} \text{Find } \alpha \;\;\text{ s.t Minimize }\;\; \frac{1}{2}\alpha^tQ\alpha-e^t Q \\ \text{Subject to } e^t \alpha=1 \\ \;\; 0\leq \alpha_i \leq \dfrac{1}{\nu n}, \;\forall i \end{align} \tag{4}$$
- $e^t = (1,1,1, \cdots, 1)^T \in \mathbb{R}^n$
- $Q \in \mathbb{R}^{n \times n}$
- $Q_{ij} = \phi(x_i)^T \phi(x_j)$
1.3 Support Vector에 대한 정의
$(K1)$ ~ $(K5)$ 조건을 이용하여 서포트 벡터에 대한 정의를 하고자 한다.
- Case 1: $\alpha_i = 0$인 경우, $\beta_i \ne 0$이므로 $\xi_i = 0$이다. 즉, $i$번째 객체는 non-support vector이며 $||\phi(x_i)-C||^2 < R^2$ 영역에 존재하는 객체이다.
- Case 2: $\alpha_i = \dfrac{1}{vn}$인 경우, $\beta_i=0$이므로 $\xi_i>0$이다. 즉, $i$번째 객체는 support vector이며 $||\phi(x_i)-C||^2 > R^2$ 영역에 존재하는 객체이다.
- Case 3: $0<\alpha_i<\dfrac{1}{vn}$인 경우, $\beta_i > 0$이므로 $\xi_i = 0$이다. 즉, $i$번째 객체는 support vector이며 $||\phi(x_i)-C||^2 = R^2$, 즉, 초구 위에 존재하는 객체이다.
즉, $\alpha_i \ne 0$인 경우 및 $||\phi(x_i)-C||^2 \geq R^2$ 영역에 존재하는 객체를 support vector라고 정의할 수 있으며 최적해 $\hat{c}$와 $\hat{R}$을 구하는데 영향을 끼치는 객체는 support vector임을 알 수 있다.
1.4 Hyper-Parameter의 성질
가우시안 커널을 사용할 경우, SVDD에 우리가 지정해줘야 하는 하이퍼 파라미터는 표준편차 $s$와 목적함수에 존재하는 $v$이다.
[표준편차 $s$]
- 가우시안 커널의 표준편차 값이 작으면 작을수록 객체에 대한 개별적인 분류 경계면이 생성된다.
- 가우시안 커널의 표준편차 값이 크면 클수록 구에 가까운 분류 경계면이 생성된다.
[$v$]
- $v$의 값이 작으면 작을수록 구 안에 존재하는 객체에 대해 집중하며 정상 데이터 영역이 커진다. 이는 구 밖에 있는 객체를 왠만하면 허용하지 않겠다는 의미를 내포하고 있으며 대부분의 데이터를 감싸안는 구가 형성된다.
- 반대로, $v$의 값이 크면 클수록 구 밖에 존재하는 객체에대해 집중하며 타이트한 구가 형성된다.
1.5 OC-SVM과 SVDD의 문제점
- 커널 행렬 때문에 계산 비용이 많이 든다.
- 커널 기반 방법론들은 근사 기법을 사용하지 않는 한 데이터 샘플에 대해 2차식으로 표현한다.
- 커널 기반 예측값들은 큰 용량의 메모리를 요구하는 서포트 벡터를 저장해야 한다.

파란색 구는 반지름 R로 정상 데이터를 모두 포함하는 가장 작은 초구이다. 만약, 새로운 데이터 $X_1$과 $X_2$가 입력된 경우, $X_1$은 기존의 정상 데이터와 매우 유사하게 분포하는 것으로 보아 정상일 가능성이 높아 보이는 반면, $X_2$는 기존의 정상 데이터 분포로부터 멀리 떨어진 것으로 비정상일 가능성이 높아 보인다. 하지만, $X_1$과 $X_2$는 우리가 최적화한 초구 안에 존재하므로 정상 데이터로 판단한다.이렇듯 SVDD는 고차원의 데이터를 변환 없이 직접 다루기 때문에 논리상 허점이 존재한다.
참고자료
'Machine Learning > Anomaly Detection' 카테고리의 다른 글
| One-Class SVM (1) | 2024.03.22 |
|---|
