본 글에서는 Gaussian Process Regression(GPR)에 대해 알기 전에 필요한 사전적인 개념에 대해 설명하고자 합니다.
목차는 다음과 같습니다.
일변량 정규분포 / 다변량 정규분포
결합 분포 / 조건부 분포
랜덤 프로세스 / 가우시안 프로세스
커널 함수(공분산 함수)
1. 일변량 정규분포 / 다변량 정규분포
[일변량 정규분포(Univariate Gaussian or Normal Distribution)]
확률 변수(random variable) $X$가 펑균이 $\mu$, 분산이 $\sigma^2$인 일변량 정규분포(Univariate Gaussian or Normal Distribution)를 따르는 경우, 확률 밀도 함수(probability denstiy distribution: pdf)는 다음과 같습니다.
$$ X \sim N(\mu, \sigma^2), \, \mu \in R, \, \sigma^2 \in R$$
$$ f_X(x;\mu,\sigma^2) = \dfrac{1}{\sqrt{ 2 \pi \sigma^2}} exp(-\dfrac{1}{2 \sigma^2}(x-\mu)^2), -\infty< x < \infty $$

[Figure 1]의 왼쪽 그림을 통해서 동일한 표준편차 $\sigma$하에서 평균 $\mu$ 값을 다르게 주었을 때는 같은 분포의 형태가 $\mu$ 값만큼 이동함을 알 수 있습니다. 반면, 동일한 평균 $\mu$하에서 서로 다른 표준편차 $\sigma$를 주었을 때는 $\sigma$값이 높아질수록 꼬리가 두텁고 $\sigma$값이 작을수록 중앙 부분이 뾰족한 형태를 갖는다는 것을 알 수 있습니다.
[다변량 정규분포(Multivariate Gaussian or Normal Distribution)]
확률 변수(random variable) $X$가 펑균이 $\mu$, 공분산이 $\Sigma$인 $n$차원의 다변량 정규분포(Multivariate Gaussian or Normal Distribution)를 따르는 경우, 확률 밀도 함수(probability denstiy distribution: pdf)는 다음과 같습니다.
$$ X \sim N_n(\mu, \Sigma) , \, \mu \in R^n, \, \Sigma \in R^{n \times n} $$
$$ f_X(x;\mu,\Sigma) = \dfrac{1}{(2 \pi)^{n/2}|\Sigma|^{1/2}} exp(-\dfrac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)), -\infty< x < \infty $$
$\Sigma$는 $Cov(x_i,x_j), {}^\forall{i,j}$의 값을 갖는 대칭 행렬(symmetric matrix)입니다.
이변량 정규분포의 경우, $x_1 \brack x_2$ $\sim N($ $\mu_1 \brack \mu_2$, $ \begin{pmatrix} \sigma_{11} & \sigma_{12} \\ \sigma_{21} & \sigma_{22} \end{pmatrix}) $, $\mu_1$과 $\mu_2$는 $x_1$, $x_2$ 각각의 independent mean(평균)입니다. 공분산 행렬(covariance matrix) $ \begin{pmatrix} \sigma_{11} & \sigma_{12} \\ \sigma_{21} & \sigma_{22} \end{pmatrix})$에서 대각 원소 $\sigma_{11}, \sigma_{22}$는 $x_1$, $x_2$ 각각의 independent variance(분산)이며 비대각 원소 $\sigma_{12}$, $\sigma_{21}$은 $x_1$과 $x_2$ 사이의 상관계수(correlation) 값입니다.
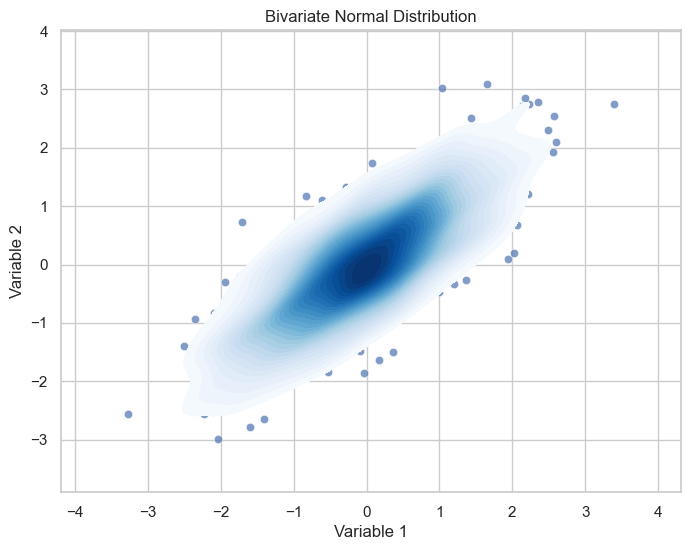
[Figure 2]는 $\mu = \begin{pmatrix} 0 \\ 0 \end{pmatrix}$, $\Sigma = \begin{pmatrix} 1 & 0.8 \\ 0.8 & 1 \end{pmatrix}$인 이변량 정규분포의 그림입니다. 즉, 다변량 정규분포는 일변량 정규분포를 둘 이상의 변수로 일반화한 것입니다.
| Parameter | Multivariate Normal Distribution | Univaraite Normal Distribution |
| $\mu$ | 평균 벡터 | 평균 스칼라 |
| $\Sigma$ | 공분산 행렬 (대각선 요소 = 각 변수의 분산, 비대각선 요소 = 변수 간 공분산) |
분산 스칼라 |
2. 조건부 정규 분포
[결합 정규분포(Joint Gaussian Distribution)]
$X \in \mathbb{R}^{m}$와 $Y \in \mathbb{R}^{n}$의 결합 정규분포(Joint Gaussian Distribution)의 기댓값과 공분산은 다음과 같습니다.
$$ \begin{bmatrix} X \\ Y \end{bmatrix} \sim N(\mu, \Sigma)$$
$$ \mu=\begin{bmatrix} \mu_X \\ \mu_Y \end{bmatrix}, \, \Sigma = \begin{bmatrix} \Sigma_{XX} & \Sigma_{XY} \\ \Sigma_{YX} & \Sigma_{YY} \end{bmatrix} \tag{1}$$
[조건부 정규분포(Conditional Gaussian Distribution)]
식 $(1)$을 이용하여 조건부 정규분포 $p(X|Y)$의 기댓값 $\mu_{X|Y}$와 공분산 $\Sigma_{X|Y}$를 구할 수 있습니다.
$$X|Y \sim N(\mu_{X|Y}, \Sigma_{X|Y})$$
$$\mu_{X|Y}= \mu_X + \Sigma_{XX}\Sigma_{YY}^{-1}(Y-\mu_Y), \, \Sigma_{X|Y} = \Sigma_{XX} - \Sigma_{XY}\Sigma^{-1}_{YY}\Sigma_{YX}$$
3. Random Process & Gaussian Process
Sectioin 3 내용은 '최성준님의 Bayesian Deep Learning ' 내용을 바탕으로 작성하였습니다.
Bayesian Deep Learning 강좌소개 : edwith
- 최성준
www.edwith.org
[랜덤 프로세스(Random Process)]
$$ X_t(w), \, t \in I$$
랜덤 프로세스란 어떤 모수(parameter)로 인덱스(index, $t$)된 확률 변수(random variable, $X_t$)의 모임이며 보통 무한개(infinite)의 확률 변수들로 구성된 시퀀스(sequence)입니다. 랜덤 프로세스에서 나올 수 있는 모든 결과들의 집합을 표본 공간(sample space, $w$)이라고 합니다.
1. random sequence, random function or random signal: $w$(함수들의 공간으로 매핑)
$$X_t : \Omega \to \text{the set of all sequences or functions}$$
2. indexed family of infinite number of random variables: $t \in (0, \infty)$
$$X_t : I \to \text{set of all random variables defined on } \Omega$$
3. $X_t: \Omega \times I \to \mathbb{R}$
4. 만약 time $t$를 고정시킨다면, random process(: sampling function)는 random variable(: sampling value)이 됩니다.

[Figure 3]를 참조하면 sample space $\Omega$에서 랜덤하게 함수 $X_t(w)$를 샘플링하는 것을 알 수 있습니다.
더 자세한 내용은 '최성준님의 Bayesian Deep Learning ' 의 강좌를 듣는 것을 추천합니다.
[가우시안 프로세스(Gaussian Process)]
만약, 랜덤 프로세스 $X_t$에서 임의의 샘플 $k$개를 뽑았을 때($X_{t_1}, \cdots, X_{t_k}$) 결합 정규 분포(Joint Gaussian Distribution)를 따른다면 랜덤 프로세스 $X_t$는 가우시안 프로세스(Gaussian process)라고 정의합니다.
$$X_t \sim GP(m(t), k(t,s)), \, t \ne s$$
- 평균 함수( mean function ): $m(t) = E[X_t]$
- 공분산 함수( covariance function ): $k(t,s) = cov(X_t, X_s)$ (서로 다른 시점 간의 관계)
- 만약 공분산 함수가 두 개의 시점의 차 $t-s$에 대한 함수인 경우는 $X_t$는 stationary하다고 정의한다.
4. 커널 함수(공분산 함수)
평균 함수는 보통 0으로 설정하며($m(x)=0$) 모델링하는 함수의 형태에 대한 사전 지식(prior knowledge)을 반영하는 부분은 커널 함수(공분산 함수, $k(t,s)$)입니다. 커널 함수는 공간적 또는 시간적 분리를 변화시키면서 두 확률변수가 얼마나 많이 변하는지를 설명합니다.
커널 함수의 경우 '대칭성(Symmetric)', '양의 정부호성(Positive Semi-definite)', '무한 차원의 특징 매핑(Infinite-Dimensional Feature Mapping)'의 조건을 만족해야 하며 커널 함수의 종류는 다음과 같습니다.
[커널 함수 $k(t,s)$ 종류]
1. 선형 커널(linear kernel): $k(t,s) = t^Ts$
2. 다항식 커널(polynomial kernel) $k(t,s) = (a t^T s + c)^d$
3. 가우시안 라디언스 커널(Gaussian RBF kernel): $k(t,s) = exp(-\dfrac{||t-s||^2}{2 \sigma^2})$
4. 시그모이드 커널(Sigmoid kernel): $k(t,s) = tanh(a t^T s + c)$
다음글에서는 본 내용을 토대로 본격적으로 Gaussian Process Regression(GPR)에 대해서 설명하고자 합니다.
참고논문: [An Intuitive Tutorial to Gaussian Process Regression]
'Gaussian Process > Gaussian Process' 카테고리의 다른 글
| [Gaussian Process (2)]: Gaussian Process Regression(GPR) (0) | 2023.12.22 |
|---|
