[Graph Gaussian Process(GGP)]: Bayesian Semi-supervised Learning with Graph Gaussian Process(GGP)

본 글은 논문 [Bayesian Semi-supervised Learning with Graph Gaussian Process(GGP)]를 바탕으로 작성하였으며 Gaussian Process(GP)를 기반으로 Graph($G$) 상에서 어떻게 적용하는지를 중점으로 다룬 내용입니다.

 

0. Background

[Graph]

Graph($G$)에 대한 정의 및 구성은 다음 글을 참고하시면 좋을거 같습니다.

Graph Structure

Graph $G$ 혹은 network는 데이터 점들(node)간의 관계(relationship)을 묘사합니다.

• $G=(V,E), \, V : \text{node,vertices }, \, E: \text{edge}$
• $X$: node feature matrix, 각 node들의 feature를 나타낸 행렬
• $ A = \begin{cases}
     1 &\text{if } (v_i,v_j) \in E \\
     0 &\text{if } (v_i,v_j) \notin E
  \end{cases} $: Adjacency matrix(인접행렬)
  • 두 node가 연결되어 있으면 $1$, 아니면 $0$

<< "Graph Laplacian" >>

Self-loop가 존재하지 않은 undirected binary graph $G = (V,E)$의 adjacecny matrix $A$가 주어진 경우, graph laplacian(그래프 라플라시안) $L$은 다음과 같습니다. 

$$L = D - A$$

• $D \in \mathbb{R}^{N \times N}$: diagonal node degree matrix

라플라시안 행렬 $L$은 symmetric하고 diagonalizable하기 때문에 eigen-decomposition이 가능합니다.

$$L = U\Lambda U^T$$

• the columns of $U \in \mathbb{R}^{N \times N}$: the eigenfunctions of $L$
• diagonal of $\Lambda \in \mathbb{R}^{N \times N}$: eigenvalues

그래프 라플라시안 행렬 $L$은 graph filter 혹은 kernel로 유용하게 사용됩니다. 논문 [Matern Gassuian Process on Graphs]에서 자세하게 다룹니다.

 

[Gaussian Process(GP)]

Gaussian Process에 대한 정의는 다음 2개의 글을 참고하시면 좋을거 같습니다.

Gaussian Process(1): Mathematical Basics

 

[Gaussian Process (2)]: Gaussian Process Regression(GPR)

<< "Prior distirbution of GP" >>

$$f \sim GP(m(x), k(x,x'))$$

GP는 함수에 대한 분포로 랜덤 프로세스 $X$에서 임의의 샘플 $k$개를 뽑았을 때($X_{1},X_{2}, \cdots, X_{k}$) 결합 정규 분포(Joint Gaussian Distribution)을 따른다면 랜덤 프로세스 $X$는 GP라고 정의합니다.

• 평균 함수(mean function): $m(x) = E[f(x)]$ (보통 $0$으로 설정합니다.)
• 공분산 함수(covariance function) $k(x,x') = cov(x,x')$(공분산 함수는 GP의 핵심이자 함수의 형태(shape)을 결정하는 부분입니다.)

<< "Posterior distirbution of GP" >>

$$f_*|x_*,X,f \sim N(\mu_*, \sigma^2_*)$$

• $\mu_* = K(x_*,X)K(X,X)^{-1}f$
• $\sigma_*=k(x_*,x_*)K(X,X)^{-1}K(X,x_*)$
• $X \in \mathbb{R}^D$: training dataset
• $x_* \in \mathbb{R}$: new data point

<< "Scalable Variational Inference for GP" >>

GP의 경우 계산 비용이 $O(N^3)$($N$: the number of training data points)으로 대규모의 데이터에 대해서는 계산 비용이 크다는 단점이 존재합니다. 이에 대한 해결방안으로 variational inference 방법을 이용합니다. $M$개의 inducing points $Z=[z_1,z_2,\cdots, z_M]^T, \, z_j \in \mathbb{R}^D$가 존재하는 경우, GP 함수 $f(x)$에서 랜덤하게 $M$개의 샘플을 뽑은 random variable(variational parameter) $u = [f(z_1),f(z_2),\cdots,f(z_M)]^T$를 통해 conditional GP를 제안합니다. 

$$f(x)|u \sim GP(K(Z,X)^TK(Z,Z)^{-1}u, K_\theta(X,X)-K(Z,X)^TK(Z,Z)^{-1}K(Z,X))$$

• $K(Z,X)=[k_\theta(z_1,X),k_\theta(z_2,X),\cdots,k_\theta(z_m,X)]$
• $[K(Z,Z)]_{ij} = k_\theta(z_i,z_j)$
• $p(u) = N(0,K(Z,Z))$: Variational prior distribution

$u$의 variational posterior $q(u)$는 평균이 $m$이고 공분산이 $S$인 다변량 정규 분포를 따릅니다.

Evidence Lower Bound(ELBO) 목적함수인 식 $(1)$을 최대화(maximize)하는 variational parameter $m,S, \{z_m\}^M_{m=1}$와 kernel hyper-parameter $\theta$를 찾습니다.

$$L(\theta, Z, m, S) = \sum^N_{n=1}E_{q(f(x_n))}[log(p(y_n|f(x_n)))] -  KL[q(u)||p(u)] \tag{1}$$

 

[Graph based Semi-supervised Learning(준지도 학습)]

준지도 학습은 label $y$가 극소수 존재하는 경우로 labeled data를 활용하여 unlabeled data의 label $y$를 예측하는 함수를 학습하는 것을 목표로 합니다. 준지도 학습은 크게 두 종류로 'Transductive Learning'과 'Inductive Learning'으로 나눌 수 있습니다.

• Transductive Learning
• Inductive Learning

만약, 데이터셋 $D = \{ \{x_i,y_i\}^l_{i=1}, \{x_j\}^u_{j=1} \}$($l$: the number of labeled samples, $u$: the number of unlabeled samples, $y_i$: the label of the labeled samples)가 존재하는 경우,  transductive learning은 labeled data만 가지고 학습하여 unlabaled data를 예측하는 함수 $f: X \to Y$를 학습합니다. 반면, Inductive learning의 경우, labeled data와 unlabeled data를 모두 활용하여 새로운 데이터에 대한 예측 함수 $f: X \to Y$를 학습합니다.

 

논문에서는 transductive learning을 기반으로 설명을 하며 graph based semi-supervised learning에 대한 Gaussian Process(GP) model을 제안합니다. 

 

---

1. Graph Gaussian Process(GGP)

▶ Notation

• $N$: the size of data(노드의 개수)
• $X=[x_1,x_2,\cdots,x_N]^T \in \mathbb{R}^{N \times D}$: node feature matrix
  • $x_i \in \mathbb{R}^D$: D-dimensional features(각 node는 $D$차원의 특성 벡터)
• $A \in \{0,1\}^{N \times N}$: symmetric binary adjacency matrix(데이터 점들(node)간의 관계를 나타내는 행렬)
  • $ A = \begin{cases}
       1 &\text{if } (v_i,v_j) \in E \\
       0 &\text{if } (v_i,v_j) \notin E
    \end{cases} $
• $Y = Y_O \cup Y_U$: label(각 node의 label)
  • $Y_O = \{y_1, y_2, \cdots, y_o\}, y_i \in \{1,2, \cdots, k\}$: observed label
  • $Y_U = \{y_o, y_{o+1}, \cdots, y_N\}$: unobserved label

▶ Algorithm

Graph Gaussian Process(GGP)는 조건부 분포(conditional distribution) $p_{\theta}(Y|X,A)$를 명시하며 예측 분포(predictive distribution) $p_{\theta}(Y_U|Y_O,X,A)$를 통해 $Y_U$를 예측합니다. 

 

※ ※ GP와는 다르게 GGP의 경우 조건부 분포를 사용합니다.

[Figure 1] Graph Gaussian Process(GGP)

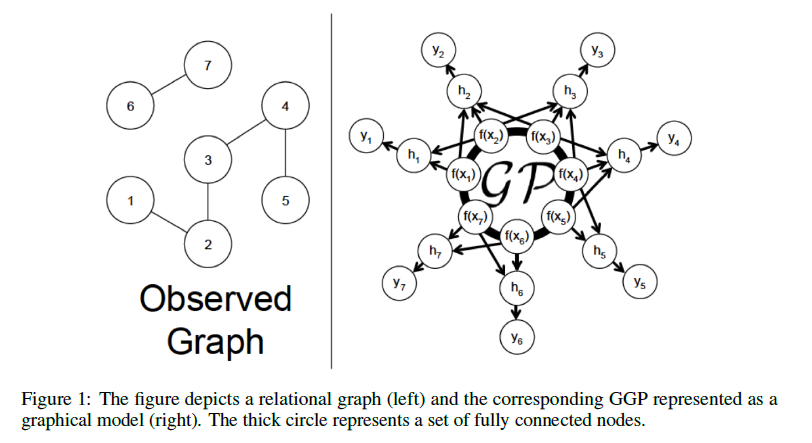
먼저, 결합 분포 식 $(2)$를 정의하겠습니다.

$$ p_{\theta}(Y,h|X,A) = p_{\theta}(h|X,A)\Pi^N_{n=1}p(y_n|h_n) \tag{2} $$

식 $(2)$는 conditionally independent likelihood $p(y_n|h_n)$의 곱과 GGP prior $p_{\theta}(h|X,A)(\theta: \text{hyper-parameter})$로 표현된 GGP posterior $p_{\theta}(Y,h|X,A)$으로 우리의 주 관심인 multi-class classification 관련 식입니다. 

 

※참고: $p(y_n|h_n)$은 robust max likelihood에 의해 주어집니다.

 

Question: 그럼 GGP prior $p_{\theta}(h|X,A)$를 어떻게 구축하는가?

GGP prior은 GP $f(x)$를 통해 건축합니다. 

 

각 node는 $D$ 차원의 feature $X$를 나타내며 node마다 Gaussian Process Latent Function $f(x): \mathbb{R}^D \to \mathbb{R}$을 줍니다.

$$f(x) \sim GP(0,k_{\theta}(x,x'))$$

[Figure 1]을 참조하면 7개의 node는 모두 GP를 따르는 것을 알 수 있습니다. 그래프 $G$의 경우, node간의 관계(relationship)를 묘사한 데이터인데 각 node의 label을 예측하는 과정에서 이웃 노드 $x_j, \, j \in N_e(n)$의 정보를 이용할 수 있습니다. 이웃 노드 $x_j, \, j \in N_e(n)$의 정보와 타겟 노드 $x_n$의 정보는 단순히 Adjacency matrix $A$에 의해 주어진 1-hop neighbourhood에 대한 $f$의 평균값으로 aggregate하고자 합니다.

 

$$h = \dfrac{f(x_n) + \sum_{l \in N_e(n)}f(x_l)}{1+D_n} \tag{3}$$

•  $N_e(n) = \{l: l \in \{1,2,\cdots,N\}, A_{nl} = 1\}$
• $D_n = |N_e(n)|$

식 $(3)$를 latent likelihood parameter vector $h \in \mathbb{R}^{N \times 1}$으로 정의하겠습니다. 우리가 정의한 $h$를 통해 GGP prior은 다변량 정규분포를 따르는 것을 확인할 수 있습니다.

$$p_{\theta}(h|X,A)=N(0, PK(X,X)P^T)$$

• $P=(I+D)^{-1}(I+A)$
• $[K(X,X)]_{ij}=k_{\theta}(x_i,x_j)$

[Proof]

식 $(3)$를 값이 아닌 vector로 표현하면 $h=(I+D)^{-1}(I \cdot f(X) + A \cdot f(X)) = (I+D)^{-1}(I+A)f(X)(D=(|N_e(1)|, \cdots,|N_e(N)|))$입니다. 

• $E[h|X,A]=(I+D)^{-1}(I+A)E[f(x)]=0$
• $Var[h|X,A]=(I+D)^{-1}(I+A)Var[h|X,A](I+A)^T((I+D)^{-1})^T = PK(X,X)P^T$

공분산 구조(covariance structure)는 다음과 같습니다.

$$Cov(h_m, h_n) \\= \dfrac{1}{(1+D_m)(1+D_n)} \sum_{i \in \{m \cup N_e(m)\}}\sum_{j \in \{n \cup N_e(n)\}}k_{\theta}(x_i,x_j) \\= <\dfrac{1}{1+D_m}\sum_{i \in \{m \cup N_e(m)\}} \phi(x_i), \dfrac{1}{1+D_n}\sum_{j \in \{n \cup N_e(n)\}} \phi(x_j) >_H \tag{4}$$

• $\phi(\cdot)$은 the base kernel $k_{\theta}(\cdot, \cdot)$에 상응하는 feature map입니다.

[Proof]

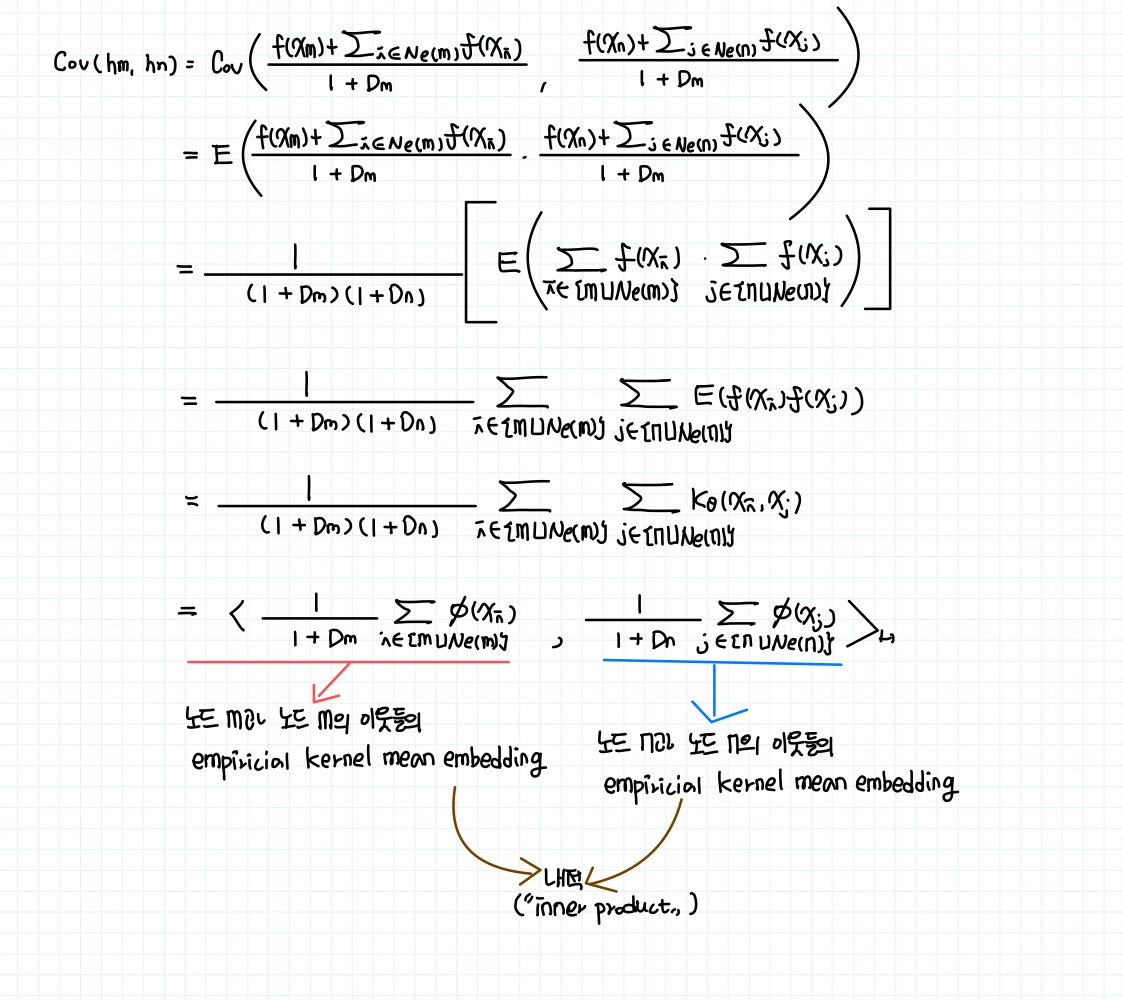
식 $(4)$sms node $m$과 node $n$의 1-hop neighborhood의 관측된 $f(\cdot)$에 상응된 empirical kernel mean embedding 사이의 내적입니다.

 

GGP는  node feature $\{(\{x_i| i \in \{n \cup N_e(n)\}\}, y_n)\}^O_{n=1}$에 대한 classification model에 대한 분포입니다. 관측되지 않은 데이터의 경우는 empirical kernel mean embedding $\hat{\mu}_n$으로 표현 가능합니다.

$$\hat{\mu}_n = \dfrac{1}{1+D_n} \sum_{j \in \{n \cup N_e(n)\}} \phi(x_j) $$

즉, prior $h$는 equivalent하게 $h \sim GP(0, <\hat{\mu}_m, \hat{\mu}_n>_H)$로도 표현 가능합니다. 

 

2. Variational Inference with Inducing Points

만약, 데이터가 대규모인 경우 계산 비용이 크기 때문에 GGP에서도 $M$개의 inducing points $\{z_m\}^M_{m=1}$을 이용해 inducing random variables $u = [f(z_1), \cdots, f(z_m)]^T$를 GP $f(x) \sim GP(0,k_\theta(x,x'))$로부터 샘플링합니다. 결과적으로 $h_n$과 $f(z_m)$ 사이의 공분산 함수는 다음과 같습니다.

$$Cov(h_n, f(z_m)) = \dfrac{1}{D_n+1} [k_{\theta}(x_n, z_m) + \sum_{l \in N_e(n)}k_{\theta}(x_l, z_m)]$$

Variational Posterior distribution $q(u) = N(m,SS^T), \, m \in \mathbb{R}^{M \times 1}, \, S \in \mathbb{R}^{M \times M}: \text{lower triangular}$입니다. 조건부 가우시안 분포를 통해 $q(u)$는 우리의 주관심 variational gaussian distribution $q(h)$를 도출할 수 있습니다. 또한, Evidence Lower Bound(ELBO) 목적함수인 식 $(1)$을 최대화(maximize)하는 variational parameter $m,S, \{z_m\}^M_{m=1}$와 kernel hyper-parameter $\theta$를 찾을 수 있습니다.

 

---

본 글은 Graph 상에 GP를 적용한 모델 Graph Gaussian Process(GGP)를 소개하였습니다. 결국에는 각 노드에 GP 분포를 걸어 latent parameter $h$로 단순히 1-hop neighborhood의 평균값으로 이웃 정보를 aggregate했다는 점과 GGP로는 조건부 분포를 사용하였다는 점이 핵심입니다.