본 글은 논문 [Multivariate Time-series Anomaly Detection via Graph Attention Network(MTAD-GAT)]을 바탕으로 multivariate time-series anomaly detection 방법론인 MTAD-GAT에 대해 설명하고자 합니다.
0. Background
▶ Time series Anomaly Detection
시계열(time series) 데이터는 시간의 흐름에 따라 순차적으로(sequentially) 기록된 데이터입니다. 일변량 시계열 데이터(univariate time series)는 변수가 1개인 시계열 데이터, 다변량 시계열 데이터(multivariate time series)는 변수가 여러 개인 시계열 데이터를 의미합니다. 즉, 일변량 시계열 데이터를 여러 개 모아두면 다변량 시계열 데이터가 됩니다.
기존의 univariate or multivariate time series anomaly detection 방법론에는 다음과 같이 존재합니다.
| Univariate Models | Multivariate Models | |
| Forecasting based model | Reconstruction based model | |
| Hypothesis Testing | LSTM-NDT | LSTM-based Encoder-Decoder |
| Wavelet Analysis | Hierarchical Temporal Memory(HTM) | Generative Adversarial Network(GAN) |
| SVD | Bayesian Network(BN) | MAD-GAN |
| ARIMA | DAGMM | GAN-Li |
| DONUT | LSTM-VAE | |
| SR-CNN (Spectral Residual(SR)+CNN) |
OmniAnomaly | |
다변량 시계열 데이터 기반 이상치 탐지 방법론은 크게 예측 기반 모델(forecasting based model)과 reconstruction based model(재건축 기반 모델)로 분류할 수 있습니다. 예측 기반 모델의 경우, 예측 오류(prediction error)를 기반으로 비정상 데이터를 탐지합니다. 재건축 기반 모델의 경우, 잠재 변수(latent variables)를 기반으로 입력 데이터를 재건축함으로써 전체 시계열 데이터의 representation vector를 학습합니다.
즉, 예측 기반 모델은 다음 시점을 예측하도록 설계되어 있고 재건축 기반 모델은 전체 시계열 데이터의 분포를 추정하도록 설계되어 있습니다. 또한, 예측 기반 모델과 재건축 기반 모델은 서로 보완적임이 증명된 요한 사실이 알려져 있습니다.
▶ 서로 다른 일변량 시계열 데이터(변수)간의 관계의 중요도
기존 시계열 데이터 기반 이상치 탐지 방법론은 변수간의 관계를 고려하지 않습니다.
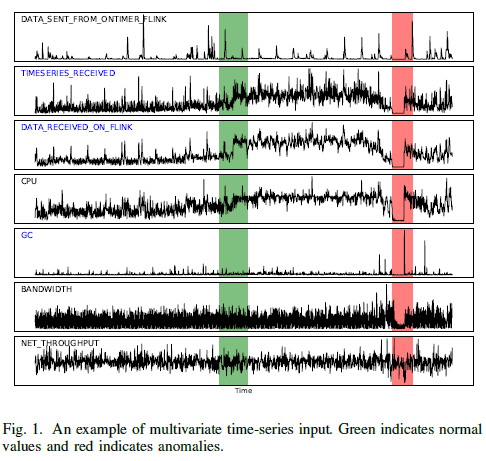
총 7개의 변수가 존재하는 다변량 시계열 데이터 자료입니다. 각 변수는 일변량 시계열 데이터이며 서로 다른 패턴을 보이고 있습니다.
- 변수 ‘DATA_RECEIVED_ON_FLINK’와 변수 ‘TIMESERIES_RECEVIED’에서 sudden change(or obvious boost)가 존재하지만 다른 변수의 변화가 없기 때문에 전체적인 시스템에서는 정상 구간으로 판단합니다.
- 반면, 변수 'GC'에서 sudden change(or obvious boost)가 존재하는 구간에서는 다른 변수도 같이 변화하였으므로 전체적인 시스템에서 비정상 구간으로 판단합니다.
이처럼 다변량 시계열 기반 이상치 탐지 방법론에서는 서로 다른 분포를 가진 시계열 데이터 사이의 상관관계(인과관계)를 고려하는 것은 중요합니다. 변수간의 관계도 같이 학습할 경우 유의미한 성능 향상도 보인다고 합니다. MTAD-GAT에서는 변수 간의 관계를 graph attention을 통해 학습합니다.
▶ Graph Attention Mechanism
[Graph란?]

Graph 란, 방향성이 있거나(directed) 없는(undirected) 엣지(edge)로 연결된 노드(node, vertices)의 집합입니다.
$$G = (V,E)$$
- $V = \{v_i\}_{i=1,\cdots,p}, \, v_i \in \mathbb{R}^n$: node의 집합
- $E=\{e_{ij}\}$: edge의 집합
[Adjacency matrix란?]
그래프 구조(graph structue)는 adjacency matrix(인접행렬) $A \in \mathbb{R}^{p \times p}$로 표현가능합니다.
$$A = \begin{cases} 1 &\text{if } (v_i,v_j) \in E \\ 0 &\text{if } (v_i,v_j) \notin E \end{cases}$$
두 노드 사이에 엣지가 존재하는 경우$((v_i,v_j) \in E)$, $1$ 아니면 $0$인 원소를 갖는 행렬입니다.
[Graph Attention Network]
$n$개의 노드를 가진 그래프가 주어졌을 때 각 노드 $\{v_1,v_2,\cdots, v_n\}$는 $m$차원의 feature vector입니다.
$$h_i = \sigma(\sum^L_{j=1} \alpha_{ij} v_j) \tag{1}$$
- $h_i$: 노드 $v_i$의 output representation
- $\sigma$: sigmoid activation function
- $L=N_i$: 노드 $v_i$의 이웃 노드
- $\alpha_{ij}$: attention score 값으로 타겟 노드 $v_i$에 대한 이웃 노드 $v_j, j \in N_i$의 기여도(중요도)
식 $(1)$을 통해 GAT layer는 각 노드의 feature vector $v_i=h_i^{(0)}, \, i \in \{1,2, \cdots, n\}$를 이웃 노드의 기여도에 따라 서로 다른 가중치 $\alpha_{ij}$를 부여함으로써 이웃 노드의 정보를 종합하여 학습시킵니다. Attention score $\alpha_{ij}$의 계산과정은 다음과 같습니다([Figure 2] 참조).

$$e_{ij} = LeakyReLU(w^T \cdot (v_i \oplus v_j)) \in R^{2m}$$
- $\oplus$: concatenate
- 유사도 함수: 1-layer feed forward network
$e_{ij}$는 타겟 노드 $v_i$와 $v_j$의 유사도를 1-layer feed forward network를 통해 계산한 값입니다. $e_{ij}$ 값을 정규화하기 위해 softmax function을 통해 최종적으로 attention score $\alpha_{ij}$ 값이 도출됩니다.
$$\alpha_{ij} = \dfrac{exp(e_{ij})}{\sum^L_{l=1}exp(e_{il})}$$
즉, GAT는 $(v_i, v_j), \, j \in N_i$의 유사도(노드 간의 관계) $\alpha_{ij}$와 이웃 노드의 정보 $v_j$를 이용하여 타겟 노드의 feature vector $v_i$를 학습합니다.
1. Methodology
먼저 MTAD-GAT의 전체 프레임워크 및 핵심에 대해 간략하게 설명하고 [section 1-2], [section 1-3]에서 자세하게 다루겠습니다.

[Step 0] 데이터 전처리 단계로 normalization 및 cleaning을 수행합니다.
[Step 1] 각 univariate time series에 대해서 kernel size가 $7$인 $1$-D convolution을 수행함으로써 local feature를 추출합니다.
[Step 2] 서로 다른 일변량 시계열 데이터(변수)간의 인과관계를 포착하는 feature-oriented GAT layer와 서로 다른 시점(timestamp)간의 관계를 학습하는 time-oriented GAT layer를 통해 '변수 간의 관계', '시점 간의 관계'를 병렬하게 학습함으로써 각 노드의 feature vector를 업데이트합니다.
[Step 3] 1-D convolution layer의 산출값, feature-oriented GAT layer의 산출값 그리고 Time-oriented GAT의 산출값을 하나로 합칩니다.
[Step 4] Gated Recurrent Unit(GRU)를 통해 시계열 데이터에 존재하는 연속적인 패턴(sequential pattern)을 학습합니다.
[Step 5] GRU의 산출값을 이용하여 Forecasting based model과 Reconstruction based model을 학습합니다. 각 시점에 대한 이상치 점수(inference score)를 두 모델의 산출값을 결합하여 계산합니다.
1.1 Data Preprocessing
▶ Problem definition
- 입력값(input)은 다변량 시계열 데이터이며 $\mathbf{x} \in \mathbb{R}^{n \times k}$로 명시하겠습니다. $n$은 시점(timestamp)의 길이 혹은 sliding window의 크기입니다. $k$는 feature의 개수로 서로 다른 일변량 시계열 데이터의 개수입니다.
- 산출값(output)은 $i^{th}$ 시점이 정상인지 비정상인지에 $0$ 또는 $1$ 값이며 $y \in \mathbb{R}^n, \, y_i \in \{0,1\}$으로 명시하겠습니다.
▶ Data Preprocessing
모델의 robust를 향상시키고자 각 일변량 시계열 데이터마다 normalization과 cleaning을 수행합니다. Normalization의 경우는 훈련 데이터 $\mathbf{x}^{(Train)}_i$와 테스트 데이터 $\mathbf{x}^{(Test)}_i$에 모두 적용되지만 cleaning은 오직 훈련 데이터 $\mathbf{x}^{(Train)}_i$에 대해서만 수행합니다.
1). Normalization
각 일변량 시계열 데이터셋의 최댓값/최솟값을 이용하여 정규화를 수행하였습니다.
$$\tilde{x}_{ij} = \dfrac{{x}_{ij}-min(\mathbf{x}^{(Train)}_i)}{max(\mathbf{x}_{i}^{(Train)})-min(\mathbf{x}_{i}^{(Train)})} \\ i \in \{1,2, \cdots, k\}, \, j \in \{1,2, \cdots, n\}$$
- $min(\mathbf{x}_{i}^{train})$: 일변량 시계열 데이터셋의 최솟값
- $max(\mathbf{x}_{i}^{train})$: 일변량 시계열 데이터셋의 최댓값
2) Data Cleaning
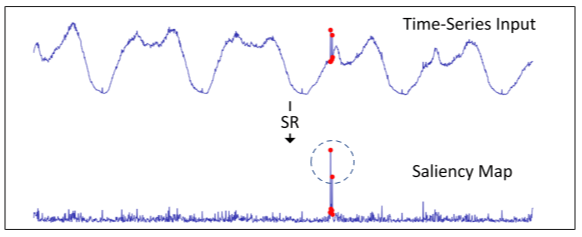
다변량 시계열 데이터 이상치 탐지 방법론 forecasing-based model과 reconstruction based model은 학습 시 훈련 데이터에 존재하는 비정상 데이터에 매우 민감합니다. 일변량 시계열 데이터 이상치 탐지에 우수한 성능을 보이는 Spectral Residual(SR)을 통해 각 일변량 시계열 데이터에 존재하는 비정상 데이터를 탐지하고 이를 정상 데이터로 대체하고자 합니다. Spectral Residual(SR)에 대한 자세한 내용은 [SR-CNN(1)]과 [SR-CNN(2)]를 참조하시기 바랍니다.
$O(\tilde{x}_{ij}) = \begin{cases} 1 &\text{if } \dfrac{S(\tilde{x}_{ij})-\bar{S(\tilde{x}_{ij})}}{\bar{S(\tilde{x}_{ij})}} > \tau \\ 0 &\text{otherwise}\end{cases}$
시점 $j^{th}$에 대하여 SR의 산출값이 특정 임계값 $\tau$보다 큰 경우, 이상치로 판단하고 주변 시점의 정상 데이터로 대체하며 훈련 데이터셋 $\mathbf{x}^{(Train)}_i$에 대해서만 적용합니다.
3) 1-D convolution Layer
Convolution neural network를 통해 전처리된 데이터 $\tilde{x} \in \mathbb{R}^{n \times k}$를 바탕으로 각 일변량 데이터의 지역적인 정보를 추출합니다. 즉, 각 시점별 feature vector를 1-D convolution layer을 통해 학습하여 지역적인 정보를 추출합니다. 1-D convolution layer의 산출값 $\tilde{x}$의 차원은 $n \times k$라고 가정하겠습니다.
- 1-D convolution layer의 자세한 내용은 아래 링크를 참조하시면 좋을것 같습니다.
[PyTorch] 시계열 데이터를 위한 1D convolution과 1x1 convolution
오늘은 시계열 데이터처리에 많이 사용되는 1D convolution이 PyTorch에 어떻게 구현되어 있는지와 어떤 파라미터가 존재하는지 차원은 어떻게 계산하는 지를 정리해 보려고 한다. 자꾸 까먹는 나 자
sanghyu.tistory.com
1.2 Graph Attention Layer
MTAD-GAT는 두 타입의 graph attention layer인 feature oriented graph attention과 time-oriented graph attention을 사용하여 '변수 간의 관계'와 '시점 간의 관계'를 모델링합니다.
1). Feature-oriented graph attention layer
Feature-oriented graph attention layer에서는 다변량 시게열 데이터 자체를 그래프로 모델링합니다. 각 노드는 변수(서로 다른 일변량 시계열 데이터), 엣지는 변수간의 관계를 나타냅니다.
즉, 각 노드 $x_i$는 seqeuntial vector $x_i = \{x_{i,t}| t \in [0,n)\} \in \mathbb{R}^{n}$ 이며 총 $k$개의 노드가 존재합니다. $n$은 시점의 길이며 두 노드 사이의 인접 여부 혹은 관계를 나타내는 인접 행렬 $A$는 $k \times k$ 행렬입니다. 업데이트 식(update rule)은 식 $(1)$과 같습니다.

[Figure 5]는 [0:Background]에서 다루었 다변량 시계열 데이터 예제로 $v_1$의 sequential vector를 학습하는과정을 보여줍니다. 변수 $v_1$과 $v_j, j \in {2,\cdots,8}$와의 상관관계를 반영한 값인 attention score $\alpha_{12}, \cdots, \alpha_{18}$ 값과 이웃 노드 $v_j, \, j \in \{2, \cdots, 8\}$의 sequential vector를 이용하여 $v_1$의 sequential vector를 representation vector $h_1=\sigma(\sum^L_{j=1} \alpha_{1j} v_j)$으로 업데이트합니다.
Feature-oriented graph attention layer는 서로 다른 변수간의 시계열 패턴의 유사성을 기반으로 attention score를 계산하며 비슷한 시계열 패턴(sequential vector)을 가진 노드들은 학습 결과 비슷한 representation vector를 가질 것입니다.
이를 통해 feature-oriented graph attention layer는 서로 다른 변수간의 관계 바탕으로 각 노드의 sequential vector를 학습하는 것을 알 수 있습니다.
- 입력값(input)은 1-D convolution layer의 산출값(output) $\tilde{x} \in \mathbb{R}^{n \times k}$입니다.
- 산출값(output)은 $k \times n$인 행렬로 각 행은 노드의 학습된 $n$차원의 representation vector입니다.
2). Time-oriented graph attention layer
Time-oriented graph attention layer는 시계열 데이터에서 시간 의존성(temporal dependencies)을 포착합니다.
Time-oriented graph attention layer의 경우 각 sliding window에 존재하는 시점들을 그래프로 모델링합니다. 즉, 각 노드 $x_t$는 시점 $t$에 대한 feature vector $x_t = \{x_{i,t} | i \in {0, \cdots, k}\} \in \mathbb{R}^k, \, t \in \{1,2, \cdots, n\}$ 이며 엣지($A \in \mathbb{R}^{n \times n}$)는 서로 다른 시점 $t$와 $s$의 의존도를 나타냅니다. Time-oriented graph attention layer의 산출값은 $n \times k$ 행렬이며 각 행은 특정 시점의 학습된 $k$ 차원의 representation vector를 나타냅니다.
우리는 feature-oriented graph attention layer, time-oriented graph attention layer의 산출값과 1-D convolution layer의 산출값 $\tilde{\mathbf{x}}$을 concatenate합니다. 그러면 $n \times 3k$ 행렬이 만들어지며 각 행은 각 시점에 대한 서로 다른 정보가 담긴 $3k$ 차원의 feature vector를 의미합니다.
1.3 Joint Optimization
▶ Gated Recurrent Layer(GRU)
3개의 산출값을 concatenate한 $n \times 3k$ 행렬은 hidden dimension이 $d_1$인 GRU의 입력값으로 활용됩니다. GRU layer을 통해서 시계열 데이터에 존재하는 연속적인 패턴(sequential pattern)을 추정합니다.
▶ Forecasting based model & Reconstructioin based model
이전에도 얘기하였듯이 forecasting model과 reconstruction model은 각각 서로 보완적인(complementary) 뚜렷한 이점을 가지고 있습니다.
- 입력값: GRU layer의 산출값
- 산출값
- Forecasting model: 다음 시점에 대한 예측값 $\hat{x}_{i,t}, \, i \in \{1,2, \cdots, k\}, \, t \in \{1,2, \cdots, n\}$
- Reconstruction model: $\mathbf{x}$를 재건축 한 값 $\hat{\mathbf{x}}$
[Forecasting based model: Fully Connected Layer]
Forecasting model은 이전 시점 데이터 $\mathbf{x} = (x_0, x_1, \cdots, x_{n-1}), \, x_t \in \mathbb{R}^k$를 바탕으로 다음 시점 $x_{(n)} \in \mathbb{R}^k$에 대해 예측합니다. MTAD-GAT에서는 forecasting model로 hidden dimension이 $d_2$인 3개의 fully connected layer를 쌓았습니다. 손실함수로는 Root Mean Square Error(RMSE)로 식 $(2)$를 최소화하는 파라미터를 학습하는 것을 목적으로 합니다.
$$Loss_{for} = \sqrt{\sum^k_{i=1}(x_{i,n} - \hat{x}_{i,n})^2} \tag{2}$$
- $x_{i,n}$은 $x_n$의 $i^{th}$ 변수의 실제값을 나타냅니다.
- $\hat{x}_{i,n}$은 $x_{i,n}$의 forecasted based model 예측값을 나타냅니다.
[Reconstruction based model: Variational Based Auto-Encoder(VAE)]
Reconstruction based model로 variational based auto-encoder(VAE)를 사용하였으며 latent vector $z \in \mathbb{R}^{d_3}$의 주변 분포(marginal distribution)를 학습하는 것을 목표로 합니다. VAE는 전체 시계열 데이터(다변량 시계열 데이터)의 전체적인 분포를 학습하는 것을 목적으로 합니다. 입력 데이터 $\mathbf{x}$가 주어졌을 때, VAE는 조건부 분포 $p_{theta}(x|z)$로부터 $\hat{\mathbf{x}}$를 재건축합니다. 최적화 과정은 $\mathbf{x}$를 가장 잘 재건축하는 파라미터 $\theta$를 찾음으로써 다변량 시계열 데이터의 분포를 추정합니다.
$$p_{\theta}(z|x) = p_{\theta}(x|z) p_{\theta}(z)/ p_{\theta}(x) \tag{3}$$
$$p_{\theta}(x) = \int p_{\theta}(z) p_{\theta}(x|z) dz$$
- $p_{\theta}(z|x)$: 사후 분포(posterior distribution)
- $p_{\theta}(x|z)$: 가능도 함수(likelihood function)
- $p(z)$: 사전 분포(prior distribution)
식 $(3)$ 사후 분포를 계산하기 어렵기 때문에 사후 분포를 근사해서 구하기 위해 recognition model $q_{\phi}(z|x)$를 도입합니다. Recognition model(encoder) $q_{\phi}(z|x)$와 generative model(decoder) $p_{\theta}(\hat{x}|z)$가 주어졌을 때 reconstruction based loss function은 다음과 같습니다.
$$Loss_{rec} = - E_{q_{\phi}(z|x)}[logp_{\theta}(x|z)] + D_{KL}(q_{\phi}(z|x)||p_{\theta}(z) )$$
- 첫번째 식 $- E_{q_{\phi}(z|x)}[logp_{\theta}(x|z)]$은 $\mathbf{x}$의 expected negative log likelihood 식입니다.
- 두번째 식 $D_{KL}(q_{\phi}(z|x)||p_{\theta}(z) )$은 $q_{\theta}(z|x)와 $ p_{\theta}(z) $에 대한 Kullback-Leibler divergence로 regularizer 식입니다.
1.4 Model Inference
우리는 현재 각 시점 $t$별로 두 개의 결과값을 가지고 있습니다.
- Output of forecasting based model: prediction value $\{\hat{x}_i \in \mathbb{R}^n, i =1, \cdots, k\}$
- Output of reconstruction based model: reconstrucion probability $\{p_i \in \mathbb{R}^n | i = 1, \cdots, k\}$
우리는 $\hat{x}_i \in \mathbb{R}^n$와 $p_i \in \mathbb{R}^n$를 결합하여 각 시점별 이상치 점수를 산출하고자 합니다.
▶ Anomaly(Inference) score
$$\text{score} = \sum^k_{i=1}s_i = \sum^k_{i=1} \dfrac{(\hat{x}_i - x_i)^2 + \gamma \times (1-p_i)}{1 + \gamma} \in \mathbb{R}^n$$
- $s_i \in \mathbb{R}^n$: 각 변수에 대한 inference score
- $(\hat{x}_i - x_i)^2$: 예측값 $\hat{x}_i$와 실제 값 $x_i$의 차이의 제곱값으로 실제값이 예측값으로부터 얼마나 떨어져 있는지를 반영한 값
- $(1-p_i)$: reconstruction model로부터 계산되는 값으로 변수 $i$의 각 시점이 비정상 데이터일 확률값
- $k$: 변수의 총 개수
- $\gamma$: hyper-parameter
score는 각 시점별 이상치 점수가 반영된 벡터입니다.
$$y_t = \begin{cases} 1 &\text{if score}_t > \tau \\ 0 &\text{otherwise} \end{cases}, t=\{1,2,\cdots,n\}$$
MTAD-GAT는 임계값 $\tau$를 Peak Over Threshold(POT) 방법을 사용하여 선택한다고 합니다.
본 글은 다변량 시계열 이상치 탐지 방법론 중 MTAD-GAT에 대해 살펴보았습니다. 이전글에서 살펴보았던 Graph Deviation Network(GDN)은 변수 간의 관계만 고려하여 모델링하였다면 MTAD-GAT의 경우는 변수 간의 관계와 시점 간의 관계를 모두 모델링하였습니다. 또한, 이상치 점수를 forecasted based mode의 산출값과 reconstruction based model의 산출값을 결합하여 계산하였습니다. 이상으로 글을 마치도록 하겠습니다.
'Time Series Analaysis > Time Series Anomaly Detection' 카테고리의 다른 글
| Multi-Scaled Convolutional Recurrent Encoder Decoder(MSCRED) for Anomaly Detection (1) | 2024.01.30 |
|---|---|
| LSTM-based Encoder-Decoder for Multi-sensor Anomaly Detection(EncDec-AD) (0) | 2024.01.29 |
| Graph Deviation Network(GDN): 다변량 시계열 데이터 기반 이상치 탐지 방법론 (0) | 2024.01.11 |
| [SR-CNN(2)] Time Series Anomaly Detection Service at Microsoft (0) | 2024.01.03 |
| [SR-CNN (1)]: Fourier Transform (3) | 2024.01.03 |



