본 글은 다변량 시계열 데이터 이상치 기반 모델인 LSTM-based Encoder-Decoder(EncDec)에 대해 논문 [LSTM-based Encoder-Decoder for Multi-sensor Anomaly Detection(EncDec-AD)(2016)]을 바탕으로 작성하였습니다.
Long Short Term Memory Networks based Encoder-Decoder for Anomaly Detection(EncDec-AD)는 정상 시계열 데이터 재건축(reconstruct)을 목적으로 학습하며 reconstruct error를 기반으로 이상치(anomaly)를 탐지하는 모델입니다.
▶ Main Idea of EncDec-AD
- LSTM based encoder: 시계열 데이터의 입력 시퀀스(input sequence)를 고정된 차원의 vector representation으로 매핑(mapping or encoding)시킵니다.
- LSTM based decoder: 학습된 vector representaion을 기존의 입력 시퀀스(input sequence)로 재건축(decode)한 값인 target sequence를 산출합니다.
- 정상 시계열 데이터를 최대한 정확하게 재건축하기 위해서 학습 시 오직 '정상' 데이터로만 학습합니다(EncDec-AD는 학습 시 오직 정상 데이터만 사용합합니다).
- Test 시, 비정상 데이터(abnormal data)가 입력된 경우 재건축이 잘 안 될 것이며 reconsturction error 값도 크게 나올 것입니다.
본격적으로 EncDec-AD의 방법론(methodology)에 대해 설명하겠습니다.
0. Problem Setting
▶ Problem Definition
총 시점(timestamp)의 길이는 $L$, 총 변수의 개수는 $m$개인 다변량 시계열 데이터 $\mathbf{X}$를 다루도록 하겠습니다.
※ 다만, large dataset에 대해서는 window size를 $L$로 명시하겠습니다.
$$\mathbf{X} = (\mathbf{x}^{(1)}, \mathbf{x}^{(2)}, \cdots, \mathbf{x}^{(L)}), \, \mathbf{x}^{(i)} \in \mathbb{R}^{m}$$
▶ Process
[Step 1]. 정상 시계열 데이터(normal data)를 재건축(reconstruct)하는 LSTM Encoder-Decoder 모델을 학습합니다.
[Step 2]. Reconstruction error(재건축 오류)는 각 시점 $\mathbf{x}^{(i)}$가 비정상일 가능성에 대해 계산할 때 사용됩니다. 즉, anomaly score(이상치 점수) $a^{(i)}$를 계산하는데 사용됩니다.
- Anomaly score $a^{(i)}$가 높을수록 시점 $i$는 비정상일 가능성이 높다는 것을 의미합니다.
1. LSTM Encoder-Decoder as reconstruction model
우리는 정상 시계열 데이터를 재건축하는 것을 목적으로 LSTM Encoder-Decoder 모델을 학습합니다.
※ Long Short Term Memory(LSTM)에 대한 자세한 내용은 아래 두 블로그를 참조하시면 좋을것 같습니다.
Recurrent Neural Network(RNN), Long Short Term Memory(LSTM)
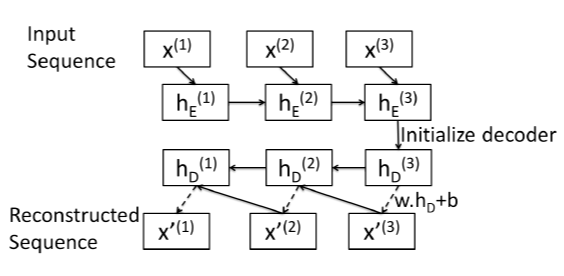
[ LSTM Encoder ]
$i \in \{1, 2, \cdots, L\}$에 대해서
- input: $\mathbf{x}^{(i)}, \, h^{(i-1)}_E(h^{(0)}_E = 0)$
- output: 각 시점 $i$에 대한 산출값 $y^{(i)}$, hidden state(은닉 상태) $h^{(i)}_E \in \mathbb{R}^c$
- $c$: hidden layer의 노드(뉴런)의 개수
- 순차적으로 현재 시점의 새로운 입력값 $x^{(i)}$와 과거 정보(hidden state) $h_E^{(i-1)}$를 입력받아 새로운 정보 $h^{(i)}_E$를 업데이트합니다.
- $h^{(i)}$에는 hidden state 정보뿐만 아니라 cell state 정보도 함께 고려되어 있습니다.
즉, LSTM Encoder에서는 input time series $X$의 vector represpentation $h_E$를 학습합니다.
[ LSTM Decoder ]
LSTM Decoder에서는 입력 시퀀스의 역순 $\{x^{(L)}, x^{(L-1)}, \cdots, x^{(1) }\}$으로 각 시점을 재건축(reconstruct)합니다. 또한, LSTM Encoder에서는 초기 은닉 값(initial hidden state) $h^{(0)}_E$를 0으로 초기화하여 사용하는 반면 LSTM Decoder의 초기 은닉 값 $h_D^{(L)}$으로는 LSTM Encoder의 마지막 은닉 값(last hidden state) $h^{(L)}_E$을 사용합니다($h_D^{(L)} = h^{(L)}_E$). $h^{(L)}_D$를 사용하여 선형 층(linear layer, $W \cdot h^{(L)}_D + b$)을 이용하여 시점 $L$의 input time series $\hat{x}^{(L)}$ 예측합니다.
$i \in \{1, 2, \cdots, L\}$에 대해서
- input: $\mathbf{x}^{(i+1)}, \, h^{(i+1)}_E$
- output: 각 시점 $i$에 대한 재건축(reconstruct)된 입력값 $\hat{x}^{(i)}$와 hidden state(은닉 상태) $h^{(i)}_E \in \mathbb{R}^c$
[참고]
모델에 대한 보충자료로 [Figure 1]과 LSTM Encoder, LSTM Decoder의 코드를 첨부하였습니다.
import torch
import torch.nn as nn
from torch.autograd import Variableclass Encoder(nn.Module):
def __init__(self, input_size=29, hidden_size=128, output_size=29, num_layers=2):
super(Encoder, self).__init__()
self.hidden_size = hidden_size
self.num_layers = num_layers
self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True, dropout=0.1, bidirectional=False)
## batch_first=True로 설정하였기 때문에
## (batch_size, sequene length, input_size) 이와 같이 설정해주어야 합니다.
self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
def forward(self,x):
## hidden state와 cell state는 모두 0으로 초기화합니다.
h_0 = Variable(torch.zeros(self.num_layers, x.size(0), self.hidden_size)).to(self.device)
c_0 = Variable(torch.zeros(self.num_layers, x.size(0), self.hidden_size)).to(self.device)
output, (hn, cn) = self.lstm(x, (h_0,c_0))
return (hn, cn)class Decoder(nn.Module):
def __init__(self, input_size=29, hidden_size=128, output_size=29, num_layers=2):
super(Decoder, self).__init__()
self.hidden_size = hidden_size
self.output_size = output_size
self.num_layers = num_layers
self.lstm = nn.LSTM(input_size, hidden_size, num_layers, batch_first=True, dropout=0.1, bidirectional=False)
self.relu = nn.ReLU()
self.fc = nn.Linear(hidden_size, output_size)
def forward(self, x, hidden):
## decoder의 초기 hidden state와 cell state는 encoder의 마지막 hidden state와 cell state 값입니다.
hn, cn = hidden
output, (hn, cn) = self.lstm(x, (hn, cn))
prediction = self.fc(output)
return prediction, (hn,cn)class LSTMAutoEncoder(nn.Module):
def __init__(self, input_dim: int=29, latent_dim: int=128, window_size: int=64, **kwargs) -> None:
super(LSTMAutoEncoder, self).__init__()
self.latent_dim = latent_dim
self.input_dim = input_dim
self.window_size = window_size
self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
if "num_layers" in kwargs:
num_layers = kwargs.pop("num_layers")
else:
num_layers = 1
self.encoder = Encoder(
input_size = input_dim,
hidden_size = latent_dim,
num_layers = num_layers)
self.reconstruct_decoder = Decoder(
input_size = input_dim,
output_size = input_dim,
hidden_size = latent_dim,
num_layers = num_layers)
def forward(self,x,**kwargs):
batch_size, sequence_length, var_length = x.size()
## Encoder
encoder_hidden = self.encoder(x) ## return: (hidden, cell)
## decoder의 경우, 시간 역순으로 예측
inv_idx = torch.arange(sequence_length-1,-1,-1).long() ## 시간 역순 배열
reconstruct_output = []
temp_input = torch.zeros((batch_size, 1, var_length), dtype=torch.float).to(self.device)
## encoder의 마지막 hidden state는 decoder의 초기 hidden state로 사용
hn = encoder_hidden
for t in range(sequence_length):
temp_input, hn = self.reconstruct_decoder(temp_input, hn) ## hidden = (hidden, cell)
## temp_input = 각 input time series를 재건축 한 값
reconstruct_output.append(temp_input)
reconstruct_output = torch.cat(reconstruct_output, dim=1)[:, inv_idx, :]
return reconstruct_output2. Train and Calculate Anomaly Score
▶ 훈련 데이터셋 / 검증 데이터셋 / 테스트 검증데이터셋

정상 시계열 데이터의 경우 크게 4개의 집합으로 분할하였습니다.
- $s_N$: 훈련 데이터셋
- $v_{N1}$: 학습 조기 종료를 위해 사용되는 데이터셋 및 정상 시계열 데이터의 분포(평균, 분산)을 계산하기 위해 사용되는 데이터셋
- $v_{N2}$: 검증 데이터셋
- $t_N$: 테스트 데이터셋
비정상 데이터의 경우는 크게 2개의 집합으로 분할하였습니다.
- $v_{A}$: 검증 데이터셋
- $t_{A}$: 테스트 데이터셋
▶ 손실 함수(loss function)
손실 함수로는 Mean Sqaured Error(MSE) loss를 사용하였습니다.
$$\sum_{\mathbf{X} \in s_N} \sum^L_{i=1} || \mathbf{x}^{(i)} - \hat{\mathbf{x}}^{(i)} ||^2 \tag{(1)}$$
- $s_{N}$: normal training sequence의 집합
최적화 과정을 통해 식 $(1)$을 최소화하는 파라미터를 찾습니다.
▶ Anomaly score $a^{(i)}$ 계산
[Reconstruction error vector 계산]
검증 및 테스트 과정에서 각 시점에 대한 reconstruction error(식 $(2)$)를 산출합니다.
$$e^{(i)} = |\mathbf{x}^{(i)} - \hat{\mathbf{x}}^{(i)}|$$
Reconstruction error vector가 평균이 $\mathbf{\mu}$, 분산이 $\mathbf{\Sigma}$인 정규분포(Normal distribution)를 따른다고 가정하겠습니다. 집합 $v_{N1}$에 속하는 각 시점의 reconstruction error vector의 $\mathbf{\mu}$ 및 $\mathbf{\Sigma}$를 Maximum Likelihood Estimation(MLE)로 추정합니다.
[Anomaly Score 계산]
정상 시계열 데이터의 reconstruction error vector로부터 추정된 $ \mathbf{\hat{\mu}} $, $\mathbf{\hat{\Sigma}} $를 토대로 anomaly score (식 $(3)$)을 계산합니다.
$$a^{(i)} = (e^{(i)}-\mathbf{\hat{\mu}})^T \mathbf{\hat{\Sigma}}^{-1}(e^{(i)}- \mathbf{\hat{\mu}}) \tag{(3)}$$
만약, 임의의 임계값(threshold) $\tau$에 대해서
- $a^{(i)} < \tau$인 경우, 정상 데이터로 판단합니다.
- $a^{(i)} > \tau$인 경우, 비정상 데이터로 판단합니다.
본 글은 자연어처리 모델로 제안된 LSTM based Encoder-Decoder를 anomaly detection에 적용하여 시계열 데이터에서 비정상 데이터(change point)를 탐지하는 방법을 설명하였습니다. 다음 글에서는 서로 다른 시점간의 내적 계산(pairwise inner product)을 통해 산출된 유사도를 원소로 갖는 signature matrix를 생성해 Convolution Encoder -> ConvLSTM -> Convolution Decoder를 통해 시계열 데이터에서 비정상 데이터를 탐지하는 방법을 다루고자 합니다.



