본 글에서는 Long Short Term Memory(LSTM)에 대해 살펴보도록 하겠습니다. 이전글에서 살펴보았던 Recurrent Neural Network(RNN)은 파라미터(parameter)가 업데이트 되는 과정에서 기울기가 1보다 작은 값이 계속 곱해짐으로써 기울기가 사라지는 기울기 소멸 문제( vanishing gradient problem)가 존재합니다. 이에 대한 해결방안으로 LSTM은 은닉층의 각 노드(혹은 뉴런)에 망각 게이트(forget gate), 입력 게이트(input gate), 출력 게이트(output gate)라는 새로운 요소를 추가하였습니다.
※ 그림 참고자료: Understading LSTM networks



▶ LSTM의 key point

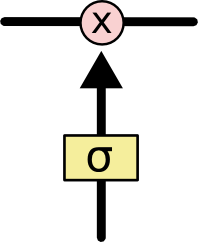
- 망각 게이트(forget gate), 입력 게이트(input gate), 출력 게이트(output gate)
- cell state(CtCt)
- [Figure 2-1] 참조
LSTM은 게이트(gate)에 의해 정보의 흐름이 조절되며 cell state에 정보를 제거하거나 추가하는 능력이 있습니다. 각 게이트(gate)는 sigmoid neural net layer과 pointwise multiplication operation으로 구성되어 있습니다([Figure 2-2] 참조). Sigmoid layer는 과거 정보 및 현재 정보를 얼마만큼 반영할지에 대하여, 즉, 반영하고자하는 정보의 비중에 대한 값으로 00과 11 사이의 확률 값을 출력합니다.
- 산출값(output)이 00인 경우 어떠한 값도 통과시키지 않는다는 것을 의미합니다.
- 산출값(output)이 11인 경우 모든 정보를 통과시킨다는 것을 의미합니다.
LSTM 구성요소 3가지의 gate와 cell state의 자세한 내용을 본격적으로 [Section 1: LSTM 순전파]에서 살펴보고자 합니다.
1. LSTM 순전파
1.1 망각 게이트(forget gate)
과거의 정보를 어느 정도 기억할 것인가?
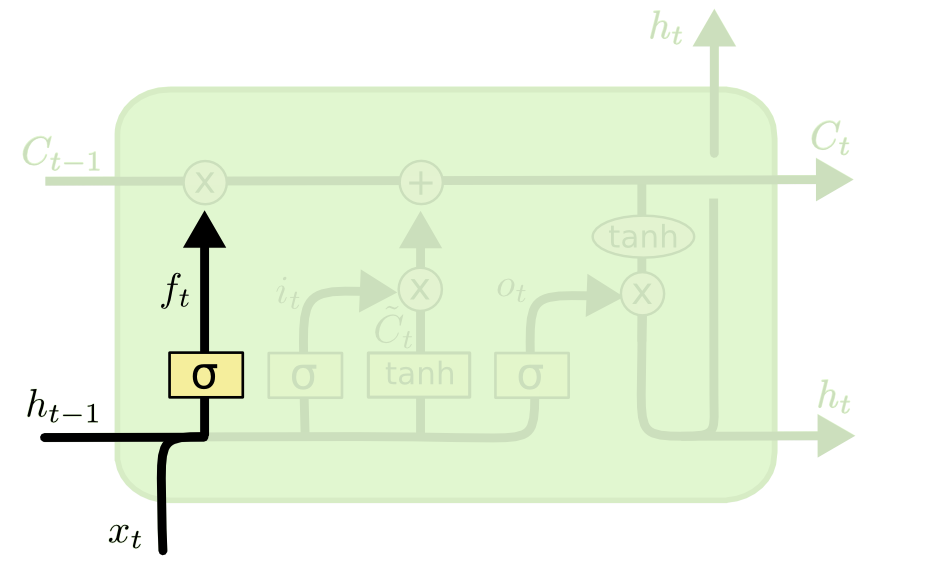
ft=σ(Wfht−1+Wfxt+bf)ft=σ(Wfht−1+Wfxt+bf)
- input: 과거의 정보 ht−1ht−1, 새로운 입력값 xtxt
- output: 과거의 정보를 반영하는 비중 ft∈(0,1)ft∈(0,1)
- σσ: sigmoid function
과거의 정보 ht−1ht−1과 현재 정보 xtxt를 이용하여 이전 상태의 정보를 현재 메모리(CtCt)에 얼만큼 반영할지 혹은 과거의 정보를 얼마나 지울지(망각할지)를 결정하는 역할을 합니다.
- ft=1ft=1인 경우, 이전 시점까지의 메모리 Ct−1Ct−1을 그대로 반영한다는 것을 의미합니다.
- ft=0ft=0인 경우, 이전 시점까지의 메모리 Ct−1Ct−1에 대한 정보를 모두 초기화(reset)한다는 것을 의미합니다.
1.2 입력 게이트(input gate)
현재 정보(새로운 정보)를 어느 정도 기억할 것인가?
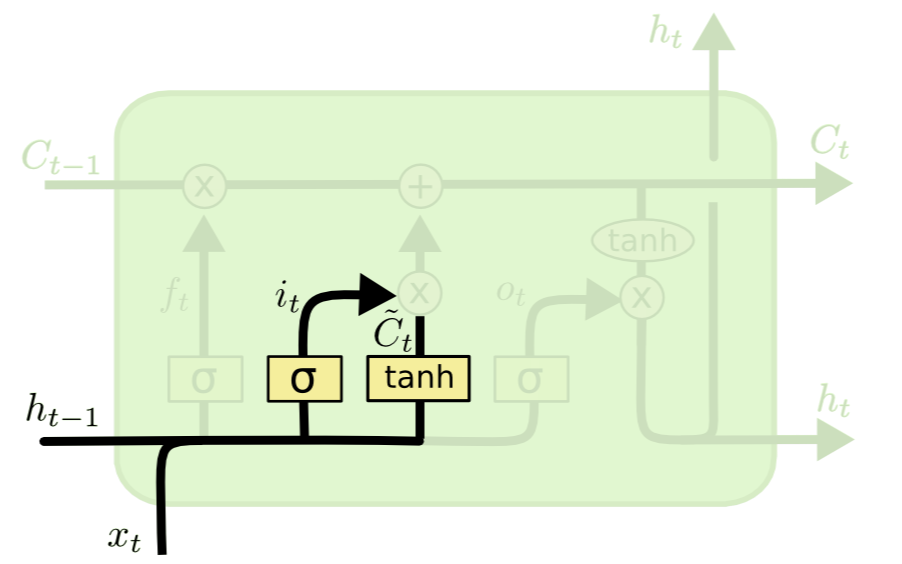
[Input gate layer]
it=σ(Wiht−1+Wixt+bi)it=σ(Wiht−1+Wixt+bi)
- input: 과거의 정보 ht−1, 새로운 입력값 xt
- output: 현재의 정보를 반영하는 비중 it∈(0,1)
[Tanh layer]
˜Ct=tanh(Wcht−1+Wcxt+bc)
-
- input: 과거의 정보 ht−1, 새로운 입력값 xt
- output: new candidate values ˜Ct
입력 게이트는 현재 정보(새로운 정보)를 Ct에 얼만큼 반영할지를 결정하는 부분으로 크게 두 파트인 input gate layer와 tanh layer로 나눌 수 있습니다. Input gate layer는 sigmoid layer로 현재 정보를 반영하는 비중을 계산합니다.
- it=1이면, 현재 정보 xt가 들어올 수 있도록 허용(open)한다는 것을 의미합니다.
- it=0이면, 새로운 정보 xt에 대한 유입을 차단하겠다는 것을 의미합니다.
Tanh layer는 과거 정보 ht−1과 새로운 정보 xt를 이용하여 시점 t에서 새로 업데이트된 요약된 정보(기억) ˜Ct를 산출하는 식입니다. it∗˜Ct 계산을 통해 현재 새로 업데이트된 정보를 Ct에 얼만큼 반영할지를 정합니다.
1.3 셀(Cell)
Cell Update
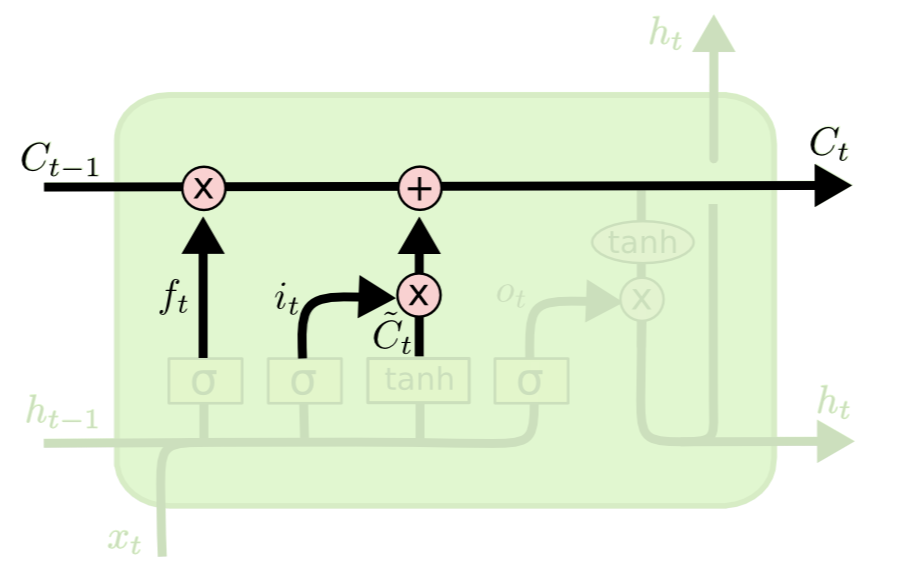
Ct=ft⋅Ct−1+it⋅˜Ct
- Ct−1: old cell state
- ft∈(0,1): 과거 정보 반영 비중
- ˜Ct: new information(새로 업데이트된 정보)
- it∈(0,1): 현재 정보(새로운 정보) 반영 비중
Old cell state Ct−1에 과거 정보 반영 비중 ft의 곱과 new information ˜Ct에 현재 정보의 반영 비중 it의 합을 통해 new cell state Ct를 계산합니다. 즉, 셀은 과거 정보와 현재 정보의 비중을 적절하게 조절하여 업데이트 됩니다. 이렇게 LSTM은 셀을 정의하여 장기 및 단기 기억이 가능합니다.
1.4 출력 게이트(Output gate)
최종적으로 현재 시점 t에 대하여 어떤 정보 ht를 출력할 것인가?
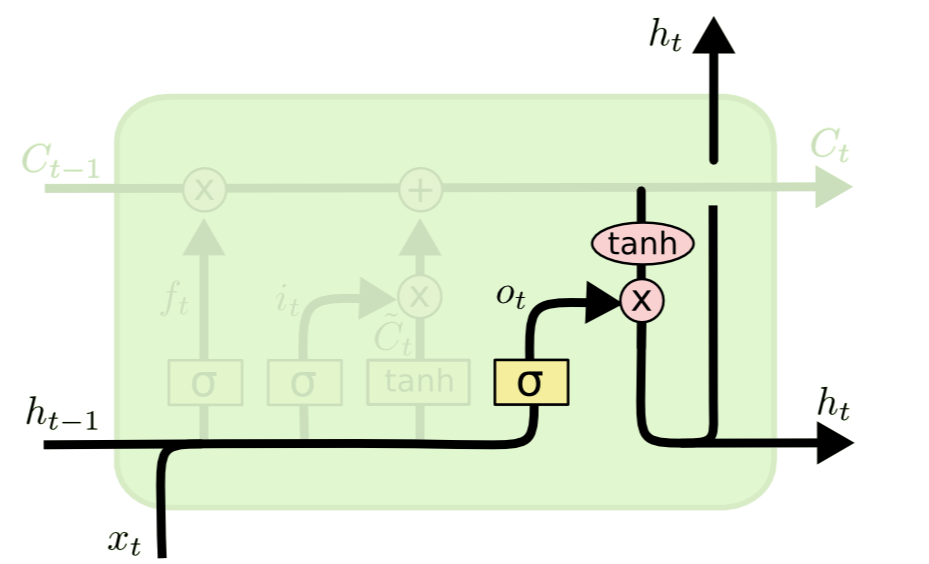
ot=σ(Woht−1+Woxt+bo)
- input: 과거의 정보 ht−1, 새로운 입력값 xt
- output: cell state의 어떤 정보(부분)을 반영할지에 대한 비중 ot∈(0,1)
ht=ottanh(Ct)
- ht: 입력값 ht−1과 xt에 대한 최종 출력값(output)
출력 게이트(output gate)는 과거 정보와 현재 정보의 비중을 적절하게 조절하여 반영된 메모리 Ct의 정보를 그대로 모두 출력하는 것이 아닌 어떤 정보를 반영할지에 대한 비중 ot을 계산하는 부분입니다. 즉, 출력 게이트를 통해 계산된 ot를 이용하여 output ht는 cell_state의 특정 정보만을 출력합니다.
- ot=1인 경우, 현재 cell state Ct가 의미 있는 정보를 담고 있다고 판단하여 그대로 최종 출력합니다.
- ot=0인 경우, 현재 cell state Ct에 대한 어떠한 정보도 출력하지 않으며 모두 0 값을 갖습니다.
▶ [LSTM 순전파 학습 단계 정리]
LSTM은 망각 게이트, 입력 게이트를 기반으로 셀 메모리 Ct를 업데이트합니다. 출력 게이트와 업데이트된 셀 메모리 Ct를 이용하여 최종적으로 출력값 ht를 계산합니다. 입력 길이만큼 이와 같은 과정이 반복되며 최종적으로 backpropagation을 통해 파라미터가 업데이트는 과정을 [Section 2: LSTM 역전파]에서 살펴보겠습니다.
2. LSTM 역전파
LSTM은 cell Ct을 통해서 역전파(backpropagation)을 수행하기 때문에 '중단 없는 기울기(uninterrupted gradient flow)'라고 합니다.
※ 최종 오차는 모든 노드에 전파되는데 이때 cell을 통해서 중단 없이 전파되기 때문에 붙여진 이름입니다.
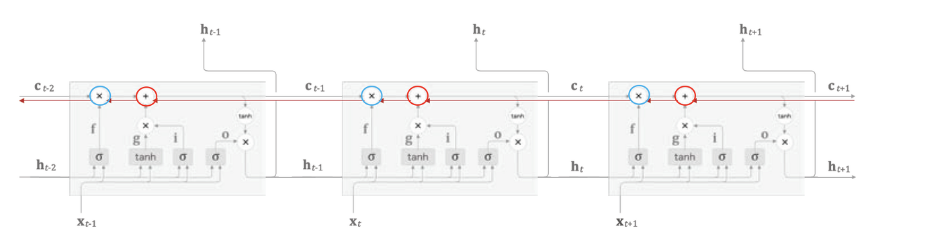
▶ 기울기 소실 문제 해결방법
빨간색 선(red line)은 셀 Ct을 통해서 역전파 되어가는 과정을 나타냅니다. 빨간색 선(red line)을 살펴보면 오직 2개의 연산((+), (×))만이 역전파 수행에 관여하는 것을 볼 수 있습니다.
- (+)는 덧셈 연산이기 때문에 gradient 계산에 관여하지 않습니다. 즉, 기울기의 변화가 일어나지 않기 때문에 기울기 소실 문제 발생 가능성이 낮아집니다.
- (×)는 행렬 연산이 아닌 pointwise multiplication(원소별 곱셈)입니다. RNN의 기울기 소실 원인 중 하나가 행렬 연산에 의해서도 존재하는데 LSTM의 경우 pointwise multiplication으로 수행하기 때문에 이 연산에서도 기울기 소실 문제 발생 가능성을 낮추었습니다.
▶ Update Parameter
셀 단위로 오차가 전파된다고 해서 입력 방향으로 오차가 전파되지 않는 것은 아닙니다. 역전파 계산에 관여된 망각 게이트 f, 입력 게이트 i, 출력 게이트 o 모두 매 iteration마다 달라지며 모든 게이트 값들이 학습 데이터를 통해 갱신되는 파라미터 Wf,Wi,Wc를 통해 최적의 게이트를 찾아갑니다.
3. LSTM 구현코드
LSTM 구현코드는 이론에 대한 이해를 돕고자 참고자료로 넣었습니다.
3.1 LSTM 셀 구현코드
class LSTMCell(nn.Module):
def __init__(self, input_size, hidden_size, bias=True):
super(LSTMCell, self).__init__()
self.input_size = input_size
self.hidden_size = hidden_size
self.bias = bias
self.x2h = nn.Linear(input_size, 4*hidden_size, bias=bias) ## 새로운 값 입력
self.h2h = nn.Linear(hidden_size, 4*hidden_size, bias=bias)
## 4를 곱해주는 이유는 LSTM에서의 중요한 게이트 4개 => 망각 게이트, 입력 게이트, 셀 게이트, 출력 게이트 => 모든 게이트를 한 번에 구하기
## 추후에 계산된 게이트를 gates.chunk(4,1)에 의해 네 개로 쪼개져서 각각 망각, 입력, 셀, 출력 게이트를 의미하는 변수에 저장
## 결국에는 gates가 4개로 쪼개지는 상황이기 때문에 4 가 곱해졌던 것
self.reset_parameters()
## 모델 파라미터 초기화
def reset_parameters(self):
std = 1.0/math.sqrt(self.hidden_size)
for w in self.parameters():
w.data.uniform_(-std,std)
def forward(self, x, hidden):
hx, cx = hidden ## h_{t-1}, c_{t-1}
x = x.view(-1, x.size(1))
gates = self.x2h(x) + self.h2h(hx) ## 모든 gate의 input값: 현재 데이터 + 이전 과거의 요약된 정보
gates = gates.squeeze() ## 텐서의 차원 축소, 1의 값을 갖는 차원을 제거
ingate, foregate, cellgate, outgate = gates.chunk(4,1)
ingate = F.sigmoid(ingate)
foregate = F.sigmoid(foregate)
cellgate = F.tanh(cellgate)
outgate = F.sigmoid(outgate)
cy = torch.mul(cx, foregate) + torch.mul(ingate, cellgate)
hy = torch.mul(outgate, F.tanh(cy))
return (hy, cy)3.2 LSTM 모델 구현코드
class LSTMModel(nn.Module):
def __init__(self, input_dim, hidden_dim, layer_dim, output_dim, bias=True):
super(LSTMModel, self).__init__()
self.hidden_dim = hidden_dim ## 은닉층의 뉴런의 개수
self.layer_dim = layer_dim ## 은닉층의 개수
self.lstm = LSTMCell(input_dim, hidden_dim, layer_dim)
self.fc = nn.Linear(hidden_dim, output_dim)
def forward(self,x):
if torch.cuda.is_available():
h0 = Variable(torch.zeros(self.layer_dim, x.size(0), self.hidden_dim).cuda())
else:
h0 = Variable(torch.zeros(self.layer_dim, x.size(0), self.hidden_dim))
if torch.cuda.is_available():
c0 = Variable(torch.zeros(self.layer_dim, x_zie(0), self.hidden_dim).cuda())
else:
c0 = Variable(torch.zeros(self.layer_dim, x.size(0), self.hidden_dim))
outs = []
cn = c0[0,:,:]
hn = h0[0,:,:]
for seq in range(x.size(1)):
hn, cn = self.lstm(x[:,seq,:], (hn,cn))
outs.append(hn)
out = outs[-1].squeeze()
out = self.fc(out)
return out본 글에서는 RNN의 변형 형태인 LSTM에 대해서 살펴보았습니다. 다음글에서는 파라미터의 개수가 많은 단점을 가진 LSTM을 보완한 Gated Recurrent Unit에 대해 살펴보고자 합니다.
'Time Series Analaysis > Time Series Analysis' 카테고리의 다른 글
| Linear Gaussian State Space Model (0) | 2024.06.10 |
|---|---|
| Convolutional LSTM network(ConvLSTM) (0) | 2024.01.29 |
| Gated Recurrent Unit(GRU) (2) | 2024.01.23 |
| Recurrent Neural Network(RNN) (0) | 2024.01.22 |



