본 글에서는 State Space Model 중 Gaussian State Space Model에 대해 살펴보고자 합니다.
[참고자료]
- Time Series Analysis and Its Applications
- Linear Gaussian State Space Model
- Stanford Lecture Note: Linear Gaussian State Space Model
1. State Space Model(SSM)
상태 공간 모형(State Space Model)은 시계열 데이터 모형으로 크게 상태 방정식(state equation)과 관측 방정식(observation equation)으로 이루어집니다.
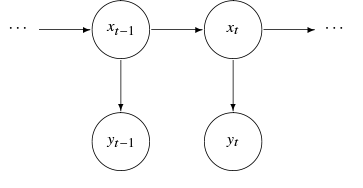
▶ 상태 방정식(state equation)
- $x_t$: state process(hidden or latent process)로 관측되지 않는 데이터(""unobserved data"")입니다.
- $x_t$에 대한 가정: Markov Process
Markov Process는 과거와 현재 상태가 주어졌을 때의 미래 상태의 조건부 확률 분포가 과거 상태와는 독립적으로 현재 상태에 의해서만 결정된다는 것을 의미합니다. 즉, $t+1$ 시점은 오직 $t$ 시점에만 의존합니다(dependent).
$$P(x_{t+1}|x_t, x_{t-1}, \cdots, x_0) = P(x_{t+1}|x_t)$$
따라서, $x_t$에 대한 모형 설정으로 AR(1) 모형 혹은 ARMA(1,1) 모형 등을 생각할 수 있다.
본 글에서는 ARMAX(1,1) 모형으로 설정하겠습니다.
※ 시계열 통계 모형 참고자료(AR, MA, ARMA, ARMAX)
$$x_t = \Phi x_{t-1} + \gamma u_t + w_t$$
▶ 관측 방정식(observation equation)
$$y_t = A_t x_t + \Gamma u_t + v_t$$
$y_t$는 우리가 실제로 관측한 데이터입니다.
우리는 state vector $x_t \in \mathbb{R}^p$에 대해서 직접적으로 관측할 수는 없지만,
observation vector $y_t \in \mathbb{R}^q$를 통해 간접적으로 관측할 수 있습니다.
▶ State Space Model의 목표
State Space Model의 목표는 observation vector $y_{1:s} = \{y_1,y_2, \cdots, y_s\}$를 기반으로 $x_t$를 추정하는 것입니다.
- $s<t$
- $s=t$
- $s>t$
A primary aim of state space model, would be to produce estimators for the underlying unobserved signal $x_t$, given the data $y_{1:s} = \{y_1, \cdots, y_n\}$(⇒ observed data)
Noise vector $w_t$와 $v_t$가 정규분포(Normal distribution)을 따르는 경우,
우리는 Gaussian State Space Model이라고 지칭합니다.
2. Gaussian State Space Model(GSSM)
▶ 상태 방정식(state equation)
$$x_t = \Phi x_{t-1} + \gamma u_t + w_t \in \mathbb{R}^p \tag{1}$$
- $w_t \stackrel{iid}{\sim} \mathbf{\color{darkred}{N_p(0, Q)}} \in \mathbb{R}^p, \, Q \in \mathbb{R}^{p \times p}$
- $u_t \in \mathbb{R}^p$: fixed input, exogenous variables(파생변수)
- $x_0 \sim \mathbf{\color{darkred}{N_p(\mu_0, \Sigma_0)}}$
정규분포의 성질에 의해 $x_t, \, t \in \{1,2,\cdots T\}$는 모두 정규분포를 따릅니다.
▶ 관측 방정식(observation equation)
$$y_t = A_t x_t + \Gamma u_t + v_t \in \mathbb{R}^q \tag{2}$$
- $A_t \in \mathbb{R}^{q \times p}$: measurement or observation matrix
- $v_t \stackrel{iid}{\sim} \mathbf{\color{darkred}{N_q(0, R)}} \in \mathbb{R}^{q}, \, R \in \mathbb{R}^{q \times q}$
마찬가지로 정규분포의 성질에 의해 $y_t, \, t \in \{1,2,\cdots, T\}$도 정규분포를 따릅니다.
▶ Assumption
- $x_{0}, \, \{w_t\}, \{v_t\}$는 모두 독립이다.
- 이 가정은 필수는 아닙니다.
▶ Estimation of parameter $\theta$
현재 우리가 추정해야 하는 파라미터는 $\theta = (\Phi, \gamma, A_t, \Gamma, Q,\Sigma_0, R)$입니다.
파라미터 추정 방법으로 Expectation Maximize(EM) 알고리즘과 Markov Chain Monte Carlo(MCMC) 방법이 존재합니다.
현재 모수 $\theta$ 추정까지 완료된 상태에서
State Space Model의 목적인 $y_{1:s} = \{y_1,y_2,\cdots,y_s\}$가 주어졌을 때 $x_t$를 추정하는 방법에 대해 살펴보고자 합니다.
▶ Filtering v.s. Smoothing v.s. Forecasting
인덱스 $s$와 $t$에 따른 다음 3가지의 문제를 정의하고자 합니다.
- $s<t$인 경우: forecasting or prediction
- $s=t$인 경우: filtering
- $s>t$인 경우: smoothing
즉, $P(x_{t+1}|y_{1:t})$는 prediction distribution, $P(x_{t+1}|y_{t+1})$는 filtered distribution, $P(x_{t+1}|y_{1:T})$는 smoothed distribution이라고 지칭하겠습니다.
또한, 우리는 식 $(1)$과 식 $(2)$에서 정규분포를 가정했기 때문에 prediction distribution, filtered distribution, smoothed distribution 모두 정규분포를 따릅니다.
- $x_{t+1}|y_{1:t} \sim N$
- $x_{t+1}|y_{t+1} \sim N$
- $x_{t+1}|y_{1:T} \sim N$
▶ Kalman Filter v.s Smoothing
[1]. Kalman Filter
이전 관측치 $y_{1:t}$를 사용하지 않고,
새로운 데이터 $y_{t+1}$가 주어졌을 때, filter distribution $P(x_{t}|y_{t})$을 $P(x_{t+1}|y_{t+1})$로 업데이트 할 때 Kalman Filter 방법론을 사용합니다.
→ $x_{t+1}|y_{t+1}$가 정규분포를 따르는 것은 알고 있으며 정규분포의 모수인 평균과 분산을 Kalman Filter를 통해 구하고자 하는 것
[2]. (Rausch - Tung - Streinbel, RTS) Smoothing
$P(x_{t+1}|y_{1:T})$가 주어졌을 때, $P(x_{t}|y_{1:T})$를 예측할 때 Smoothing 방법론을 사용합니다.
즉, 이전 hidden state에 대해 예측하는 것입니다.
→ $x_{t+1}|y_{1:T}$의 평균과 분산을 구하고자 하는 것
먼저, Kalman Filter에 대해 알아보겠습니다.
2.1 Kalman Filter
▶Define problem
$$ \text{Calculate distribution of } x_{t+1}|y_{t+1} $$
$$x_{t+1}|y_{t+1} \sim N(?,?)$$
▶Kalman Filter의 구성요소
Kalman Filter는 크게 두 단계로 이루어져 있습니다.
- "Time Update"
- "Measurement Upate"
2.1.1 Time Update
▶ Purpose
마지막으로 업데이트 된 filtered distribution $P(x_t|y_{1:t})$가 주어졌을 때,
prediction distribution $P(x_{t+1}|y_{1:t})$을 계산하는 것이 Time Update의 목적입니다.
▶ Notation
$xt|y_{1:s}$에 대한 기댓값과 공분산을 다음과 같이 명시하겠습니다.
$$\hat{x}_{t|s} = E(x_t|y_{1:s}) \tag{a}$$
$$\begin{align*}
P_{t1,t2|s} &= E[(x_{t1|s} - \hat{x}_{t1|s})(x_{t2|s} - \hat{x}_{t2|s})|y_{1:s}] \\ &= E[(x_{t1|s} - \hat{x}_{t1|s})(x_{t2} - \hat{x}_{t2|s}) | y_{1:s}]\end{align*} \tag{b}$$
▶ Compute mean of $x_{t+1}|y_{1:t}$
$$\begin{align*}
\mathbf{\color{darkred}{\hat{x}_{t+1|t}}} &= E[x_{t+1}|y_{1:t}] \\ &= E[\Phi x_t + \gamma u_t + w_t] (\because (1))\\ &= E[\Phi x_t|y_{1:t}] + E[\gamma u_t |y_{1:t}] + E[w_t|y_{1:t}] \\ &= \mathbf{\color{darkred}{\Phi \hat{x}_{t|t} + \gamma u_t}} \end{align*}$$
- $\hat{x}_{t|t} = E[x_t|y_{1:t}]$
- $u_t$는 고정된 값이므로, $E[\gamma u_t|y_{1:t}] = \gamma u_t$
- $w_t \perp y_{1:t} \to E[w_t|y_{1:t}] = E[w_t] = 0$
▶ Compute covariance of $x_{t+1}|y_{1:t}$
$$\begin{align*}
\mathbf{\color{darkred}{P_{t+1|t}}}= Var(x_{t+1}|y_{1:t}) &= Var(\Phi x_t + \gamma u_t + w_t|y_{1:t}) \\ &= Var[\Phi x_t|y_{1:t}] + Var[w_t|y_{1:t}] \\ &= \Phi Var[x_t|y_{1:t}]\Phi^T + Q
\\ &= \mathbf{\color{darkred}{\Phi P_{t|t} \Phi^T + Q}}
\end{align*}$$
- $P_{t|t} = Var[x_t|y_{1:t}]$
- $x_t \perp w_t \to Cov(x_t, w_t |y_{1:t})=0$
- $w_t \perp y_{1:t} \to Var(w_t | y_{1:t}) = Var(w_t) = Q$
▶ Distribution of $x_{t+1}|y_{1:t}$
$$x_{t+1}|y_{1:t} \sim N(\hat{x}_{t+1}|t, P_{t+1|t})$$
- $\hat{x}_{t+1} = \Phi \hat{x}_{t|t} + \gamma u_t$
- $P_{t+1|t} = \Phi P_{t|t} \Phi^T + Q$
2.1.2 Measurement Update
▶ Purpose
마지막으로 업데이트 된 prediction distribution $P(x_{t+1}|y_{1:t})$가 주어졌을 때,
filtered distribution $P(x_{t+1}|y_{t+1})$을 계산하는 것이 Measurement Update의 목적입니다.
▶ Step
Measurement Update는 크게 2단계로 이루어집니다.
- calculate joint distribution of $y_{t+1},x_{t+1}|y_{1:t}$
- calculate conditional distribution of $x_{t+1}|y_{t+1}$
▷ First step: calculate the joint distribution of $y_{t+1}, x_{t+1}|y_{1:t}$
우리가 계산해야 하는 값은 다음과 같습니다.
- $E[y_{t+1}|y_{1:t}]$, $Cov(y_{t+1}, y_{t+1}|y_{1:t})$ → unknown value
- $E[x_{t+1}|y_{1:t}] = \hat{x}_{t+1|t}$, $Cov(x_{t+1}, x_{t+1}|y_{1:t}) = P_{t+1|t}$ → known value(Time Update에서 구한 값)
- $Cov(y_{t+1},x_{t+1}|y_{1:t})$ → unknown value
[1]. calculate the $E[y_{t+1}|y_{1:t}]$, $Cov(y_{t+1}, y_{t+1}|y_{1:t})$
$$\begin{align*}
\mathbf{\color{darkred}{\hat{y}_{t+1|t}}} &= E[y_{t+1}|y_{1:t}] \\ &= E[A_{t+1}x_{t+1} + \Gamma u_{t+1} + v_{t+1} |y_{1:t}] \\ &= A_{t+1} E[x_{t+1}|y_{1:t}] + \Gamma u_{t+1} \\ &= \mathbf{\color{darkred}{A_{t+1} \hat{x}_{t+1|t} + \Gamma u_{t+1}}}
\end{align*}
$$
$$
\begin{align*}
\mathbf{\color{darkred}{Cov(y_{t+1}, y_{t+1}|y_{1:t})}} &= E[(y_{t+1} - \hat{y}_{t+1|t})(y_{t+1} - \hat{y}_{t+1|t})^T|y_{1:t}] \\ &=E[(A_{t+1}x_{t+1} + v_{t+1} - A_{t+1}\hat{x}_{t+1|t})(A_{t+1}x_{t+1} + v_{t+1} - A_{t+1}\hat{x}_{t+1|t})^T | y_{1:t}] \\ &= E[(A_{t+1}x_{t+1}-A_{t+1}\hat{x}_{t+1|t})(A_{t+1}x_{t+1}-A_{t+1}\hat{x}_{t+1|t})^T|y_{1:t}] + E[v_{t+1} v_{t+1} | y_{1:t}] \\ &= \mathbf{\color{darkred}{A^T_{t+1} P_{t+1|t} A^T_{t+1} + R}} \end{align*}
$$
[2]. calcualte the $Cov(y_{t+1},x_{t+1}|y_{1:t})$
$$
\begin{align*}
\mathbf{\color{darkred}{Cov(y_{t+1}, x_{t+1}|y_{1:t})}} &= E[(y_{t+1}-\hat{y}_{t+1|t})(x_{t+1} - \hat{x}_{t+1|t})|y_{1:t}] \\ &= E[(A_{t+1}x_{t+1} + v_{t+1} - A_{t+1}\hat{x}_{t+1|t})(x_{t+1} - \hat{x}_{t+1|t})^T|y_{1:t}] \\ &= A_{t+1} E[(x_{t+1} - \hat{x}_{t+1|t})(x_{t+1} - \hat{x}_{t+1|t})^T | y_{1:t}] \\ &= \mathbf{\color{darkred}{A_{t+1}P_{t+1|t}}}
\end{align*}
$$
[3]. calculate joint distribution
$$
\begin{bmatrix}
x_{t+1} \\
y_{t+1}
\end{bmatrix}
\sim N\begin{pmatrix}
\begin{bmatrix}
\hat{x}_{t+1|t} \\
A_{t+1} \hat{x}_{t+1|t} + \Gamma u_{t+1}
\end{bmatrix},
\begin{bmatrix}
\Phi P_{t|t} \Phi^T + Q & P_{t+1|t} A_{t+1}^T \\
A_{t+1} P_{t+1|t} & A^T_t P_{t+1|t} A^T_t + R
\end{bmatrix}
\end{pmatrix} \tag{3}
$$
▷ Second step: calculate the conditional distribution of $x_{t+1}|y_{t+1}$
정규분포의 결합 분포(joint distribution)에서 조건부 분포(conditional distribution)로 변환하는 공식을 이용합니다.
※ 다변수 정규분포 참고자료 → 식 (8.6.22)와 식 (8.6.25) 참고
[1]. conditional mean of $x_{t+1}|y_{t+1}$
$$
E[x_{t+1}|y_{t+1}] = \hat{x}_{t+1|t} + P_{t+1|t}A^T_{t+1}(A^T_t P_{t+1|t} A^T_t + R )^{-1}(y_{t+1} - A_{t+1} \hat{x}_{t+1|t} + \Gamma u_{t+1})
$$
[2]. conditional covariance of $x_{t+1}|y_{t+1}$
$$
Cov(x_{t+1},x_{t+1}|y_{t+1})= \Phi P_{t+1|t} \Phi^T + Q - P_{t+1|t} A_{t+1}^T(A^T_t P_{t+1|t} A^T_t + R )^{-1}A_{t+1} P_{t+1|t}
$$
[3]. conditional distribution
$$
x_{t+1}|y_{t+1} \sim N(\hat{x}_{t+1|t+1}, P_{t+1|t+1})\tag{4}
$$
- $\hat{x}_{t+1|t+1} = \hat{x}_{t+1|t} + P_{t+1|t}A^T_{t+1}(A^T_t P_{t+1|t} A^T_t + R )^{-1}(y_{t+1} - A_{t+1} \hat{x}_{t+1|t} + \Gamma u_{t+1})$
- $P_{t+1|t+1} = \Phi P_{t+1|t} \Phi^T + Q - P_{t+1|t} A_{t+1}^T(A^T_t P_{t+1|t} A^T_t + R )^{-1}A_{t+1} P_{t+1|t}$
우리가 Kalman filter를 통해 최종적으로 구하고자 했던 $x_{t+1}|y_{t+1}$의 분포를 구하였습니다.
▶ Algorithms of Kalman Filter
Kalman Filter의 알고리즘을 요약하면 다음과 같습니다.
🔶 Algorithm of Kalmann Filter
1. Initialize with $\hat{x}_{0|-1} = \mu_0, P_{0|-1} = \Sigma_0$
2. Time update
$$
\hat{x}_{t+1|t} = \Phi \hat{x}_{t|t} + \gamma u_t
$$
$$
P_{t+1|t} = \Phi P_{t|t} \Phi^T + Q
$$
3. Measurement Update
$$
E[x_{t+1}|y_{t+1}] = \hat{x}_{t+1|t} + P_{t+1|t}A^T_{t+1}(A^T_t P_{t+1|t} A^T_t + R )^{-1}(y_{t+1} - A_{t+1} \hat{x}_{t+1|t} + \Gamma u_{t+1})
$$
$$
Cov(x_{t+1},x_{t+1}|y_{t+1})= \Phi P_{t+1|t} \Phi^T + Q - P_{t+1|t} A_{t+1}^T(A^T_t P_{t+1|t} A^T_t + R )^{-1}A_{t+1} P_{t+1|t}
$$
[참고]
🔶 Kalman Gain Matrix
$$K_{t+1} = P_{t+1|t}A^T_{t+1}(A^T_t P_{t+1|t} A^T_t + R )^{-1}$$
$K_{t+1}$을 Kalman Gain Matrix라고 불리우며 Sherman-Morrison-Woodbury 이론에 따라서 다음과 같이 $K_{t+1}$을 표현할 수 있습니다.
$$
K_{t+1} = (P^{-1}_{t+1|t} + A^T_{t+1}RA_{t+1})^{-1} A^T_{t+1} R^{-1}
$$
2.2 (Rausch - Tung - Streibel) Smoothing
▶Define problem
$$ \text{Given, } x_{t+1}|y_{1:T}, \text{calculate distribution of } x_{t}|y_{1:T} , \, t<T$$
$$x_{t}|y_{1:T} \sim N(?,?)$$
▶Two property
(a). $x_t \perp y_{t+1|T} |x_{t+1}$
(b). (a)번의 성질에 의해, $p(x_t|x_{t+1},y_{1:T}) = p(x_t|x_{t+1},y_{1:t})$이 성립합니다.
▶ Calculate distribution of $x_t|y_{1:T}$
크게 3단계로 이루어집니다.
- calculate the joint distribution of $x_{t}, x_{t+1}|y_{1:t}( = x_{t}, x_{t+1}|y_{1:T})$
- calcualte the conditional distribution of $x_t|x_{t+1},y_{1:t}(= x_t|x_{t+1},y_{1:T})$
- calculate the $x_t|y_{1:T}$ using below two property
- (Tower property) $E[Z|X] = E[E[Z|Y,X]|X] \tag{5}$
- (Law of Total Conditional Variance) $Cov[Z|X] = Cov[E[Z|Y,X]|X] + E[Cov[Z|Y,X]|X] \tag{6}$
▷ First step: calculate the joint distribution of $x_{t}, x_{t+1}|y_{1:t}( = x_{t}, x_{t+1}|y_{1:T})$
우리가 계산해야 하는 값은 다음과 같습니다.
- $E[x_t|y_{1:t}] = \hat{x}_{t|t} , Cov(x_t,x_t|y_{1:t}) = P_{t|t}$ → known value($\because \text{definition of } (a), (b)$)
- $E[x_t+1|y_{1:t}] = \hat{x}_{t+1|t}, Cov(x_{t+1},x_{t+1}|y_{1:t}) = P_{t+1|t}$ → known value
- $Cov(x_t,x_{t+1}|y_{1:t})$ → unknown value
[1]. Calculate the $Cov(x_t,x_{t+1}|y_{1:t})$
$$\begin{align*}
\mathbf{\color{darkred}{Cov(x_t,x_{t+1}|y_{1:t})}} &= E[(x_t - \hat{x}_{t|t})(x_{t+1} - \hat{x}_{t+1|t})^T|y_{1:t}] \\ &= E[(x_t - \hat{x}_{t|t})(\Phi x_t + w_t - \Phi \hat{x}_{t|t})^T|y_{1:t}] \\ &= \mathbf{\color{darkred}{P_{t|t}\Phi^T}}
\end{align*}$$
[2]. Calculate joint distribution
$$x_{t},x_{t+1}|y_t \sim N(\begin{bmatrix} \hat{x}_{t|t} \\ \hat{x}_{t+1|t} \end{bmatrix}, \begin{bmatrix} P_{t|t} & P_{t|t} \Phi^T \\ \Phi P_{t|t} & P_{t+1|t}\end{bmatrix})$$
▷ Second step: calculate the conditional distribution of $x_t|x_{t+1},y_{1:t}(= x_t|x_{t+1},y_{1:T})$
[1]. calculate the conditional mean $x_t|x_{t+1},y_{1:t}$
$$E(x_t|x_{t+1},y_{1:T}) = E(x_t|x_{t+1},y_{1:t}) = \hat{x}_{t|t} + L_t(x_{t+1} - \hat{x}_{t+1|t})$$
- $L_t = P_{t|t}\Phi^TP^{-1}_{t+1|t}$
[2]. calculate the conditional covariance $x_t|x_{t+1},y_{1:t}$
$$Cov(x_t|x_{t+1},y_{1:T}) = Cov(x_t|x_{t+1},y_{1:t}) = P_{t|t} - L_tP_{t+1|t}L_t^T$$
[3]. calculate conditional distribution
$$x_t|x_{t+1},y_{1:t} \sim N(\hat{x}_{t|t} + L_t(x_{t+1} - \hat{x}_{t+1|t}), P_{t|t} - L_tP_{t+1|t}L_t^T)$$
▷ Third step: calculate the conditional distribution of $ x_t|y_{1:T} $
- "Tower property"(식 $(5)$)와 " Law of Total Conditional Variance "(식 $(6)$)을 이용하여 조건부 평균과 조건부 공분산을 구합니다.
[1]. calculate the conditional mean $x_t|y_{1:T}$
$$\begin{align*}
\mathbf{\color{darkred}{\hat{x}_{t|T}}} &= E[x_t|y_{1:T}] \\ &= E[E[x_t|x_{t+1}, y_{1:T}]|y_{1:T}] \\ &= E[\hat{x}_{t|t} + L_t(x_{t+1} - \hat{x}_{t+1|t})|y_{1:T}] \\ &= \mathbf{\color{darkred}{\hat{x}_{t|t} + L_t(\hat{x}_{t+1|T} - \hat{x}_{t+1|t})}}
\end{align*}$$
[2]. calculate the conditional covariance $x_t|y_{1:T}$
$$\begin{align*}
\mathbf{\color{darkred}{P_{t|T}}} &= Cov[x_t|y_{1:T}] \\ &= Cov(E[x_t|x_{t+1}, y_{1:T}]|y_{1:T}) + E[Cov[x_t|x_{t+1},y_{1:T}]|y_{1:T}] \\ &= Cov[\hat{x}_{t|t} + L_t(x_{t+1} - \hat{x}_{t+1|t})|y_{1:T}] + E[P_{t|t} - L_tP_{t+1|t}L
^T_{t}|y_{1:T}] \\ &= L_tP_{t+1|t}L^T_t + P_{t|t} - L_tP_{t+1|t}L^T_t \\ &= \mathbf{\color{darkred}{P_{t|t} + L_t(P_{t+1|T} - P_{t+1|t})L^T_t}}
\end{align*}$$
[3].conditional distribution
$$x_t|y_{1:T} \sim N(\hat{x}_{t|T}, P_{t|T})$$
- $\hat{x}_{t|T} =\hat{x}_{t|t} + L_t(\hat{x}_{t+1|T} - \hat{x}_{t+1|t}) $
- $P_{t|T}=P_{t|t} + L_t(P_{t+1|T} - P_{t+1|t})L^T_t$
▶Algorithm of (Rausch - Tung - Streibel) Smoothing
(Rausch - Tung - Streibel) Smoothing의 알고리즘을 요약하면 다음과 같습니다.
🔶 Algorithm of (Rausch - Tung - Streibel) Smoothing
[1]. 먼저, Kalman Filter를 통해 filtered와 one-step prediciton quantities인 $\hat{z}_{t|t},\,\hat{z}_{t+1|t}, P_{t|t}, P_{t+1|t}$을 얻습니다($0,1,\cdots,T$).
- filtered quantities : $\hat{z}_{t|t}, P_{t|t}$
- one-step prediction quantities: $\hat{z}_{t+1|t}, P_{t+1|t}$
[2]. $\hat{x}_{T|T}, P_{T|T}$으로 smoother 초기화
[3]. $p(x_{t+1}|y_{1:T})$가 주어진 상황에서, $p(x_t|y_{1:T})$
본 글에서는 observation data $y_{1:s} = \{y_1, \cdots, y_s\}$가 주어졌을 때, hidden state $x_t$를 추정하는 (Gaussian) State Space Model에 대해 알아보았습니다.
'Time Series Analaysis > Time Series Analysis' 카테고리의 다른 글
| Convolutional LSTM network(ConvLSTM) (0) | 2024.01.29 |
|---|---|
| Gated Recurrent Unit(GRU) (2) | 2024.01.23 |
| Long Short Term Memory(LSTM) (0) | 2024.01.22 |
| Recurrent Neural Network(RNN) (0) | 2024.01.22 |



