본 글에서는 Convolution Layer에서 합성곱 연산이 어떻게 이루어지는지에 대해 정리한 글입니다.
▼ Contents
1. Convolution v.s. Cross correlation
2. Convolution Layer가 필요한(사용하는) 이유
3. Convolution Layer 계산 방법
1. Convolution v.s. Cross correlation
▶ Convolution
$$(f * g)(t) = \int^{\infty}_{-\infty} f(\tau) g(t-\tau)d\tau$$
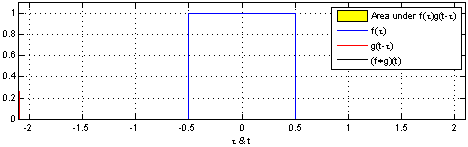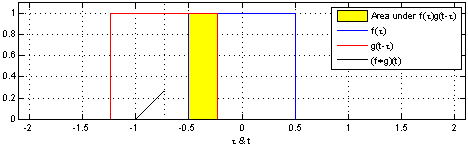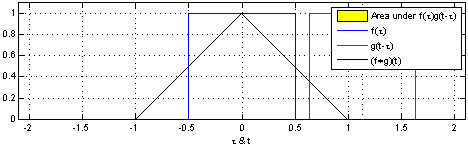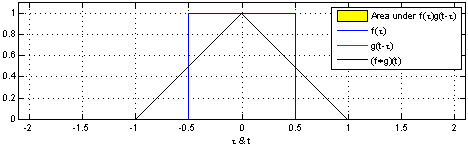

(1). 함수 $\color{blue}{f(\tau)}$와 또 다른 함수 $\color{red}{g(\tau)}$가 존재한다고 가정하겠습니다.
(2). 함수 $\color{red}{g(\tau)}$를 $y$축을 기준으로 좌우 반전(reverse) 후 t만큼 이동(shift)합니다. → $\color{red}{g(-\tau)}$ → $\color{red}{g(t-\tau)}$
(3). $\color{blue}{f(\tau)}$와 $\color{red}{g(t-\tau)}$의 겹치는 구간을 계산합니다. → $(f * g)(t) = \int^{\infty}_{-\infty} \color{blue}{f(\tau)} \color{red}{g(t-\tau)} d\tau$
※ 두 함수 $f$, $g$의 합성곱 연산은 수학 기호로 $*$로 표시합니다.
[Figure 1]은 $t$를 $(-\infty, \infty)$만큼 이동함에 따라 $f$와 $g$의 합성곱의 연산 결과(검은색 선)를 보여주는 그림입니다.
▶ Cross Correlation
$$(f * g)(t) = \int^{\infty}_{-\infty} f(\tau) g(t + \tau)$$
Cross correlation은 $y$ 축을 기준으로 좌우 반전을 하지 않는다는 점을 제외하면 convolution과 연산 과정은 같습니다.

(1). 함수 $\color{blue}{f(\tau)}$와 또 다른 함수 $\color{red}{g(\tau)}$가 존재한다고 가정하겠습니다.
(2). 함수 $\color{red}{g(\tau)}$를 t만큼 이동(shift)합니다. → $\color{red}{g(t+\tau)}$
(3). $\color{blue}{f(\tau)}$와 $\color{red}{g(t-\tau)}$의 겹치는 구간을 계산합니다. → $(f * g)(t) = \int^{\infty}_{-\infty} \color{blue}{f(\tau)} \color{red}{g(t+\tau)} d\tau$
앞으로 살펴볼 Convolution Layer에서 합성곱(convolution) 연산은 정확하게는 cross correlation이며
함수 $f$는 입력 이미지, 함수 $g$는 kernel(filter, window), $(f * g)(t)$는 feature map(activation map)입니다.
하나의 kernel(filter, sliding window) $g$에 대해 입력 이미지 $f$를 쭉 지나면서 이미지의 특정 부분들이 필터와 얼마나 유사한지를 계산합니다.

※ [Figure 3]에서 묘사된 PSF는 Point Spread Function으로 말 그대로 점을 퍼뜨리는 기능을 수행합니다. PSF는 kernel(or filter, sliding window)를 지칭한다고 생각하시면 될 것 같습니다.
용어에 대한 설명 및 convolution layer에서의 합성곱 연산에 대한 내용은 [Section 3: Convolution Layer]에서 살펴보겠습니다.
▶ Convolution $*$의 특성
- Commulative(교환 법칙): $a*b = b*a$
- Associative(결합 법칙): $a*(b*c) = (a*b)*c$
- Distributes over addition(덧셈에 대한 분배법칙): $a*(b+c) = a*b + a*c$
- Scalars Factor Out(상수 꺼내기): $k(a*b) = a * kb = k(a*b)$
- Identity vector(고유 벡터): $e=[0,0,1,0,0] \to a*e=a$
2. Convolution Layer의 필요성
Input data에 따른 output value를 산출할 때 보통 다음과 같은 과정을 통해 모델은 가중치(weight)를 학습합니다.
[Process: Input → Feature Extractor → Trainable Classifier → Output]
Feature Extractor에서는 input data에 대한 특성을 추출합니다. 추출된 특성을 바탕으로 Trainable Classifier에서는 최종 output value를 산출하며 보통 full connected multi-layer network를 사용합니다. Feature Extractor에서도 full connected multi-layer network를 사용할 경우 효과적이기는 하지만 다음과 같은 문제점이 존재합니다.
(Problem 1). 메모리 요구량
수 백만개의 픽셀(변수)로 이루어진 이미지 데이터의 경우 많은 매개변수(parameter, weight)를 필요로 합니다. 학습해야 하는 매개변수가 많을수록 필요로 하는 데이터의 양도 커지며 결국 큰 메모리가 요구됩니다.
(Problem 2). 왜곡(distortion), 이동(shift), 크기(scale)
Input data의 약간의 왜곡 혹은 이동만 취해져도 다른 데이터로 인식합니다.
(Problem 3). Topology 무시
이미지의 경우 인접한 픽셀(pixel) 간에는 상당히 깊은 연관성이 존재합니다. 하지만, fully connected layer의 경우는 이와 같은 공간적인 특성(local correlation)을 무시합니다.
Convolution layer에서는 위의 3가지 문제점을 "Local Connection", "Weight Sharing", "Sub-sampling(or Pooling)"을 사용하여 보완합니다.
3. Convolution Layer
▶ 이미지 정형화
Convolution Layer에 대해 본격적으로 설명하기에 앞서 이미지 데이터를 정형화하는 방법에 대해 살펴보겠습니다. 정형 데이터화란, 컴퓨터로 식별 가능한 형태로 데이터를 변화하는 것을 의미합니다. 이미지는 픽셀(pixel) 단위로 구성되어 있고 각 픽셀은 RGB(Red, Green, Blue) 값으로 구성되어 있습니다.
흑백 이미지는 $W \times H \times 1$, 컬러 이미지는 $W \times H \times 3$의 배열(혹은 행렬)로 표현 할 수 있습니다. 마지막 $3$은 각각 Red, Green, Blue의 강도의 값으로 구성할 수 있으며 마지막 차원은 channel이라고 지칭합니다.

3.1 Filter(Kernel, Silding Window)

Convolution Layer의 경우, input data로 전체 데이터가 아닌 일부분만 입력으로 받습니다.
[Figure 4]와 같이 $3 \times 3$ filter(or kernel)를 한 칸씩 이동해 가면서(stride = 1)
가중치 $W$와 입력값 $X$을 곱한 값에 활성화 함수를 취하여 hidden layer(은닉층)으로 넘겨줍니다.
- Input Data: $X = \begin{pmatrix} x_1 & x_2 & x_3 \\ x_4 & x_5 & x_6 \\ x_7 & x_8 & x_9 \end{pmatrix}$, Filter or Weight : $W = \begin{pmatrix} w_1 & w_2 & w_3 \\ w_4 & w_5 & w_6 \\ w_7 & w_8 & w_9 \end{pmatrix}$
[예시]
<< (1). 빨간색 박스 연산 과정: 입력 이미지에서 빨간 박스에 해당하는 부분과 필터(혹은 커널)은 얼마나 유사한가?>>
- Input Data $X = \begin{pmatrix} -1 & -1 & -1 \\ -1 & 1 & -1 \\ -1 & -1 & 1 \end{pmatrix}$, Filter(Weight) $W = \begin{pmatrix} 1 & -1 & -1 \\ -1 & 1 & -1 \\ -1 & -1 & 1 \end{pmatrix}$ → $ X * W = 0.77$
※ $\scriptsize 0.77 = ((-1 \times 1) + (-1 \times -1) + (-1 \times -1) + (-1 \times -1) + (1 \times 1) + (-1 \times -1) + (-1 \times -1) + (-1 \times -1) + (1 \times 1))/9$
<< (2). 초록색 박스 연산 과정: 입력 이미지에서 초록색 박스에 해당하는 부분과 필터(혹은 커널)은 얼마나 유사한가? >>
- Input Data $X = \begin{pmatrix} -1 & -1 & -1 \\ 1 & -1 & -1 \\ -1 & 1 & 1 \end{pmatrix}$, Filter(Weight) $W = \begin{pmatrix} 1 & -1 & -1 \\ -1 & 1 & -1 \\ -1 & -1 & 1 \end{pmatrix}$ → $ X * W = -0.11$
※ $\scriptsize -0.11 = ((-1 \times 1) + (-1 \times -1) + (-1 \times -1) + (1 \times -1) + (-1 \times 1) + (-1 \times -1) + (-1 \times -1) + (-1 \times 1) + (-1 \times 1))/9$
[예시] 및 [Figure 4], [Figure 5]를 통해 알 수 있듯이 Filter(kernel, window)의 값 $w_0, w_1, \cdots, w_9$에 따라 산출되는 값이 다르다는 것을 짐작하실 수 있습니다.

▶ Convolution Layer의 중요한 특성 (1)
- Full Connected Layer의 경우, 입력 데이터의 차원만큼의 가중치가 필요합니다.
- Convolution Layer의 경우, 커널(혹은 필터)의 크기만큼만 필요합니다.
[Figure 4]를 통해 예시를 들면,
Full connection layer를 통해 가중치 학습을 진행하면, $81$개의 가중치가 필요한 반면 convolution layer를 통해 가중치 학습을 진행한 경우 $9$개의 가중치만 필요합니다.
즉, 요구되는 메모리 양이 현저히 감소한 것을 확인할 수 있습니다. 그리고 입력값 $X$와 가중치 $F$(or $W$)의 convolution 결과값을 feature map 혹은 activation map이라고 지칭합니다.
3.2 Feature map or Activation map
Feature map은 필터(혹은 커널) 하나당 입력 이미지 전체에 대한 필터(혹은 커널)의 일치 정도를 나타내는 행렬입니다.
하나의 이미지에 대하여 여러 개의 필터(혹은 커널) 를 적용할 수 있으며 필터(혹은 커널) 하나당 입력 이미지 전체에 대한 필터(혹은 커널) 의 일치 정도를 산출합니다. 예를 들어서, 하나의 이미지에 필터(혹은 커널)을 3개 사용한다면 feature map도 역시 3개가 생성됩니다.

Feature map $O$의 size는 입력 이미지와 필터(혹은 커널)의 크기, stride의 크기에 따라 결정됩니다.
$$ O = \text{floor}(\dfrac{I-K}{S} + 1)$$
- $O$: feature map의 size
- $I$: Input data의 size
- $K$: filter의 size
- $S$: stride의 size
3.3 Stride
Stride(스트라이드)란, 필터(혹은 커널)을 입력 이미지 혹은 feature map에 적용할 때 움직이는 간격을 지칭합니다.
- Stride를 $1$로 설정한 경우는 필터(혹은 커널)이 한 칸씩 이동하며 모든 pixel에 대해 연산을 수행합니다.
- Stride를 $2$로 설정한 경우는 필터(혹은 커널)이 두 칸씩 이동하며 모든 pixel에 대해 연산을 수행하지 않고 듬성듬성 수행합니다.
Stride는 주로 size를 줄이고 싶을 때 사용합니다. Stride의 크기를 키울수록 산출되는 feature map의 크기는 작아집니다.
[예시]

- Stride가 $1$인 경우 필터(혹은 커널)이 한 칸씩 이동한 것을 확인할 수 있으며
산출된 feature map의 크기는 $\dfrac{7-3}{1} + 1 = 5$인 것을 확인할 수 있습니다. - Stride가 $2$인 경우 필터(혹은 커널)이 두 칸씩 이동한 것을 확인할 수 있으며
산출된 feature map의 크기는 $\dfrac{7-3}{2} + 1 = 3$인 것을 확인할 수 있습니다.
3.4 Padding
반대로 이미지 주변에 특정 값으로 채워넣는 padding(패딩)은 size가 줄어드는 것을 방지해주는 역할을 합니다.
[Padding의 사용 목적: 입력 데이터에 대한 충분한 특성을 뽑아내기 위해서]
[1]. 반복적으로 합성곱 연산을 적용하였을 때 feature map의 크기가 작아지는 것을 방지하여 충분한 특성을 뽑아낼 수 있습니다.
[2]. 이미지의 모서리 부분의 정보 손실을 방지할 수 있습니다.
[예시]

- 좌상단부터 필터(혹은 커널)을 끝까지 이동시켰을 때, 각 픽셀(pixel)이 이용된 횟수를 체크한 그림입니다.
- 이미지의 중심부는 $4$회로 충분히 사용된 반면,
모서리 부분의 픽셀(pixel)들은 상대적으로 이용횟수가 적은 것을 확인할 수 있습니다. - Padding을 사용해줌으로써 이미지의 모든 부분이 중심부처럼 합성곱 연산에 반영되어 정보 손실을 줄일 수 있습니다.
Padding까지 적용한 경우, 산출되는 feature map의 size는 다음과 같습니다.
$$ O = \text{floor}(\dfrac{I-K+2P}{S}+1)$$
- $I$: 입력 데이터의 크기
- $K$: 필터(혹은 커널)의 크기
- $P$: padding의 크기
- $S$: stride의 크기
3.5 Sub-sampling or Pooling
Sub-sampling(Down sampling)은 현재 pooling이라는 용어로 주로 사용되며 데이터의 공간적인 특성을 유지하면서 크기를 줄여주는 층으로 연속적인 convolution layer 사이에 주기적으로 넣어줍니다.
▶ Convolution Layer의 중요한 특성 (2)
▶ Pooling의 특징: 데이터의 공간적인 특성을 그대로 유지하면서 크기를 줄여, 특정위치에서 큰 역할을 하는 특징을 추출하거나(→ max pooling) 전체를 대변하는 특징( → Average pooling )을 추출할 수 있습니다.
[1]. Max Pooling
- Pooling filter 영역에서 가장 큰 값만을 전달하고 다른 정보는 버리는 방법입니다.
- 자극의 관점에서 보면, max pooling은 가장 강한 자극만 남기고 나머지는 무시합니다.
- 합성곱 연산 관점에서 보면, max pooling은 pooling filter 내에서 필터(혹은 커널, 가중치)의 모양과 가장 비슷한 부분을 전달합니다.
[2]. Average Pooling
- Pooling filter 영역에 있는 값들의 평균을 전달하는 방법입니다.
- 자극의 관점에서 보면, average pooling은 평균적인 자극을 전달합니다.
- 합성곱 연산 관점에서 보면, average pooling은 pooling filter 내에서 필터(혹은 커널, 가중치)의 모양과 평균적으로 얼마나 일치하는지를 뽑아냅니다.
[예시]

$4 \times 4$의 feature map에 대해서 $2 \times 2$의 pooling filter을 적용한 예시입니다(stride=2로 설정).
4가지의 영역 중 초록색 영역과 하늘색 영역에 대해서만 살펴보겠습니다.
<< 초록색 영역 >>
- Max Pooling: 가장 큰 값인 $32$만을 전달하고 나머지는 버립니다.
- Average Pooling: 평균값인 $\dfrac{32 + 10 + 4 + 14}{4} = 15$를 전달합니다.
<< 보라색 영역 >>
- Max Pooling: 가장 큰 값인 $19$만을 전달하고 나머지는 버립니다.
- Average Pooling: 평균값인 $\dfrac{11 + 17 + 9 + 19}{4} = 14$를 전달합니다.
<< 주황색 영역 >>
- Max Pooling: 가장 큰 값인 $20$만을 전달하고 나머지는 버립니다.
- Average Pooling: 평균값인 $\dfrac{20 + 4 + 8 + 12}{4} = 11$을 전달합니다.
<< 하늘색 영역 >>
- Max Pooling: 가장 큰 값인 $27$만을 전달하고 나머지는 버립니다.
- Average Pooling: 평균값인 $\dfrac{16 + 27 + 7 + 14}{4} = 16$을 전달합니다.
Average Pooling보다 Max Pooling이 더 좋다고 알려져 있어 보통 Max Pooling을 많이 사용합니다.
3.6 Local Connectivity & Weight Sharing
Convolution Layer는 global connectivity가 아닌 local connectivity라는 점과 하나의 이미지에 같은 커널(혹은 필터)를 stride 크기만큼 이동해 가면서 적용함으로써 weight sharing(가중치 공유)를 한다는 중요한 특성이 존재합니다.
▶ Convolution Layer의 중요한 특성 (3)
Local Connectivity and Weight Sharing




Convolution layer의 경우 같은 커널(혹은 필터)에 대해서(→ weight sharing)
각 커널마다 모든 pixel에 대해서 connect 되어 있지 않고( → global connectivity)
일부 pixel에 대해서만 connect 되어 있는 것을 확인할 수 있습니다(-> local connectivity).
[Figure 10]은 $9 \times 9$ 이미지에 동일한 $2 \times 2$ 필터(혹은 커널)을 적용함으로써 stride 크기만큼 이동해 가면서 feature map을 생성하는 과정이 담겨져 있습니다.

인공신경망 그림으로 표현하면 [Figure 11]과 같습니다.
- Input Data: $3 \times 3$ 2D image
- Hidden layer의 차원: $4$
- (a).Fully Connected Layer로 총 12개의 weight가 필요합니다.($W \in \mathbb{R}^{3 \times 4}$)
- (b). Convolution Layer로 총 $3 \times 3$ image에 $2 \time 2$ 커널(혹은 필터)를 적용함으로써 총 4개의 weight만 필요합니다.
이처럼 Convolution layer는 각 이미지에 동일한 커널(혹은 필터)를 stride 크기만큼 이동해 local하게 적용함으로써 trainable parameters(weight)의 수가 현저히 감소하는 것을 알 수 있습니다.
3.7 Multiple Input Channel or Multiple Output Channel
지금까지는 흑백 이미지에 대해 살펴보았다면 [Section 3.7]에서는 컬러 이미지에 대해 살펴보겠습니다.
[1]. Multiple Input Channel(Input Channel)
컬러 이미지는 흑백 이미지와는 다르게 channel 수가 $3$개 이며 RGB 각각에 다른 가중치로 convolution(→ 커널(혹은 필터)의 channel이 $1$이 아닌 $3$)을 하고 결과를 더해줍니다.
※ 주의할 점: 커널(혹은 필터) 채널이 $3$이라고 해서 커널(혹은 필터)의 개수가 $3$이라는 것을 의미하지 않습니다.

(1). [Figure 11]은 Input channel $2$인 경우로 커널(혹은 필터)의 channel도 $2$인 것을 확인할 수 있습니다.
(2). 각의 channel에 다른 가중치로 convolution을 하고 두 개의 결과를 합치는 과정을 확인할 수 있습니다.
(3). 커널(혹은 필터)의 개수는 $1$개임도 확인할 수 있습니다.
- 항상 입력 데이터에 대한 채널의 수와 커널의 채널 수는 일치해야 합니다.
[2]. Multiple Output Channel(Output Channel)
커널(혹은 필터)의 개수를 $1$개가 아닌 $2$개 이상으로 설정한 경우는 output인 feature map의 채널이 됩니다.

[Figure 12]는 입력 데이터의 채널이 $3$, 커널(혹은 필터)의 개수를 $2$개로 설정한 경우입니다.
- 입력 데이터의 채널이 $3$이므로 커널(혹은 필터)의 채널도 $3$으로 설정합니다.
- 커널(혹은 필터)의 개수가 $2$개 이므로 output인 feature map의 채널이 $2$인 것을 확인할 수 있습니다.
3.8 $1$D convolution v.s. $2$D convolution v.s. $3$D convolution
Convolution(합성곱)은 입력 데이터의 차원의 수가 아닌 이동 방향의 수에 따라 $1$D, $2$D, $3$D로 구분합니다.



- $1$D convolution은 이동 방향이 한 개입니다(x축).
- $2$D convolution은 이동 방향이 두 개입니다(x축, y축).
- $3$D convolution은 이동 방향이 세 개입니다(x축, y축, z축).
3.9 Convolution Neural Network의 구조
마지막으로 전형적인 Convolution Neural Network(CNN)의 구조를 살펴보겠습니다.

[Feature Learning(Feature Extractor)]
입력값(Input Image)에 대해 몇 번의 합성곱 연산을 활성화 함수와 함께 적용한 이후(Convolution + Non-linearity)
풀링(pooling)을 통해 전체 크기를 줄여주는 과정을 반복합니다.
[Classification]
Feature Learning에서 convolution layer을 활용해 특성을 충분히 추출한 후에는
추출된 특성들을 바탕으로 flattening layer을 통해 각 클래스별 확률을 산출하거나(→ classification problem)
특정 수치들을 산출합니다(→ regression problem).
※ 참고: Flattening Layer
Flattening Layer는 convolution layer 및 pooling layer에서 추출한 feature 를 output layer( → fully connected layer)에 연결하여 결과값을 산출하기 위해 필요한 layer입니다.
본 글에서는 convolution layer에서 합성곱 연산이 어떻게 이루어지는지 및 중요한 특성들에 대해 정리하였습니다.
다음 글에서는 Convolution Neural Network(CNN)을 발표하였던 Yann Lecun 연구팀에서 1998년에 개발한 CNN 알고리즘인 LeNet-5 구조에 대해 살펴보고자 합니다.
■ 참고자료
3. Deep Learning: Basics and Convolution Neural Networks(CNNs)
'Deep Learning > Convolution Neural Network' 카테고리의 다른 글
| Semantic Segmentation (1): Sliding Window (0) | 2024.03.20 |
|---|---|
| Computer Vision Task 개요 (0) | 2024.03.20 |
| LeNet-5 (0) | 2024.03.19 |


