본 글은 Self-Supervised Learning(SSL) 방법론 중 contrastive learning 기법 중 하나인 Boostrap Your Own Latent(BYOL)에 대해 설명하겠습니다.
논문 "Boostrap Your Own Latent: A new approach to Self-Supervised Learning"을 참고하여 작성하였습니다.
Computer Vision(CV)에서 데이터를 가장 잘 표현하는 representation vector를 학습하는 것은 가장 중요한 태스크 중 하나입니다.
▶ Self-Supervised Learning(SSL): Constrastive Learning
Self-supervised Learning은 representation learning의 일종으로 unlabeled dataset으로부터 좋은 data representation을 얻는 것을 목표로 합니다. SSL 방법론 중 contrastive learning은 임베딩 공간(embedding space) 상에서 비슷한 속성을 가진 객체(positive pairs)끼리는 서로 가깝게, 다른 속성을 가진 객체(negative pairs)끼리는 서로 멀리 위치하도록 학습합니다.
- Self-Supervised Learning(SSL)에 대한 참고자료: https://iy322.tistory.com/79
▶ Contrastive Learning의 종류: Inter-sample classification / Feature Clustering / Non-contrastive Learning
Inter-sample classification과 Feature Clustering은 positive pairs간의 거리는 가깝게 negative pairs간의 거리는 멀게 학습함으로써 collasped problem을 방지합니다.
※ collasped problem: 어떤 객체가 입력되도 동일한 representation vector(constant vector)가 출력되는 현상
하지만, negative sample이 사용되기 때문에 큰 배치 사이즈가 필요하여 메모리 비용이 크며 어떤 data augmentation 방법을 사용하는가에 따라 성능이 달라진다는 단점이 존재합니다.
이와 같은 단점을 보완한 방법이 본 글에서 다룰 Boostrap Your Own Latent(BYOL)입니다. BYOL은 negative sample이 필요없는 non-contrastive learning 방법론이며 우수한 성능을 보이는 것으로 알려져 있습니다. 또한, constrastive method보다 data augmentation에 로버스트합니다.
0. Boostratp Your Own Latent(BYOL)
Boostrap Your Own Latent(BYOL)은 2개의 뉴럴 네트워크("online network", "target network")가 사용되며 두 뉴럴 네트워크는 서로 상호작용하며 학습합니다.

▶ Process of BYOL
[1]. 타겟 이미지로부터 데이터를 증강합니다(data augmentation: random crop, rotation...).
[2]. 같은 이미지로부터 생성된(혹은 변형된) 서로 다른 두 개의 이미지는 각각 online network와 target network의 입력 데이터가 됩니다.
[3]. Online network은 target newtork의 output $z'_{\xi}$를 예측하도록 학습합니다.
[4]. Online network은 stochastic gradient 방법으로 파라미터가 업데이트 되는 반면, Target network은 online network의 파라미터를 사용하여 moving average 방법론을 통해 파라미터를 업데이트합니다.
보다 자세한 내용을 수식과 함께 [Section 1: Description on BYOL]에서 살펴보겠습니다.
1. Description of BYOL
▶ Goal of BYOL
BYOL은 downstream task에 사용될 representation vector $y_{\theta}$를 학습하는 것을 목표로 합니다.
BYOL은 앞서 말했듯이 online network와 target network를 사용하여 $y_{\theta}$를 산출합니다.
▶ Algorithm of BYOL

[1]. Data Augmentation
먼저, target data $x_i \in \mathbf{B}$에 서로 다른 두 개의 데이터 증강 기법($t \sim T, \, \, t' \sim T'$)을 적용하여 데이터 증강을 합니다( → $v = t({x_i})$, $v' = t'(x_i)$).
[2]. Output of Online Network and Target Network
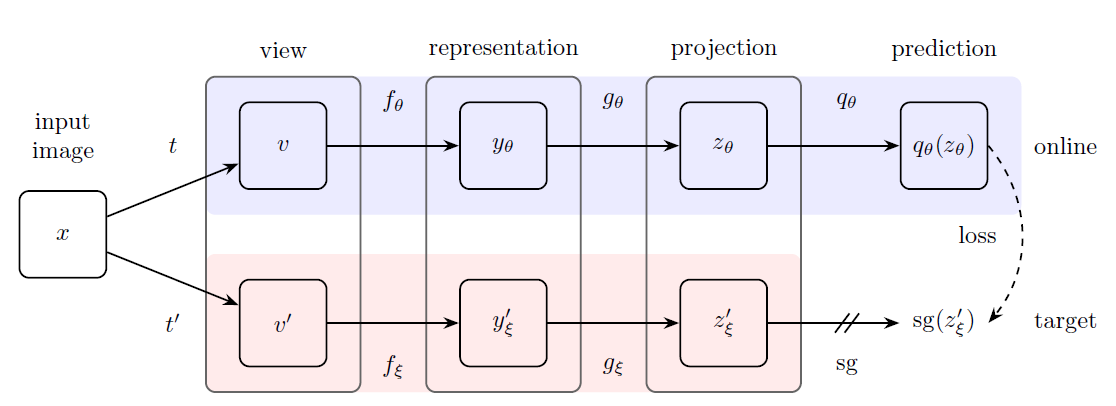
[2-1]. Process of Online Network
Online Network의 파라미터(가중치) 집합을 $\theta$로 정의하겠습니다.
Online Network는 크게 3단계로 구성되어 있습니다.
- encoder $f_{\theta}$
- projector $g_{\theta}$
- predictor $q_{\theta}$: 오직 online network에만 predictor function이 존재합니다.
Online Network의 입력값이 $v$인 경우, 산출값은 다음과 같습니다.
$$z_{\theta} \gets g_{\theta}(f_{\theta}(v))$$
$$\text{Projection: } q_{\theta}(z_{\theta}) \tag{1}$$
[2-2]. Process of Target Network
Target Network의 파라미터(가중치) 집합을 $\xi$로 정의하겠습니다.
Target Network는 크게 2단계로 구성되어 있습니다.
- encoder $f_{\xi}$
- projector $g_{\xi}$
Target Network의 입력값이 $v'$인 경우, 산출값은 다음과 같습니다.
$$z'_{\xi} \gets g_{\xi}(f_{\xi}(v')) \tag{2}$$
[2-3]. L2-normalization
$$\bar{q_{\theta}}(z_{\theta}) = q_{\theta}(z_{\theta})/||q_{\theta}(z_{\theta})||_2$$
$$\bar{z}'_{\epsilon} = z'_{\epsilon} / ||z_\epsilon '||_2$$
[2-4]. Mean Squared Error between the normalized predictions $\bar{q_{\theta}}(z_{\theta})$ and target projections $\bar{z}'_{\xi}$:
Online Network의 경우, target network의 산출값 $z'_{\xi}$를 예측하도록 학습하기 때문에
online network의 산출값인 $q_{\theta}(z_{\theta})$와 target network의 산출값인 $z'_{\xi}$의 유사도를 판단하도록 손실함수를 정의합니다.
$$L_{\theta, \xi} = || \bar{q_{\theta}}(z_{\theta}) - \bar{z}'_{\xi}||^2_2 = 2 - 2 \cdot \dfrac{<q_{\theta}(z_{\theta}), z'_{\xi} >}{||q_{\theta}(z_{\theta})||_2 \cdot ||z'_{\xi}||_2}$$
[2-1] ~ [2-4]를 이번에는 online network의 입력값이 $v'$인 경우, target network의 입력값이 $v$인 경우에 대해서 수행합니다.
$$\tilde{L}_{\theta,\xi} = || \bar{q_{\theta}}(z_{\theta}') - \bar{z}_{\xi}||^2_2 = 2 - 2 \cdot \dfrac{<q_{\theta}(z_{\theta}'), z_{\xi} >}{||q_{\theta}'(z_{\theta})||_2 \cdot ||z_{\xi}||_2}$$
[3]. Loss Function of BYOL
$$L^{\text{BYOL}}_{\theta, \xi} = L_{\theta, \xi} + \tilde{L}_{\theta,\xi} \approx -2 \cdot (\dfrac{<q_{\theta}(z_\theta), z'_{\xi}>}{||q_{\theta}(z_{\theta})||_2 \cdot || z_{\xi}||_2} + \dfrac{<q_{\theta}(z'_{\theta}), z_{\xi}>}{||q_{\theta}(z'_{\theta})||_2 \cdot ||z_{\xi}||_2})\tag{4}$$
[4]. Optimization
우리는 ""오직 $\theta$""에 대해서만 식 $(4)$가 최소화되록 stochastic gradient를 수행합니다. [Figure 1]과 [Figure 3]에서 묘사되었듯이 target network에는 "" stop gradient"가 존재합니다. Target network의 경우, $\theta$ 값들의 지수 이동 평균(exponential moving average)로 표현됩니다.
$$\text{ Update Online Parameters: } \theta \leftarrow \text{optimizer}(\theta, \nabla_{\theta}L^{\text{BYOL}}_{\theta,\xi},\eta)$$
$$\text{Update Target Parameters: } \xi \leftarrow \tau \xi + (1-\tau)\theta$$
- $\eta$: learning rate(학습률)
[5]. Output of BYOL
$$\text{encoder}: f_{\theta}$$
3. Key Point of BYOL
[Section 2: Description of BYOL]에서 BYOL의 구조와 학습 과정에 대해 살펴보았습니다.
마지막으로 [Section 3: Key Point of BYOL]에서 BYOL의 구조 특징을 바탕으로 negative sample이 없어도 collasped problem이 발생하지 않은 이유에 대해 살펴보겠습니다.
논문에서는 두 가지 이유로 collasepd problem이 발생하지 않는다고 주장합니다.
첫째, online network와 target network은 비대칭 구조로 online network에만 predictor function이 존재합니다.
둘째, online network의 파라미터의 지수 이동 평균을 target network의 파라미터 업데이트 방법으로 사용함으로써 online projection에 더 많은 정보를 인코딩하도록 장려합니다.
본 글에서는 Self Supervised Learning 중 Boostrap Your Own Latent(BYOL) 방법론에 대해 살펴보았습니다.
다음 글에서는 BYOL 방법론을 적용한 멀티 모달 추천시스템인 Boostrap Multi Modal Recommendation Model(BM3)에 대해 살펴보겠습니다.
'Deep Learning > Self Supervised Learning' 카테고리의 다른 글
| Self Supervise Learning(SSL) (0) | 2024.05.14 |
|---|
