본 글에서는 멀티 모달 추천시스템(multi modal recommendation system) 방법론 중 negative sample이 필요없는 Boostrapped Multi-Modal Model(BM3)에 대해 살펴보겠습니다.
또한, 본 글은 논문 'Boostrap Latent Representation for Multi-Modal Recommendation(2023)'을 바탕으로 작성하였음을 명시합니다.
▶ 멀티 모달 추천시스템(Multi-Modal Recommendation System)
멀티 모달 추천시스템이란, 사용자 로그 정보뿐만 아니라 이미지 혹은 텍스트 정보를 결합하여 사용자(user)와 상품(item)간의 상호작용(interaction)을 고려하여 사용자가 선호할 상위 상품을 제안하는 소프트웨어 도구이자 기술을 의미합니다.
멀티 모달 추천시스템의 대표적인 방법론으로는 "Multi-Modal Graph Convolution Neural Network(MMGCN, 2019)"과 "Graph Refined Convolution Network(GRCN) - 2020" , "LATTICE", "FREEDOM" 등이 존재합니다. Graph Convolution Network(GCN)을 활용하여 다양한 상호작용 그래프를 생성하고, 이를 통해 사용자와 상품의 representation vector를 학습합니다.
- "user-item interaction graph": 각 사용자와 상품간의 상호작용 모델링
- "user-user interaction graph": 사용자간의 상호작용 모델링
- "item-item interaction graph": 상품간의 관계 모델링
기존의 멀티 모달 추천시스템은 Bayesian Personalized Ranking(BPR) loss를 사용하였기 때문에 negative sample이 필요했습니다.
※ [참고자료] Bayesian Personalized Ranking(BPR)
하지만, 이는 large graph에 대해서 계산 비용이 크며 훈련 과정에서 noisy supervision signal이 발생할 수도 있습니다.
BM3는 이 문제점을 보완하고자 negative sample이 필요 없는 "Boostrap Your Own Latent(BM3)" 모델을 응용하였습니다. 또한, BM3는 GCN 대신 GCN에서 추천시스템의 성능을 저해하는 요소를 제거한 "Light GCN"을 사용하였습니다.
※ [참고자료] Boostrap Your Own Latent(BYOL)
▶ BM3 = BYOL + Light GCN
즉, BM3는 BYOL과 Light GCN을 결합한 모델입니다. 다만, BM3의 경우, BYOL에서 target network를 제거하고 dropout mechanism을 사용함으로써 BYOL 모델 구조보다 더 단순한 형태로 만들었고 이는 모델 파라미터 개수의 감소 효과를 가져다 주었습니다.
▶ Loss function of BM3 = Multi-Modal Contrastive Loss
또한, BM3는 BPR Loss를 사용하지 않기 때문에
새로운 손실함수인 "Multi-Modal Contrastive Loss"를 정의합니다.
지금까지 BM3에 대한 간략한 소개를 하였습니다. 본격적으로 BM3에 대해 자세하게 살펴보겠습니다.
▶ Notation (1)
| $\textbf{U}$ | the set of users |
| $\textbf{I}$ | the set of items |
| $\mathbf{e}_u \in \mathbb{R}^d$ | the input ID embeddings of the user $u \in \mathbf{U}$ |
| $\mathbf{e}_i \in \mathbb{R}^d$ | the input ID embeddings of the item $i \in \mathbf{I}$ |
| $d$ | the dimension of ID embedding vector |
| $|\mathbf{U}|, |\mathbf{I}|$ | the cardinal numbers |
| $\mathbf{M}$ | the full set of modalities |
| $\mathbf{e}_m \in \mathbb{R}^{d_m}$ | the modality-specific features obtained from the pre-trained model |
| $d_m$ | the dimension of the features |
| $|M|$ | the cardinal numbers of $\textbf{M}$ - $m$: image or text $\to e_m, e_t$ |
▶ Notation (2)
| $G=(V,E)$ | Graph |
| $V = \mathbf{U} \bigcup \mathbf{I}$ | the node set |
| $E$ | the edge set |
| $|V|$ | the number of nodes |
| $|E|$ | the number of edges |
| $A \in \mathbb{R}^{|V| \times |V|}$ | the adjacency matrix |
| $D$ | the diagonal matrix |
| $H^l \in \mathbb{R}^{|V| \times d}$ | the ID embeddings at the $l$-th layer by stacking all the embeddings of users and items at layer $l$ - the initial ID embeddings $H^0$: is a collection of embeddings $\mathbf{e}_u$, $\mathbf{e}_i$ from all users and items |
0. Boostrapped Multi-Modal Model(BM3)
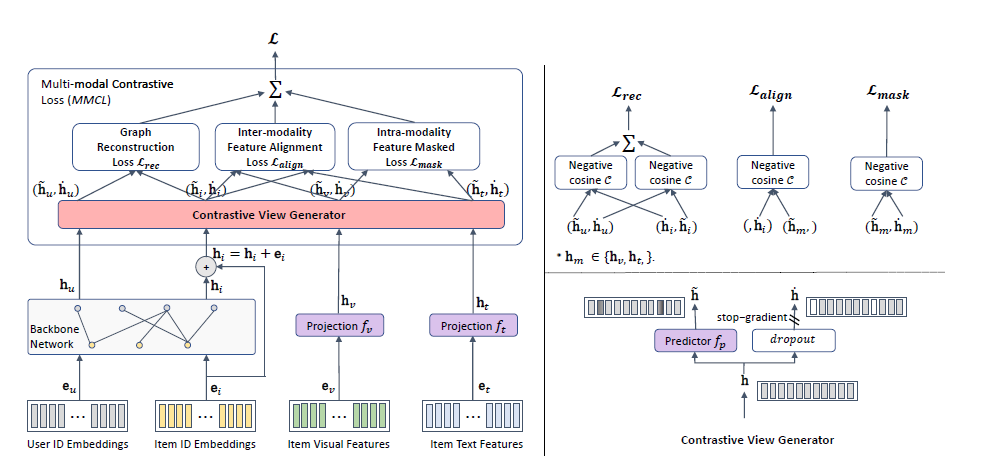
Boostrapped Multi-Modal Model(BM3)를 크게 3가지로 나누어 설명하겠습니다.
- multi-modal latent space converter
- 각 multi-modal features의 차원과 ID embedding vector차원이 다릅니다($\to d_v \ne d_t \ne d$).
- $d_v = d_t = d$로 만들어 주기 위해 multi-modal feature인 $\mathbf{e}_v$와 $\mathbf{e}_t$를 사영시킵니다.
- [Projection] $\mathbf{e}_v, \mathbf{e}_t$는 "Multi-Layer Perceptron(MLP)"를 사용하여 ID embedding vector의 차원인 $d$ 차원으로 만들어줍니다 (산출값: $h_v \in \mathbb{R}^d, h_t \in \mathbb{R}^d$)
- 서로 다른 노드 간의 관계(사용자-아이템 관계)를 반영하여 각 노드(사용자, 아이템)의 representation vector를 학습하기 위해 Light GCN을 사용합니다.
- [Light GCN] User ID embedding vector와 Item ID emebdding vector는 Light GCN을 통하여 서로 다른 노드(node, vertex)간의 관계(사용자와 아이템 간의 관계)를 학습합니다. (산출값: $h_u \in \mathbb{R}^d, h_i \in \mathbb{R}^d$)
- contrastive view generator
- BYOL은 2개의 뉴럴 네트워크인 online network와 target network를 사용하였으며 target network에는 stop gradient 전략을 사용했습니다.
- 반면, BM3는 target network를 제거하고 대신 dropout mechanism을 사용하였습니다.
- multi-modal contrastive loss
1. Multi-Modal Latent Space Converter
Multi-modal features $\mathbf{e}_v \in \mathbb{R}^{d_v}$, $\mathbf{e}_t \in \mathbb{R}^{d_t}$와 ID embedding vector $\mathbf{e}_u, \mathbf{e}_i \in \mathbb{R}^d$의 차원을 동일하게 만들어주는 단계입니다.
1.1 Multi-Modal Features
서로 다른 모달리티에서 얻어진 item feature vector는 서로 다른 차원을 가지고 있으며 서로 다른 특성 공간(feature space)에 존재합니다. 따라서, 우리는 이를 ID embedding vector와 같은 latent space에 사영시켜 주어야 합니다.

- 사영 함수(Projection function) $f_m$: Multi-Layer Perceptron(MLP)
$$h_m = e_mW_m + b_m \in \mathbb{R}^d$$
- $W_m \in \mathbb{R}^{d_m \times d}$
- $d_m \in \mathbb{R}^{d}$
- $d$: the dimension of ID embeddings
각 사영된 모달리티별 임베딩 학습 벡터(representation vector) $h_m$은 ID embedding의 차원과 같은 것을 알 수 있습니다.
1.2 To learn the ID Embeddings
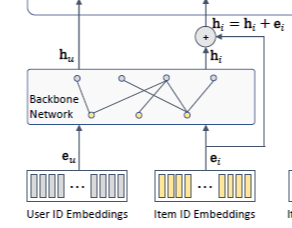
우리가 생성한 그래프 $G=(V,E), V = \mathbf{U} \bigcup \mathbf{I}$는 이분 그래프(Bipartite Graph)입니다.
▶ 이분 그래프(Bipartite Graph)란?
모든 노드가 두 그룹으로 나누어지고(→ User, Item), 서로 다른 그룹의 노드간에는 간선(edge)로 연결되어져 있는 반면 같은 그룹에 속한 노드끼리는 간선으로 연결되어 있지 않은 그래프
만약, 사용자가 아이템을 구매한 내역이 존재하는 경우, 사용자 노드와 아이템 노드간의 간선(edge)으로 연결되어 있습니다. 즉, 간선(edge)에는 사용자와 아이템간의 상호작용이 반영되어 있습니다.
BM3는 "LightGCN"을 사용하여 서로 다른 노드간의 정보를 집약함으로써 각 노드의 embedding vector를 학습합니다.
▶ Feed Forward propagation of GCN
$$h^{l+1} = \sigma(\hat{A} h^l W^l)$$
- $h^{l+1}$: $l$-th layer의 hidden ID embedding vector
- $\sigma(\cdot)$: a non-linear activation function
- $\hat{A} = \hat{D}^{-1/2}(A+I)\hat{D}^{-1/2}$: the re-normalization of the adjacency matrix $A$
- $\hat{D}$: the diagonal matrix of $(A+I)$
LightGCN은 추천시스템의 성능을 저하시키는 GCN의 두 가지 요소를 제거한 모델입니다.
- Linear Transformation $W^l$을 제거하였습니다.
- 활성화 함수 $\sigma$를 제거하였습니다.
▶ Feed Forward propagation of LightGCN
$$h^{l+1} = \hat{A}h^l $$
- $\hat{A} = \hat{D}^{-1/2}(A+I)\hat{D}^{-1/2}$: the re-normalization of the adjacency matrix $A$
- $\hat{D}$: the diagonal matrix of $(A+I)$
LightGCN의 경우, final embedding vector 생성 시 "readout function"을 사용합니다.
※ BM3 논문에서는 readouf function으로 평균 함수(mean function)을 디폴트 값으로 사용하였다고 합니다.
※ Readout function으로는 미분가능한 함수이면 어떠한 함수도 가능합니다.
즉, 모든 $l \in \{1,2, \cdots, L\}$번째 layer에서 생성된 embedding vector $H^l_u, H^{l}_i$를 종합합니다.
Item final embedding vector의 경우, 더 깊고 복잡한 뉴럴 네트워크에서 일반화된 성능을 이끌어내 도움을 주는 residual connection도 추가하였습니다.
$$h_u = \text{READOUT}(h^0_u, h^1_U, \cdots, h^L_u)$$
$$h_i = \text{READOUT}(h^0_i,h^1_i, \cdots, h^L_i) + h^0_i$$
우리는 지금 총 4개의 같은 차원을 가진 (latent) embedding vector를 생성하였습니다.
- $h_u \in \mathbb{R}^d$: user ID embedding vector
- $h_i \in \mathbb{R}^d$: item ID embedding vector
- $h_t \in \mathbb{R}^d$: text-modal item embedding vector
- $h_v \in \mathbb{R}^d$: visual-modal item embedding vector
우리는 이제 고려해야 될 부분은 위 4개의 embedding vector를 어떻게 학습시킬지 입니다.
→ BM3는 Self Supervised Learning 방법론 중 Boostrapped Your Own Latent(BYOL)을 사용하여 학습합니다.
2. Multi-Modal Contrastive Loss
2.1 Contrastive View Generator
BYOL은 두 개의 뉴럴 네트워크로 online network와 target network를 사용합니다.
BM3는 target network를 사용하지 않고 dropout mechanism을 이용합니다.
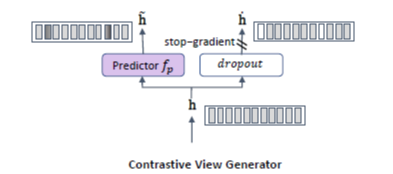
[1]. Online Network for BM3
- online network $f_p$: one-layer MLP
$$\tilde{h} = hW_p + b_p$$
- $h$: (original) embedding vector
- $\tilde{h}$: online embedding vector
- $W_p \in \mathbb{R}^{d \times d}$
- $b_p \in \mathbb{R}^{d}$
[2]. Dropout Mechanism for BM3
$\dot{h} = h \cdot \text{Bernoulli}(p)$
- $h$: (original) embedding vector
- $\dot{h}$: the contrastive latent embedding vector
- $p$: dropout ratio
- BYOL에서의 target network에서처럼, 이 부분에는 stop-gradient를 설정해 줍니다.
그럼 우리는 현재 총 8개의 embedding vector가 존재합니다.
- $(\tilde{h}_u$, $\dot{h}_u)$
- $(\tilde{h}_i$, $\dot{h}_i)$
- $(\tilde{h}_t$, $\dot{h}_t)$
- $(\tilde{h}_v$, $\dot{h}_v)$
BYOL에서는 online network가 target network의 산출값을 예측합니다. 따라서, 두 network의 산출값의 유사도를 기반으로 online network의 파라미터가 업데이트 되도록 손실함수를 정의하였습니다.
BM3에서는 3가지의 손실함수를 정의합니다.
- Graph Reconstruction Loss: $L_{rec}$
- Inter-modality Feature Alignment Loss: $L_{align}$
- Intra-modality Feature Alignment Loss: $L_{mask}$
[Total Loss]
$$L =L_{rec} + L_{align} + L_{mask} + \lambda \cdot (||h_u||^2_2 + ||h_i||^2_2)$$
2.2 Multi-Modal Contrastive Loss
BM3는 입력갑승로 오직 positive user-item pair $(u,i)$를 가집니다.
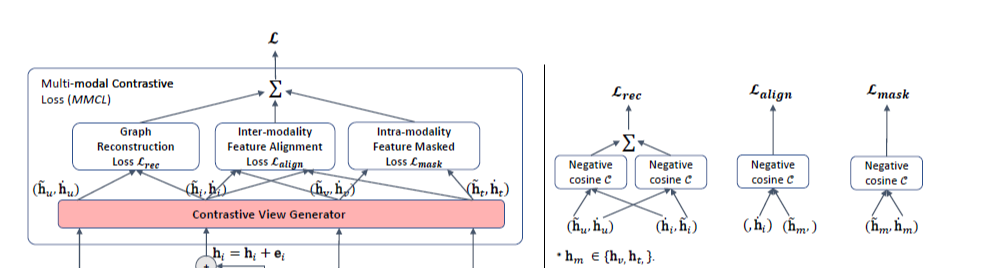
2.2.1 Graph Reconstruction Loss
Graph Reconstruction Loss는 대칭 손실 함수(symmetrized loss function)로
$(\dot{h}_u, \tilde{h}_i)$와 $(\tilde{h}_u, \dot{h}_i)$의 negative cosine similarity를 계산합니다.
$$L_{rec} = C(\tilde{h}_u, sg(\dot{h}_i)) + C(sg(\dot{h}_u), \tilde{h}_i)$$
$$C(h_u, h_i) = - \dfrac{h^T_u h_i}{||h_u||_2 ||h_i||_2}$$
- $|| \cdot ||_2$: L2-norm
- $sg$: stop gradient
- 오직 online embedding vector $\tilde{h}$에 대해서만 파라미터가 업데이트 됩니다.
$L_{rec}$는 사용자 $u$가 주어졌을 때 아이템 $i$를 긍정적으로 선호할 가능성 혹은 그 반대에 대해서 최대화하는 식입니다.
※ 왜 negative cosine similarity를 사용하는가?
- 사용자 $u$와 아이템 $i$간의 유사도를 최대화 해야 합니다
- 따라서, $-1$을 취해줌으로써 손실함수가 최소화되는 방향으로 학습을 진행할 수 있습니다.
※ 오직 online embedding vector만 업데이트 됨 ★ ★
- backpropgation of loss over $(\tilde{h}_u, \tilde{h}_i)$
- no gradient from $(\dot{h}_u, \dot{h}_i)$
2.2.1 Inter-modality Feature Alignment Loss
$$L_{align} = C(\tilde{h}^i_m, \dot{h}^i)$$
- $\tilde{h}^i_m, \, m \in \{t,v\}$: online embedding vector of uni-modal(text or visual....)
- $\dot{h}^i$: contrastive latent embedding of item ID embedding vector $h^i$
각 아이템별 $i$, 각 모달리티별 $m$로 비슷한 특성을 가진 경우는 서로 비슷한 embedding vector를 갖도록 학습하는 손실함수입니다.
2.2.3 Intra-modality Feature Alignment Loss
$$L_{mask} = C(\tilde{h}^i_m, \dot{h}^i_m)$$
우리는 contrastive view generator $\dot{h}^i_m$에서 임의로 특정 원소들을 마스킹합니다(→ dropout mechanism: $\tex{Bernoull}(p)$). 우리는 같은 아이템, 같은 모달리티 하에서 일부분이 마스킹 된 embedding vector $\dot{h}^i_m$와 전체 정보가 들어가 있는 embedding vector $\tilde{h}^i_m$간의 negative cosine similarity를 계산합니다.
$$L_{mask} = C(\tilde{h}^i_m, \dot{h}^i_m)$$
따라서, 최종 손실함수는 다음과 같습니다.
$$L =L_{rec} + L_{align} + L_{mask} + \lambda \cdot (||h_u||^2_2 + ||h_i||^2_2)$$
그렇다면 학습이 끝난 후, 사용자가 $u$가 선호할 상위 $k$개의 아이템은 어떻게 추천하는가?
2. Top-k recommendation
$$s(h_u, h_i) = \tilde{h}_u \cdot \tilde{h}^T_i$$
각 사용자 $u$와 $i$의 학습된 online embedding vector의 내적을 계산합니다. 내림차순으로 정렬 후, 상위 $k$개의 아이템 $i$을 사용자 $u$에게 추천해줍니다.
본 글에서는 Boostrapped Your Own Latent(BYOL)과 Light Graph Convolutional Network(Light GCN)을 사용한 Boostrapped Multi Modal Model(BM3)에 대해 살펴보았습니다.