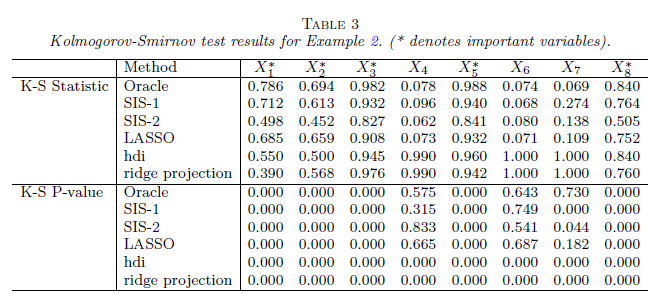
p-value는 통계적 추론에서 중심적인 역할을 하며, 회귀분석에서 회귀계수에 대한 유의성을 판단할 때 사용된다.
고차원 데이터의 경우(n<p), ordinary least square(ols)는 적절하지 않다. 따라서, least square estimator(LSE)를 기반으로 한 회귀계수에 대한 p-value는 타당하지 않다. 이와 같은 경우에 대해 다양한 방법이 제시되었으며 이 논문에서는 oracle p-value를 제안한다. 중요한 변수들이 적은 고차원 데이터에 적용 가능하며 FDR control 하에서 variable selection, variable ranking도 가능하다.
keywords = False Discovery Rate(FDR), high dimensional data, inference, P-value, variable screening
1. Intorduction
현재 많은 데이터가 대부분 고차원 데이터이다. 고차원 데이터란, 변수의 개수(p)가 관찰된 개수(n)보다 큰 데이터를 의미한다.
<Notation>
먼저, 다음 두 가지를 정의한다.
$S^*$ : true model
$ \hat{S} $ : the selected model by as procedure
<Signal-to-noise ratio level>
signal-to-noise ratio level에 따라 3가지로 분류할 수 있다.
첫째, signal이 충분히 강한 경우이다. 이와 같은 경우 model selection consistency를 만족할 수 있다. ($P(S^*=\hat{S})=1$)
둘째, signal이 강하지만 많은 nosie variable이 존재하는 경우다. 이는 screening consistency로 더 약한 결과를 도출한다.(variable screening, $P(S^* \subset {\hat{S}} \to {1})$, $|\hat{S}| \ll {n}$)
셋째, singal이 너무 약해서 중요하지 않는 변수를 구별해 내기 어려운 경우다. 이와 같은 경우, variable screening을 포기하는게 현실적으로 낫다.
<control false positivies>
false positive(잘 못 기각한 것)를 통제하는 접근법에는 the family-wise error rate(FWER), false discovery rate(FDR), false discovery proportion(FDP)이다. 다중 가설 검정에서 FDR-type error rate을 접근하기 위해서는, 유의수준을 할당하는 것은 필수적이다. 다르게 얘기하면, p-value가 필요하다. 저차원 데이터의 경우, p-value가 잘 작동하는 반면, 고차원 데이터의 경우, p-value가 잘 작동하지 않는다. 즉, 귀무가설하에서 p-value는 균일분포를 따른다고 알려져 있는데 고차원 데이터의 경우 이를 만족시키지 못한다. 그래서 논문에서는 고차원 데이터에서 적용 가능한 oracle p-value라는 새로운 개념을 제시한다.
<oracle p-value의 장점>
첫째, 계산적으로 효율적이다.
둘째, 가설 검정 하에서, oracle p-value는 균일분포를 따른다.(oracle p-value $\sim{Unif(0,1)}$)
2. Oracle P-value
우리는 회귀모델을 고려할 것이다.
$Y=(Y_1, Y_2, ... ,Y_n)^t, X = (n*p)$ design matrix
$\beta = (\beta_1, \beta_2, ..., \beta_p)^t, \varepsilon=(\varepsilon_1, \varepsilon_2,...,\varepsilon_n)^t \sim{N_n(0, \sigma^2I_n)}$
$$ Y = X\beta + \varepsilon $$
$S^*$는 앞서 말한 것처럼 true model에 대한 집합이며 다음과 같이 정의할 수 있다. (가정, $S^*$는 sparse, $|S^*|\ll{n}$)
$$ S^* = \left\{j:\beta_j \neq{0}\right\}$$
이제 우리는 $S^*$을 important variable, 그 외의 변수들은 nosie variable이라고 부를 것이다.
<A significance level, or P-value, for each variable can be assigned through the testing hypotheses>
$$ H^0_j: \beta_j=0 vs. H^a_j: \beta_j \neq 0, j=1,..p$$
1. low dimension(n>p): t-분포를 통해 각 변수에 대한 p-value 계산.
2. high dimension(n<p): 위와 같은 과정을 통해서 구한 p-value는 귀무가설 하에서 균일분포를 따르지 않음.
따라서, 논문에서는 계속 얘기했듯이 고차원 데이터에 적용 가능한 oarcle p-value를 제안한다.
<Definition_1>
각각의 $X_j$에 대한 oracle p-value를 다음과 같이 정의한다. ($p^0_j$)
1. If $j \in S^*, p^0_j$ is based on LSE via linear model $Y \sim X_{S^*}$
2. If $j \not \in S^*, p^0_j$ is based on LSE via linear model $Y \sim X_{S^*\cup\left\{j\right\}}$
만약, $j \not \in S^*$ 이면, $p^0_j \sim Unif[0,1]$
하지만, 문제점이 존재한다. 실제로 우리는 important variable set, $S^*$, 에 대해 알지 못한다. 따라서, $S^*$을 추정해야한다.($\hat{S}$ -> SIS-1, SIS-2, LASSO)
3. Mimicking Oracle P-values
우리는 important variable set, $S^*$, 에 대해 알지 못하기 때문에, $S^*$을 추정해야 할 필요성이 존재한다.
[key point]
여기에서 중요한 부분은 $S^*$를 잘 근사하는 집합을 확인하는 것이다.
먼저, $M_j$라는 새로운 집합에 대해 정의해 보고자 한다.
각각의 변수 $X_j$에 대하여, 우리는 다음과 같은 ideal approximation set $M_j$에 대해 선택해야만 한다.
1. if $j \in M_j, p^0_j$ via $Y \sim X_{M_j} $ is to close 0.
2. if $j \not \in M_j, p^0_j$ via $Y \sim X_{M_j} $ is following $Unif]0,1]$
즉, important variable의 p-value 값은 0에 가깝도록, noise variable은 균일분포를 따르도록 $M_j$를 만들어줘야 한다.
일반적으로, 우리는 $M_j = S^*\cup\left\{j\right\}$로 정의하며, $M_j$는 각각의 변수 $X_j$에 대한 $S^*$의 근사치이다.
우리가 $M_j$에 속하는 변수를 선택하기 전에 먼저 다음과 같은 조건을 만들어줘야 한다.
1. 검정 절차는 $M_j$에 속하는 noise variable에 대해 tolerant 해야한다. 다시 말하면, p-value는 $S^* \subset M_j, |M_j| \ll n$을 만족하는 한 타당하다.
2. $M_j$로부터 중요한 변수들의 부재는 절차에 많은 영향을 끼치지 않는다.
3. 각각의 변수 $X_j$에 대하여, 우리는 $S_j \subset S^*, X_{S^*\setminus{S_j}}\perp{X_j}|X_{S_j}$
<Proposition>
다음에서 제시하는 propostion은 noise variable이 균일분포를 따르도록 만들어준다.

위 proposition은 p-value의 공분산 정보가 design matrix X에 대해 완전히 결정되어진다는 것을 보여준다. 이 중요한 정보와 함께 우리는 p-value에 의해 variable rank, variable screening을 하며 정확한 방법으로 FDR을 control한다.
$M_j$를 구축하기 위해서는($M_j = S^*\cup\left\{j\right\}$) 앞서 말했듯이 실제로 중요한 변수들의 집합($S^*$)에 알지 못하므로, 우리는 먼저 집합 $\hat{S}$를 구축하는 것으로부터 시작한다. $\hat{S}$을 추정하는 방법에는 다음과 같은 3가지 방법이 존재한다.(SIS-1, SIS-2, LASSO)

첫번째 방법은 종속변수와의 상관계수가 특정 값(c) 이상이면 $\hat{S}$에 포함시키고 그 외의 변수는 nosie variable로 판단하는 것이다. 두번째 방법은 첫번째 방법에 더하여, important variable로 선택된 변수와 상관관계가 높은 변수도 important variable로 판단하겠다는 것이다. 즉, 첫번째 방법이 두번째 방법보다 더 보수적이다. 세번째 방법은 lasso를 이용하였다.
이제 oracle p-value를 응용한 variable screening과 variable ranking에 대해 살펴보겠다.
4. Applications to variable screening and ranking
<Oracle P-value(ideal case)>
(1). calculate $p^0_j$ for each j=1,..,p
(2). choose a threshold $p^*$ and reject $H_{j0}$ if $p^0_j<p^*$
하지만, 실제로 우리는 $S^*$(important variable set)에 대해 알지 못하므로 oracle p-value를 사용할 수 없다.
따라서, 논문에서는 oracle proxy procedure를 제안한다. 즉, 추정한 중요한 변수들의 집합($\hat{S}$)를 이용한 oracle p-value를 이용하는 것이다.
<Oracle Proxy Procedure>
(1). for each j=1,...,p, find $M_j$ using the procedures proposed in <Definition_1> and calculating $p^0_j$ based on the approximated p-value.
(2). choose a threshold $p^*$ and reject $H_{j0}$ if $p^0_j < p^*$
각각의 시행에서, 우리는 데이터를 두 부분으로 나눈다. 한 부분은 $M_j, j=1,...,p$를 추정하는데 사용하며 한 부분은 $p^0_j$를 추정하는데 사용한다.
$p^0_j$를 얻은 후에는 FDR-control를 하는데 $p^0_j$를 사용할 수 있다.
<Control FDR-type at the target level> -> 3가지 방법 제안(BH-1, BH-2, PFA)
1. Benjamini-Horchberg 1(BH1) method

BH1 방법은 검정 통계량들이 독립적인 경우 잘 작동한다. 즉, 변수들끼리 독립인 경우에 잘 작동한다.
2. Benjamini-Horchberg 2(BH2) method

BH1과의 차이점은 BH2에서는 변수들끼리 independent해도 잘 작동한다. 식을 보면, BH2가 BH1보다 더 보수적인 것을 알 수 있다.
3. PFA
PFA는 FDP를 더 잘 통제할 수 있도록 검정 통계량의 공분산 정보를 이용한 것이다. 공분산 정보를 알고 있는 경우, PFA는 이점을 가지며 FDP를 정확하게 통제한다.
위의 3가지 방법을 통해 variable screening을 할 수 있다.
variable ranking의 경우, important variable은 상위에 noise variable은 하위에 ranking 되어 있다. variable ranking을 통해 variable selection이 가능하다. 오직 상위에 있는 variable만 선택하거나, 하위에 있는 varaible을 버리면 된다. 그렇다면 "top"과 "bottom"을 분류하는 기준은 어떻게 정하는가에 대한 의문점이 들 수 있다. 여기 논문에서는 oracle p-value의 값이 특정 값 이상이거나 이하이거나에 따라 그 기준점을 정하면 된다고 한다.
이제 예시를 통해 설명해 보고자 한다. 처음 예시는 우리가 직접 만든 데이터셋으로 중요한 변수에 대해 알고 있는 경우이고, 두 번째 예시는 실제 데이터 셋으로 중요한 변수에 대해 알지 못 하는 경우이다.
5. Numerical Results.
첫번째 예시
- important variable: x1, x2, x3, x5, x8
- noise variable : x4, x6, otherwise.
먼저, 4가지의 다른 회귀 모형을 만들어줬다.
<첫번째 회귀모형> -> independent predictors
- (n,p,q) = (200, 1000, 5)
- Generate X’s i.i.d from MVN(0,$I_p)$
- Linear Model: $Y_i = \beta_0 + X_i^t\beta + \epsilon_i$, $i = 1,2, ...,n$ with the error $\epsilon \sim N(0, \sigma^2)$
- the error variance $\sigma^2$ is chosen that $R^2 = 0.6$
- true $\beta = (1, 1, 2, 0, 2, 0, 0, -1, 0_{992})$
- true model set : $S^* = \lbrace 1, 2, 3, 5, 8\rbrace$ ↔ $ S^* = \left\{j:\beta_j \neq{0}\right\}$
<두번째 회귀모형> -> AR correlation.
- 첫번째 예시와 같지만, X가 독립이 아니고 서로 상관되어 있다.
- MVN with mean 0 and $Cov(X_j, X_k)=0.5^{|j-k|}$ for $ 1\leq{j,k}\leq{p} $
<세번째 회귀모형> -> weak signal, independent
- 첫번째 예시와 같지만, 두번째 변수($X_2$)가 상대적으로 weak signal이다. 첫번째, 두번째 회귀모형에서는 $X_2$의 회귀계수가 1인 반면에, 세번째, 네번째 회귀모형에서는 $X_2$의 회귀계수가 0.5이다.
- true $\beta = (1, 0.5, 2, 0, 2, 0, 0, -1, 0_{992})$
- true model set : $S^* = \lbrace 1, 2, 3, 5, 8\rbrace$
<네번째 회귀모형> -> weak signal, AR correlation
- 세번째 예시와 같지만, X는 독립이 아니고 서로 상관되어 있다.
- MVN with mean 0 and $Cov(X_j, X_k)=0.5^{|j-k|}$ for $ 1\leq{j,k}\leq{p} $
우리는 oracle p-value가 귀무가설 하에서 noise variable이 균일분포를 따르는지 안 따르는지에 대해 확인해야 한다.
논문에서는 q-q plot과 kolmogorov-smirnov(k-s) test를 통해 확인했다.
k-s 검정통계량은 다음과 같다.
$D_n = sup_x|F_n(x) - F(x)|$
- $F_n(x)$: 우리가 구한 oracle p-value의 누적확률 함수
- $F(x)$: 균일분포의 누적 확률 함수
- ↔ 두 함수의 거리의 최대값 = $D_n$ = K-S statistics
결과는 다음과 같다.
일단, 우리가 검정하고 싶은 것은 귀무가설 하에서 noise variable이 $Unif(0,1)$를 따르는지에 대한 것이다.
<첫번째 회귀모형 검정 결과> -> independent predictors.
- q-q plot
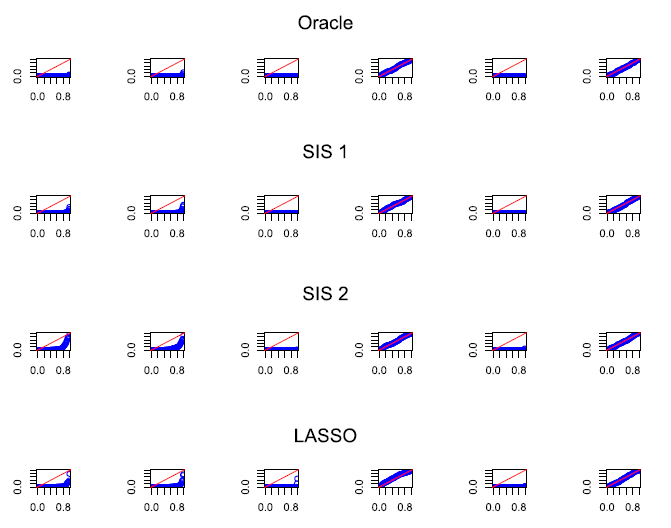
oracle 결과는 실제 oracle p-value 값이며, SIS-1, SIS-2, LASSO는 oracle p-value 값을 근사한 것이다. 4가지 결과 모두 비슷한 것을 확인할 수 있으므로 SIS-1, SIS-2, LASSO가 실제 oracle p-value를 잘 근사하는 것을 알 수 있다.
important variable인 $\left\{x_1,x_2,x_3,x_5\right\}$는 직선에서 벗어나 있는 반면, noise variable인 $\left\{x_4,x_6\right\}$는 직선을 따라가는 것을 알 수 있다. 이는 noise variable의 oracle p-value가 균일분포를 따르는 것을 알 수 있다.

k-s 통계량을 확인해보면, important variable인 $\left\{x_1,x_2,x_3,x_5\right\}$의 p-value 값은 significant한 반면, noise variable인 $\left\{x_4,x_6\right\}$는 non-significant한 것을 알 수 있다. 즉, important variable은 p-value가 균일분포를 따라야 한다는 귀무가설을 기각하고, noise variable은 p-value가 균일분포를 따라야한다는 귀무가설을 기각하지 못 한다. 결론적으로, noise variable의 oracle p-value는 귀무가설 하에서 균일분포를 따라야한다는 가정을 만족한다.
<두번째 회귀모형 검정 결과> -> AR correlation
첫번째 회귀모형 검정 결과와 같은 패턴임을 알 수 있다.

<세번째 회귀모형 검정 결과> -> weak siganl & independent predictors
앞선 모형들과의 차이점은 중요한 변수인 $X_2$가 weak signal이라는 점이다.


중요한 변수인 $X_2$를 주목해서 보면, p-value 값이 0에 가까운 값으로 weak signal을 가진 important variable도 제안된 oracle p-value는 잘 작동한다는 것을 알 수 있다.
<네번째 회귀모형 검정 결과> -> weak signal & AR correlation

지금까지 oracle p-value 값을 통해 중요한 변수인지 아닌지를 판단하는 것을 확인해 보았다. (variable screening)
이제 oracle p-value를 통해 variable ranking을 확인해 보고자 한다.
총 1000개의 변수를 100번 시뮬레이션 한 결과이다.
각 1000개의 변수의 p-value를 구한다음 오름차순으로 정렬한다. ($p^0_{(1)} \leq p^0_{(2)} \leq ... \leq p^0_{(1000)} $)
<첫번째 회귀모형 & 두번째 회귀모형 - variable ranking>
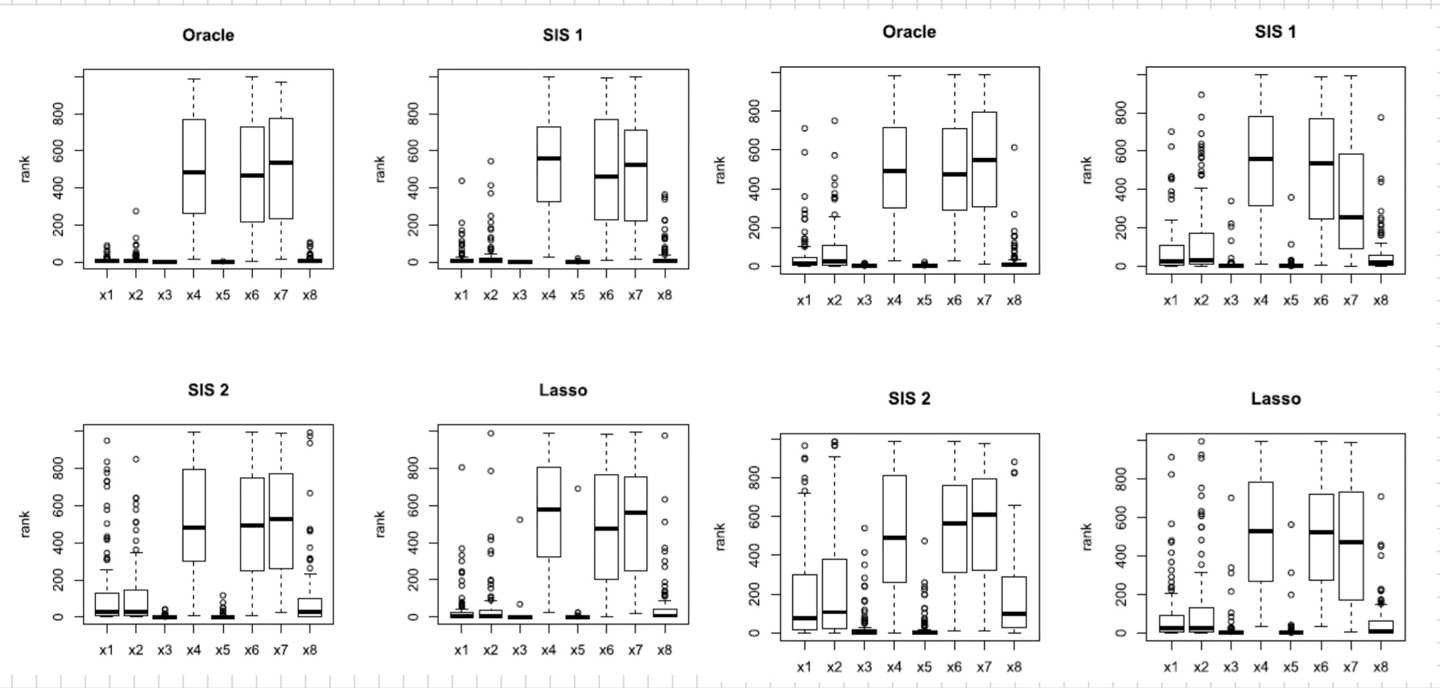
important variable인 $\left\{x_1,x_2,x_3,x_5\right\}$의 rank는 noise variable인 $\left\{x_4,x_6\right\}$의 rank보다 훨씬 작은 것을 확인할 수 있다. 그러므로, noise variable을 선택하기 전에 important variable을 선택함으로써 ranking variable은 잘 작동하는 것을 알 수 있다.
<세번째 회귀모형 & 네번째 회귀모형 - variable ranking> -> weak signal 존재
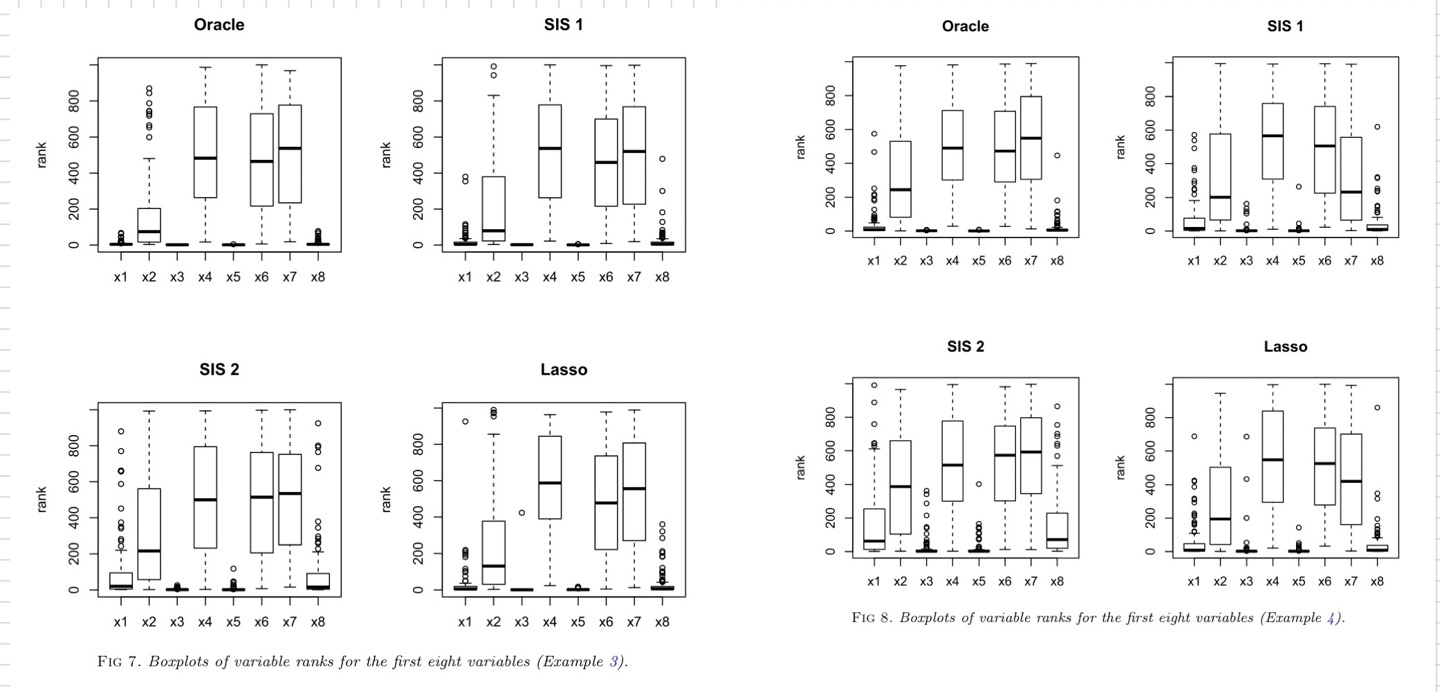
$X_2$를 주목해서 보면, 다른 strong signal을 가진 important variable보다 상대적은 더 큰 rank를 갖지만, noise variable보다 여전히 평균적으로 더 적은 rank를 갖는 것을 알 수 있다. 이는 즉, oracle p-value의 수행은 robust하다는 것을 알 수 있다.
이제는 oracle p-value를 통해 FDR control이 잘 작동하는지 확인해 보고자 한다. 우리는 FDR을 유의수준 0.1로 통제하는 것을 목표로 한다. 네가지 회귀모형 모두 100번의 시뮬레이션을 했으며 true positive(TP), false positive(FP), the average FDR에 대한 결과는 다음과 같다.
False Positive 값을 확인해 보면, FDR을 0.1로 통제 함으로써 2번 중 한 번은 잘 못 기각한 것을 알 수 있다. 또한, BH2가 BH1보다 더 보수적이라고 앞서 말했는데 결과를 보면 확실히 BH2가 PFA와 BH1보다 기각하는 개수(True Positive)가 적은 것을 알 수 있다.
<두번째 예시 - 실제 데이터셋>
이제, 실제 데이터셋을 가지고 oracle p-value가 잘 작동하는지를 확인해 보고자 한다. 즉, 우리는 실제로 중요한 변수 집단($S^*$)에 대해 알지 못한다.
- Dataset: a gene expression data set of Scheetz et al(2006)
이 실험의 목적은 인간의 눈 질병과 관련된 유전자 변형을 확인하는 것이다.
<Experiment>
One primary objective of this study is to identify which gene expression are related to TRIM 32, which is recently found to cause Bardet-Biedl syndrome.↔ 바르테-바들 증후군을 유발하는 것으로 알려진 TRIM 32와 관련된 유전자 발현을 확인하는 것.
- ↔ Bardet-Biedl(바르테-바들 증후군): 망막의 색소성 변성, 다지증, 비만, 학습장애 저하(눈과 관련되 질병)
- response variable = TRIM 32
- Important variable = TRIM 32와 관련된 유전자
- Noise variable = 그 외의 유전자
<key point>
전의 예시와는 달리 이번 예시에서는 실제로 중요한 변수에 대해 알지 못한다.
먼저, 각각의 유전자 TRIM 32와의 correlation 계산을 통해 반응변수와 상관관계가 높은 상위 2000개의 유전자를 추출합니다. 추출된 2000개의 유전자 중에서 important variable과 noise variable를 판단한다. 실제로 important variable에 대해 알지 못 하므로, true oracle p-value를 구할 수 없다. 따라서, oracle p-value를 근사화하는 3가지 방법인 SIS-1, SIS-2, LASSO를 통해 oracle p-value를 계산한다. 추정된 oracle p-value를 통해 각 유전자들의 significant를 판단한다.
<histogram of oracle p-value>

- 0에 가까운 oracle p-values → important variable
- 그 외의 oracle p-values → noise variable → 귀무가설 하에서, 균일분포를 따라야 한다.
논문에 따르면, 매우 작은 oracle p-value를 가진 유전자, 즉 important variable을 제외한 나머지 변수들의 oracle p-value는 균일분포를 따른다고 한다.
이처럼, 매우 중요한 유전자를 추출하는데 과학자들에 유용하다. 예를 들어, LASSO procedure에 따르면, 상위 5개의 중요한 변수로 180, 1428, 1614, 1769, 1868번의 유전자를 선택했다.
6. Discussion
- high dimension linear model에서, 적절한 p-value를 정의하는데 주목을 하고 있다.
- 이 논문에서는, high dimension sparse regression model에서 적용 가능한 oracle p-value를 제안, noise variable의 oracle p-value는 null hypothesis 하에서 $Unif(0,1)$를 따라야한다는 가정을 만족한다.
- Oracle P-value를 구하는데 3가지 방법(SIS-1, SIS-2, LASSO)를 제안한다.
- 더 나아가, fdr를 control 하는 것에 따른 variable screening & variable ranking도 oracle p-value를 이용해 보여준다.
- 이 논문에서 제시한 아이디어는, 다른 절차에도 연장 가능하다.
참고논문: Hao, N., Zhang, H. H. (2017). Oracle P-values and variable screening. Electronic Journal of Statistics, 11(2), 3251-3271
'Statistics' 카테고리의 다른 글
| Variational Inference(변분법) (0) | 2024.06.24 |
|---|---|
| Peak Over Threshold(POT)와 Epsilon Threshold (1) | 2024.02.11 |
| Generalized Linear Model For Count Time Series (0) | 2023.12.11 |


