Generalized Linear Model For Count Time Series

 

 

1. Motivate

본 내용에서 다루고자 하는 주 내용은 count time series를 일반화 선형 모형(Generalized Linear Model: GLM) 접근방법을 이용해 모델링하여 temporal correlation에 대한 파악과 count data $Y_t$에 대한 이산형 주변 분포(discrete marginal distribution)를 구하고자 합니다. Count time series가 포아송 조건부 분포(Poisson conditional distribution)와 음이항 조건부 분포(Negative Binomial conditional distribution)를 따르는 경우에 대해 다룹니다.

 

2. Background

본 section 2에서는 포아송 분포(Poisson distribution)와 음이항 분포(Negative Binomial) 및 일반화 선형 모형(Generalized Linear Model: GLM)에 대해 살펴보고자 합니다.

2.1 Poisson Distribution

포아송 분포는 단위 시간 안에 특정 사건이 일어난 횟수에 대해 모델링할 때 사용됩니다. 

$$\begin{align*}      Y \sim Pois(\lambda), \, \, \lambda > 0, \, \, y=0,1,2, \cdots \end{align*}$$
단위 시간 안에 특정 사건이 일어날 횟수에 대한 기댓값을 $\lambda$라고 했을 때 그 사건이 $y$회 일어날 확률은 다음과 같습니다. 

$$\begin{align*}     P(Y=y) = \dfrac{exp(-\lambda)\lambda^y}{y!}, \, \, E[Y] = Var[Y] = \lambda  \end{align*}$$
포아송 분포의 경우 기대값과 분산이 모두 $\lambda$로 두 값이 같다는 중요한 특성이 존재합니다.

2.2 Negative Binomial Distribution

만약 $Var(Y) > E[Y]$인 경우는 과대산포(over-dispersion)에 대해서 고려하여야 합니다. 이에 대하여 감마 분포(Gamma distribution)를 따르는 $z$가 주어졌을 때 $Y$의 조건부 분포(conditional distribution)는 포아송 분포인 포아송 감마 혼합 분포(Poisson Gamma Mixture Distribution)을 고려할 수 있습니다.

$$\begin{align*}      Y|z \sim Pois(\lambda z) \\      z \sim Gamma(a,b), \\ \end{align*}$$

 

• 형태모수(shape parameter) $a>0$,  척도모수(scale parameter) $b>0$
• $E(Y|z) = Var(Y|z) = \lambda z$, $E(z) = ab, \, Var(z) = ab^2$

$Y$의 평균이 $\lambda$가 되도록 보장하기 위해서($E[Y]=\lambda$), 감마분포의 파라미터 각각을 $a=\nu$와 $b = \dfrac{1}{\nu}$로 정의하면 $Y$의 주변 분포는 음이항 분포를 따릅니다.

$$\begin{align*}      Y \sim NegBin(\lambda, \nu) \end{align*}$$
$$\begin{align*}      f(y;\nu) = \int^\infty_0 f(y|z)f(z;\nu)dz = \dfrac{\Gamma(\nu+y)}{\Gamma(y+1)\Gamma(\nu)} (\dfrac{\nu}{\nu + \lambda})^\nu (\dfrac{\lambda}{\nu+\lambda})^y \end{align*}$$
$Y$의 평균과 분산은 각각 $E[Y]=\lambda$, $Var[Y]=\lambda + \lambda^2/\nu$이며 분산을 확인해보면 $\lambda$에 식 $\lambda^2/\nu$ 이 추가된 것을 확인할 수 있습니다. 즉, $Var[Y] > E[Y]$로 과대산포에 대해서 고려하였음을 알 수 있습니다.

 

2.3 Generalized Linear Model

일반화 선형 모형(GLM)이란 $X = (X_1,X_2, \cdots, X_p)$가 주어졌을 때 반응변수 $Y$의 기댓값 $E[Y]$의 함수와 독립변수 $X$와의 선형관계를 모델링한 회귀 모델(regression model)입니다. 
일반화 선형 모형의 경우, 반응변수의 분포는 정규분포(Normal distribution)뿐만 아니라 이항 분포(Binomial Distribution), 포아송 분포 등도 사용 가능합니다.

$$\begin{align*}     g(E[Y]) = X\beta \end{align*}$$
일반화 선형 모형(GLM)의 구성 요소는 다음 3가지가 존재합니다.

• 확률 요소(Random Component): $y = (y_1, y_2, \cdots, y_n)^T$
  • 반응 변수 $y$의 확률분포는 지수족(Exponential Family)에 속하는 분포이어야 합니다.
• 선형 예측자(Link Predictor):  $X\beta$
  • 선형 예측자는 design Matrix $X$와 Parameter $\beta$의 선형 결합입니다.
  • $X \in R^{n \times p}$, $\beta = (\beta_1, \beta_2, \cdots, \beta_p)^T$
• 연결 함수(Link Function) : $g(\cdot)$
  • $g(\cdot)$는 선형 예측자 $X\beta$와 반응 변수의 기댓값 $E[Y]$을 연결해주는 함수입니다.
  • 연결 함수의 종류에는 항등함수(Identity function), 로짓/시그모이드 함수(Logit/Sigmoid function) 그리고 로그 함수(log function)가 있습니다.

3. Linear Models For Count Time Series

주 내용인 본 section 3에서는 count time series를 일반화 선형 모형(GLM)으로 적합하는 방법에 대해 설명하고자 합니다.

3.1 Poisson Regression Models For Count Time Series

반응변수 $\{Y_t\}$는 count time series이며 서로 상관되어있기(correlated) 때문에 이전 관측치 $F_{t-1} = \{Y_{t-1}, Y_{t-2}, \cdots, \lambda_0\}$가 주어졌을 때의 조건부 분포 $Y_t|F_{t-1}$을 다음과 같이 포아송 자기회귀이동평균(Autoregressive Moving-average : ARMA(1,1)) 모형으로 적합합니다. 

 

$$\begin{align}      Y_t|F_{t-1} \sim Poisson(\lambda_t) \nonumber      \\      \lambda_t = d + a_1 \lambda_{t-1} + b_1Y_{t-1}, t \geq 1 \tag{1} \end{align}$$

• $E[Y_t|F_{t-1}] = Var[Y_t|F_{t-1}]=\lambda_t$
• Generalized Linear Model for Count Time Series
  • $g(E[Y_t|F_{t-1}]) = g(\lambda_t) =  d + a_1 \lambda_{t-1} + b_1Y_{t-1}$
  •  Link function $g(\cdot) = \text{Identity Function}$

조건부 기댓값에 대한 함수는 항등 함수를 사용했으며 조건부 기댓값 $\lambda_t$는 0보다 커야하므로 $d, \{a_1, b_1\} > 0$의 제약조건이 필요합니다. 이제 식 (1)을 이용하여 $Y_t$의 주변 분포를 구하고자 합니다.

$$\begin{align}     Y_t &= \lambda_t + (Y_t - \lambda_t) = \lambda_t + \epsilon_t \nonumber      \\ &= d + (a_1 + b_1)Y_{t-1} + \epsilon_t-a_1\epsilon_{t-1} \nonumber     \\ &= d + (a_1 + b_1)(d+(a_1 + b_1)Y_{t-2} + \epsilon_{t-1} - a_1 \epsilon_{t-2}) + \epsilon_t - a_1 \epsilon_{t-1} \nonumber     \\ &= \cdots \nonumber     \\ &= \frac{d}{1-(a_1 + b_1)} + \sum^\infty_{i=0} (a_1 + b_1)^i\epsilon_{t-i} - a_1 \sum^\infty_{j=0} (a_1 + b_1)^j \epsilon_{t-j-1} \tag{2} \end{align}$$

$Y_t$의 모형은 자기회귀이동평균(ARMA(1,1)) 모형임을 알 수 있으며 정상성(stationary)을 보장하기 위해서 $0<a_1 +b_1<1$의 제약조건이 필요합니다. $\epsilon_t$의 경우 평균, 공분산이 모두 시간 $t$에 의존하지 않기 때문에 White Noise(WN) Process를 따르는 것을 알 수 있습니다.

• $E[\epsilon_t] = E[y_t-\lambda_t] = E[E[y_t-\lambda_t|F_{t-1}]] = 0$
• $Var[\epsilon_t] = Var[E[\epsilon_t|F_{t-1}]] + E[Var[\epsilon_t|F_{t-1}]] = E[\lambda_t] = E[Y_t]$
• $Cov(\epsilon_t, \epsilon_{t+h}) = E[\epsilon_t \epsilon_{t+h}] = E[\epsilon_t E[\epsilon_{t+h} | F_{t+h-1}]] = 0$

식 (2)를 이용하여 $Y_t$의 평균 및 공분산, 상관계수를 구하면 다음과 같습니다.

• $E[Y_t] = \dfrac{d}{1-(a_1 + b_1)} = \mu$
• $Cov(Y_t, Y_{t+h}) = \begin{cases}         \dfrac{(1-(a_1 + b_1)^2 + b_1^2) \mu}{1-(a_1 + b_1)^2} &\text{if } h=0 \\         \dfrac{b_1(1-a_1(a_1+b_1))(a_1+b_1)^{h-1}\mu}{1-(a_1 + b_1)^2} &\text{if } h \geq 1                                     \end{cases}$
  
  • $b_1 = 0$이면 $E[Y_t] = Var[Y_t]$인 반면 $b_1 > 0$에 대해서는 $Var[Y_t] > E[Y_t]$입니다.
    즉, $b_1 > 0$인 경우 과대산포가 존재하며 $Y_t$의 주변 분포는 포아송 분포를 따르지 않음을 알 수 있습니다
• $Corr(Y_t, Y_{t+h}) = \dfrac{b_1(1-a_1(a_1 + b_1))(a_1 + b_1)^{h-1}}{(1-(a_1 + b_1)^2)}$  
  • 제약조건 $\{a_1 \geq 0, b_1 \geq 0, 0 < a_1 + b_1 < 1\}$이 존재하기 때문에 항상 상관계수 $Corr(Y_t, Y_{t+h})> 0$입니다. 즉, 오직 $Y_t$끼리 양의 상관관계를 가졌을 때만 연결 함수 $g(\cdot)$를 항등함수로 사용가능합니다. 만약, 음의 상관관계를 가진 $Y_t$를 고려할 경우 연결 함수 $g(\cdot)$는 로그 함수를 사용하면 됩니다.

3.2 Negative Binomial Models For Count Time Series

$b_1>0$인 경우 과대산포가 존재하는 것을 고려하기 위해 포아송 감마 혼합 모델을 사용합니다. 이전 관측치 $F_{t-1} = \{Y_{t-1}, Y_{t-2}, \cdots, \lambda_0\}$가 주어졌을 때의 조건부 분포 $Y_t|F_{t-1}$을 다음과 같이 음이항 자기회귀이동평균(Autoregressive Moving-average : ARMA(1,1)) 모형으로 적합합니다. 
$$\begin{align}     Y_t|F_{t-1} \sim NegBin(\lambda_t, \nu) \nonumber\\  \lambda_t = d + a_1 \lambda_{t-1} + b_1Y_{t-1}, t \geq 1 \tag{3} \end{align}$$

$Y_t$의 조건부 분포의 평균 및 분산은 각각 $E[Y_t|F_{t-1}] = \lambda_t$와 $Var[Y_t|F_{t-1}] = \lambda_t + \lambda_t^2/\nu$ 같으며 $\lambda_t$에 과대산포를 고려한 식 $\lambda^2_t / \nu$이 추가된 것을 확인할 수 있습니다.
식 (3)을 이용해 $Y_t$의 주변 분포를 구하면 다음과 같습니다.
$$\begin{align} Y_t &= d + (a_1 + b_1)Y_{t-1} + \epsilon_t-a_1\epsilon_{t-1} \nonumber \\ &=\dfrac{d}{1-(a_1 + b_1)} + \sum^\infty_{i=0} (a_1 + b_1)^i\epsilon_{t-i} - a_1 \sum^\infty_{j=0} (a_1 + b_1)^j \epsilon_{t-j-1} \tag{4} \end{align}$$
$\epsilon_t$의 평균, 공분산은 다음과 같으며 포아송과는 다르게 공분산에 식 $E[\lambda_t^2] / \nu$이 존재합니다.

• $E[\epsilon_t] = 0, \,  Cov[\epsilon_t, \epsilon_{t+h}]= 0$
• $Var[\epsilon_t] = Var[E[\epsilon_t|F_{t-1}]] + E[Var[\epsilon_t|F_{t-1}]] = E[\lambda_t + \dfrac{\lambda_t^2}{\nu}] = E[Y_t] + \dfrac{E[\lambda_t^2]}{\nu}$

식 (4)를 이용하여 $Y_t$의 평균 및 공분산, 상관계수를 구하면 다음과 같으며 평균과 상관계수는 $Y_t|F_{t-1}$가 포아송 분포를 따를 때와 같은 반면 공분산의 경우 더 큰 값을 가지는 것을 확인할 수 있습니다. 다만 $\nu \to \infty$($1/\nu \to 0$)라면, 음이항 분포는 포아송 분포로 수렴합니다.

• $E[Y_t] = \dfrac{d}{1-(a_1 + b_1)} = \mu$
• $Cov(Y_t, Y_{t+h}) = \begin{cases}         \dfrac{(1-(a_1 + b_1)^2 + b_1^2)}{1-(a_1 + b_1)^2 - \frac{b_1^2}{\nu}}(\mu + \dfrac{\mu^2}{\nu}) &\text{if } h=0 \\         \dfrac{b_1(1-a_1(a_1+b_1))(a_1+b_1)^{h-1}}{1-(a_1 + b_1)^2-\frac{b_1^2}{\nu}}(\mu + \dfrac{\mu^2}{\nu}) &\text{if } h \geq 1     \end{cases}$
• $Corr(Y_t, Y_{t+h}) = \dfrac{b_1(1-a_1(a_1 + b_1))(a_1 + b_1)^{h-1}}{(1-(a_1 + b_1)^2)}$

4. Model Parameter Estimation

Section 4에서는 로그 우도 가능도 함수를 사용해 모수를 추정하는 방법을 소개하고자 합니다. 지금까지는 ARMA(1,1)에 대해 고려하였다면 모수 추정 부분에서는 더 일반화된 모형 ARMA(p,q)를 고려하고자 합니다.

$$\lambda_t = d + \sum^q_{i=1} a_i\lambda_{t-i} + \sum^p_{j=1}b_jY_{t-j}$$

4.1 Model Parameter Estimation for Linear Poisson Model

먼저 $Y_t$의 조건부 분포가 포아송 분포을 따르는 경우에 대해 로그  가능도 함수는 다음과 같습니다.
$$Y_t|F_{t-1} \sim Poisson(\lambda_t), \, \lambda_t = d + \sum^q_{i=1} a_i\lambda_{t-i} + \sum^p_{j=1}b_jY_{t-j}$$  
$$l(\theta) = \sum^N_{t=1}(-\lambda_t(\theta) + y_t log (\lambda_t(\theta))-log(y_t!)), \, \theta = (d, a_1, \cdots, a_q, b_1, \cdots, b_p)$$
$\theta$는 regression parameter이며 조건부 기댓값 $\lambda_t$는 $\theta$의 의존하기 때문에 시간 $t$에 대한 평균 함수로 정의합니다. 만약, $E[Y_t] = Var[Y_t]$인 경우, 즉, $Y_t$가 포아송 분포를 따르는 경우 $\theta$의 최대가능도추정량(Maximum Likelihood Estimator: MLE) $\hat{\theta}$은 로그 가능도 함수를 최대화하는 $\theta$ 값입니다.
$$\hat{\theta} = argmax_{\theta \in \Theta}l(\theta), \, \Theta = \{d>0, a_i \geq 0, b_i \geq 0, \sum_i a_i + \sum_j b_j < 1\}$$

 

4.2 Model Parameter Estimation for Linear NB Model

$Y_t$의 조건부 분포가 음이항 분포을 따르는 경우에 대해 로그  가능도 함수는 다음과 같습니다.
$$Y_t|F_{t-1} \sim NegBin(\lambda_t), \, \lambda_t = d + \sum^q_{i=1} a_i\lambda_{t-i} + \sum^p_{j=1}b_jY_{t-j}$$  
$$l(\theta;\nu) = \sum^N_{t=1} [log(\dfrac{\Gamma(y_t +\nu)}{\Gamma(y_t+1)\Gamma(\nu)})+\nu log(\dfrac{\nu}{\nu + \lambda_t(\theta)}) + y_t log(\dfrac{\lambda_t(\theta)}{\nu + \lambda_t(\theta)})], \theta = (d, a_1, \cdots, a_q, b_1, \cdots, b_p)$$
추정해야 할 파라미터는 regression parameter $\theta$ 뿐만 아니라 dispersion parameter $\nu$도 존재합니다. $\theta$가 $\nu$에 의존하지 않기 때문에 기존의 최대 우도 가능도 방법을 사용하지 않고 Quasi conditional maximum likelihood 방법을 사용하며 크게 2단계로 이루어집니다. 
첫번째 단계, regression parameter $\theta$를 추정하기 위해 포아송 분포 기반 quasi maximum likelihood를 사용합니다. 제약 조건 하에서 conditional quasi log likelihood function은 다음과 같으며 $l(\theta)$를 최대화하는 $\hat{\theta}$는 Quasi maximum likelihood estimator(QMLE) 입니다.
$$l(\theta) = \sum^n_{t=1} log(p_t(y_t;\theta)) = \sum^n_{t=1} (y_t log(\lambda_t(\theta)) - \lambda_t(\theta)), \, \, \hat{\theta} = argmax_{\theta \in \Theta}l(\theta)$$
$$p_t(y_t;\theta) = P(Y_t=y|F_{t-1}) = \dfrac{\lambda_t^y exp(-\lambda_t)}{y!}, \, t=0,1,2,\cdots$$
두번째 단계, dispersion parameter $\hat{\nu}$은 독립적으로 추정됩니다. QMLE $\hat{\theta}$를 이용하여 조건부 기댓값 $\hat{\lambda} = \lambda_t(\hat{\theta})$을 계산합니다. Christou and Fokianos(2014)에 따르면, 값은 피어슨 카이제곱(Pearson's $\chi^2$) 통계량을 기반으로 된 식 (5)를 만족하는 해(solution)를 $\hat{\nu}$ 값으로 정의합니다.
$$\begin{align}     N-(p+q+1) = \sum^N_{i=1} \dfrac{(Y_t - \hat{\lambda_t})^2}{\hat{\lambda_t}(1+\frac{\hat{\lambda_t}}{\nu})} \tag{5} \end{align}$$
$$\hat{\nu} = (\dfrac{1}{N}\sum^N_{t=1} \dfrac{[(Y_t-\hat{\lambda_t})^2 - \hat{\lambda_t]}}{\hat{\lambda_t}^2})^{-1}$$

5. Experiment

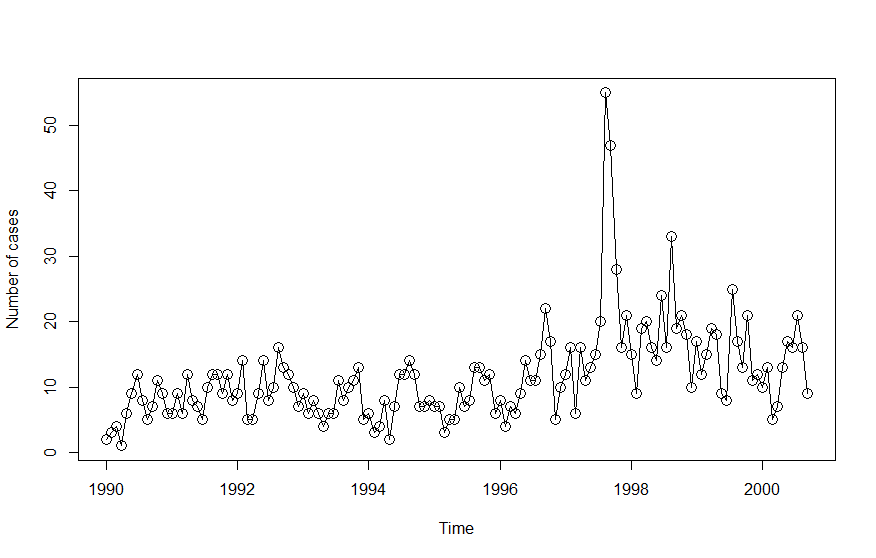
R에서 제공하는 Campy Dataset은 캐나다에서 1990년 1웗루터 2000년 10월까지 한달을 단위로 campylobacterosis 질병에 걸린 횟수에 대한 자료입니다. 일반화 선형 모형(GLM)에 대해서 모형화는 식 (6)과 같습니다.

[Figure 1]

$$\begin{align}     \lambda_t = d + a_{13} \lambda_{t-13} + b_1 Y_{t-1} \tag{6} \end{align}$$
관측치들간의 상관성을 고려하기 위해 일반화 선형 모형에서 이전 관측치 $Y_{t-1}$에 대해 고려하였고 Figure 1을 참조하면 일년마다의 비슷한 패턴이 어느 정도 보여서 조건부 기댓값에 대해서는 $t$ 시점으로부터 $13$개월 이전 시점 $\lambda_{t-13}$에 대해 고려하였습니다. R package tscount에서 제공하는 함수 tsglm을 사용해 포아송 조건부 분포와 음이항 조건부 분포로 적합한 결과는 다음과 같습니다.

install.pacakges("tscount")
library(tscount)
## campy
## > Time Series:
## > Start = c(1990, 1) 
## > End = c(2000, 10) 
## > Frequency = 13 
##   [1]  2  3  4  1  6  9 12 ...     [139] 16  9
########## Model Fitting ##########
campyfit_pois <- tsglm(campy, model=list(past_obs=1, past_mean=13), distr="poisson")
campyfit_nbin <- tsglm(campy, model=list(past_obs=1, past_mean=13), distr="nbinom")

########## Result of Poisson Linear Model ##########
summary(campyfit_pois)

[요약통계량]

> Call:
> tsglm(ts = campy, model = list(past_obs = 1, past_mean = 13), 
    xreg = NULL, distr = "poisson")

> Coefficients:
              Estimate  Std.Error  CI(lower)  CI(upper)
 (Intercept)     2.296     0.6685     0.9855      3.606
 beta_1          0.572     0.0531     0.4680      0.676
 alpha_13        0.217     0.0775     0.0648      0.369
 Standard errors and confidence intervals (level =  95 %) obtained
 by normal approximation.

> Link function: identity 
> Distribution family: poisson 
> Number of coefficients: 3 
> Log-likelihood: -435.4042 
> AIC: 876.8084 
> BIC: 885.6334 
> QIC: 878.0422

"Poisson"	Estimate	Std.Error	CI(lower)	CI(upper)
(Intercept)	2.296	0.6685	0.9855	3.606
beta_1	0.572	0.0531	0.4680	0.676
alpha_13	0.217	0.0775	0.0648	0.369

########## Result of NegBin Linear Model ##########
summary(campyfit_nbin)

[요약통계량]

> Call:
> tsglm(ts = campy, model = list(past_obs = 1, past_mean = 13), 
    xreg = NULL, distr = "nbinom")

> Coefficients:
>              Estimate  Std.Error  CI(lower)  CI(upper)
> (Intercept)     2.296     1.0694     0.1998      4.392
> beta_1          0.572     0.0922     0.3916      0.753
> alpha_13        0.217     0.1265    -0.0312      0.465
> sigmasq         0.112         NA         NA         NA
> Standard errors and confidence intervals (level =  95 %) obtained
  by normal approximation.

> Link function: identity 
> Distribution family: nbinom (with overdispersion coefficient 'sigmasq') 
> Number of coefficients: 4 
> Log-likelihood: -406.0332 
> AIC: 820.0665 
> BIC: 831.833 
> QIC: 890.002

"Negative Binomial"	Estimate	Std.Error	CI(lower)	CI(upper)
(Intercept)	2.296	1.0694	0.1998	4.392
beta_1	0.572	0.0922	0.3916	0.753
alpha_13	0.217	0.1265	-0.0312	0.465
sigmasq	0.112	NA	NA	NA

적합 결과를 확인해 보면, 추정된 회귀 계수 값은 같지만 분산이 $Y_t$의 조건부 분포가 음이항 분포인 경우 더 큰 값을 가지는 것을 확인할 수 있습니다. 또한 추정된 과대산포(sigmasq) 값은 $0.112$로 상대적으로 작은 값을 가집니다. Figure 2를 통해 두 모델의 $Y_t$의 상관계수($Corr(Y_t, Y_{t+h})$)가 같음을 확인할 수 있으며 계절성이나 상관성이 보이지 않는 것을 확인할 수 있습니다.

########## visualization ########## 
plot(campyfit_pois)
plot(campyfit_nbin)

par(mfrow=c(2,1))
acf(residuals(campyfit_pois), main="ACF of Poisson response residuals")
acf(residuals(campyfit_nbin), main="ACF of NegBin response residuals")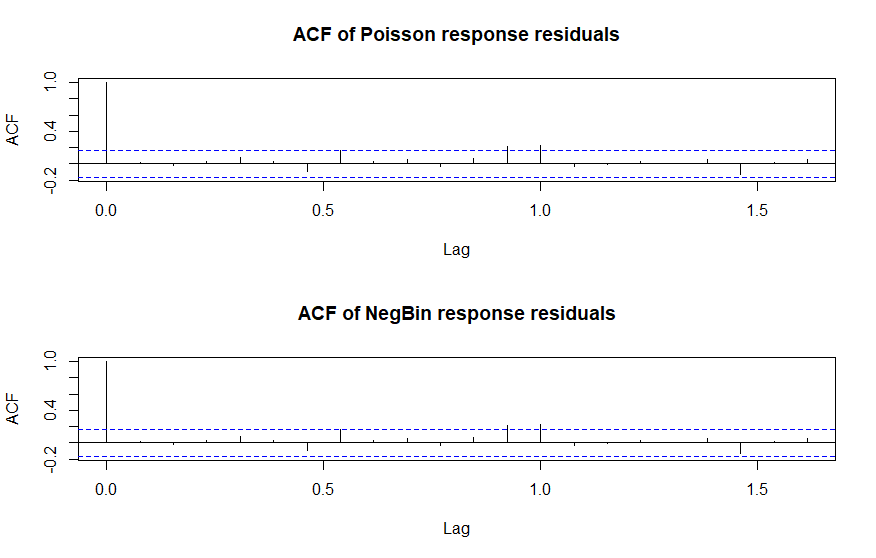

[Figure 2]

두 개의 모델에 대한 성능 평가 방법은 아래 표와 같으며 결과를 확인해 보면 음이항 분포가 모든 성능 평가 지표에서 더 작은 값을 보이므로 Campy Dataset을 적합할 때는 음이항 조건부 분포를 고려하는 것이 더 타당하다는 사실을 알 수 있습니다.

Scoring Rule	Abbreviation	Definition
logarithmic score	logarithmic	$-log(p_t(y_t)$
quadratic score	quadratic	$-2p_t(y_t) + ||p_t||^2$
spherical score	spherical	$-p_t(y_t) / ||p_t||^2$
ranked probability score	rankprob	$\sum^\infty_{y=0}(P_t(y) - 1(y_t \leq y))^2$
Dawid-Sebastiani score	dawseb	$(y_t - \lambda_t)^2/v_t^2 + 2log(v_t)$
normalized squared error score	normsq	$(y_t - \lambda_t)^2/v_t^2$
squared error score &	sqerror	$(y_t - \lambda_t)^2)$

rbind(Poisson=scoring(campyfit_pois), NegBin=scoring(campyfit_nbin))
## >         logarithmic   quadratic  spherical rankprob   dawseb    normsq  sqerror
## > Poisson    3.110030 -0.06888556 -0.2618928 2.687020 4.705391 2.3461116 30.92966
## > NegBin     2.900237 -0.07054600 -0.2636117 2.649399 4.136334 0.9785718 30.92966

	logarithmic	quadratic	spherical	rankprob	dawseb	normsq	sqerror
Poisson	3.110030	-0.06888556	-0.2618928	2.687020	4.705391	2.3461116	30.92966
NegBin	2.900237	-0.07054600	-0.2636117	2.649399	4.136334	0.9785718	30.92966

 

 

 

Reference

[1].Generalized linear models for count time series: Bosowski, Nicholas and Ingle, Vinay and Manolakis, Dimitris (2017)

[2]. Count time series models: Fokianos, Konstantinos (2012)

[3]. tscount: An R package for analysis of count time series following generalized linear models: Liboschik, Tobias and Fokianos, Konstantinos and Fried, Roland (2017)