이번 글에서는 Hyper-Parameter Optimization 방법론 중 하나인 Bayesian Optimization에 대해 다룰 것이다. Hyper-Parameter Optimization이란, 학습을 수행하기 위해 사전에 설정해야만 하는 값인 hyper-parameter의 최적값을 탐색하는 문제이다. Hyper-Parameter의 최적값이란, 학습이 완료된 모델의 일반화 성능을 최고 수준으로 발휘하도록 하는 hyper-parameter 값이다. 학습하는 데이터셋에 따라 같은 모델이여도 hyper-parameter의 최적값은 다르다. 즉, 데이터의 특성을 반영하며 모델의 성능을 높이기 위해서는 hyper-parameter optimization 과정이 필요하다.
- Hyper-Parameter Optimization 종류: Manual Search, Grid Search, Random Search, Bayeisan Optimization
[Bayesian Optimziation]
1. Definition
Bayesian Optmization은 목적함수(loss function, 손실 함수)가 최대 혹은 최소가 되는 최적해를 찾는 방법론이며 매 회 새로운 hyper-parameter 값에 대한 조사를 수행할 시 '사전 지식'을 충분히 반영하면서 동시에 전체적인 탐색 과정을 체계적으로 수행한다. 이 글에서는 목적함수를 최대화하는 것을 초점을 맞추어 정리한 내용이다. Bayesian Optimization은 Bayesian Theorem을 기반으로 생성되었기 때문에 'Bayesian Optimiziation'이라고 불리는 것이다. Bayesian Theorem은 다음과 같다.
$$P(M|E) \propto P(M)P(E|M)$$
$$M: model(or \, \, theory, \, hypothesis), \, E: evidence(or \, \, data, \, observation)$$
Bayesian Theorem은 목적함수를 최적화하는데 핵심 부분이다.
2. Algorithm
일반적으로 목적 함수는 convex하고(아래로 볼록하고) 계산비용이 적게 들어야 한다는 가정이 존재한다. 하지만, 대부분의 목적함수는 이 가정을 만족하지 않는다. 이와 같은 경우, Bayesian Optimization이 유용하다. Bayesian Optimization에서는 입력값과 함숫값에 대해서는 알지만$((x_1,f(x_1)), (x_2, f(x_2)), ...., (x_t, f(x_t)))$, 목적함수 $f$에 대해서는 명시적으로 알지 못하며 하나의 함숫값 $f(x)$를 계산하는데 오랜 시간이 소요되는 경우를 가정하기 때문이다($f = black-box \, function$). 목적 함수 $f$에 대해 모르기 때문에 목적 함수의 도함수에 대해서 알 수 없으며 convex한지 non-convex한지도 알 수 없다. 이러한 상황에서, 가능한 한 적은 수의 입력값 후보들$(\{x_n\})$에 대해서만, 그 함숫값을 순차적으로 조사하여 $f$를 최대로 만드는 최적해 $x^*$를 빠르고 효과적으로 찾는 것이 주요 목표이다.
$$x^* = argmax_xf(x)$$
최적해 $x^*$를 찾기 위해서는 미지의 목적함수를 추정해야 한다. 우리는 Bayesian Theorem을 적용해 미지의 목적함수를 확률적으로 추정할 것이다.
$$P(M|D_{1:t}) \propto P(M)P(D_{1:t}|M) $$
$$D_{1:t} = \{x_{1:t}, f(x_{1:t})\}, \, M \, : Model$$
각 iteration(단계)마다 posterior($P(M|D_{1:t})$)를 최대화하는 데이터($D_{1:t}$)와 prior($P(M)$)을 이용해서 모델로부터 구한 최적화 값과 true global maximum 값과의 차이를 줄여나가는 것이다. 또한, 각 단계마다 posterior는 update된다. 이는 우리가 추정하고 싶은 미지의 목적함수에 근사할 것이다. 예를 들어, 딥러닝 모델의 hyper-parameter인 학습률(learning-rate)의 최적값을 Bayesian Optimization을 통해 찾고자 하는 경우, 입력값인 $x$는 학습률이며 함숫값인 $f(x)$를 모델 성능값으로 설정함으로써, 미지의 목적함수 $f$을 확률적으로 추정해 나아가는 것이다. 앞서 말했던 posterior를 surrogate model이라고 정의할 것이다. Surrogate Model이란, 현재까지 조사된 입력값-함숫값 점들인 $((x_1, f(x_1)), (x_2, f(x_2)), ...., (x_t, f(x_t)))$를 바탕으로 미지의 목적 함수 $f$의 형태에 대한 확률적인 추정을 수행하는 모델을 의미한다.
[Surrogate Model]
Surrogate Model로 가장 많이 사용되는 확률 모델은 Gassuian Process(GP) Model이다. GP는 함수에 대한 분포이며 다변량 정규 분포를 무한 차원의 확률 과정(inifinite dimension stochastic process)으로 확장 가능하다.
$$f(x) \backsim GP(\mu(x), k(x,x'))$$
'Figure 1'에서처럼 반환값은 scalar(상수) 값이 아니라, 정규분포의 평균과 분산이다. 편의성을 위해, 보통 평균함수($m(x)$)는 0으로 설정한다($m(x)=0$). Covariance Function은 다음 2가지 중 하나를 선택하며 주로 RBF 커널을 사용한다.
- the squared exponential kernel(RBF kernel)
$$k(x_i, x_j) = exp(-\dfrac{1}{\theta^2}||x_i-x_j||^2)$$
- Matern Kernel
$$ k(x_i,x_j)= \dfrac{1}{2^{\varsigma-1}\Gamma(\varsigma)}(2\sqrt{\varsigma}||x_i-x_j||^\varsigma H_{\varsigma}(2\sqrt{\varsigma}||x_i-x_j||)) $$
$\Gamma(.)$ and $H_{\varsigma}(.)$ are the Gamma function and the Bessel function of order $\varsigma$.
GP의 핵심은 covariance function $k$이다. $k(x,x')$는 입력값에 대한 유사성/비유사성을 다루기 때문이다. RBF 커널을 예로 들면, $||x_i-x_j||^2$은 입력값들끼리 유사도를 판단하는 함수이다. $x_i$와 $x_j$가 가까울수록 $k(x_i,x_j) \approx 1$이며 $x_i$와 $x_j$가 멀수록 $k(x_i,x_j) \approx 0$이다.
이제 주어진 데이터셋 $\{x_{1:t}\}$에서 데이터를 샘플링한 후, 샘플링된 데이터로부터 Gaussian Process(GP) 모델을 구축한다. 수집된 데이터셋을 $D_t = \{(x_i, y_i), \, i=1,...,t\}$, Gaussian Process 모델을 $y = f(x) + \epsilon, \, f \backsim MultiNormal(0, K)$라고 정의하면, 예측 사후 분포 및 새로운 입력값($x_{t+1}$)에 대한 사후평균과 사후분산은 다음과 같다.
$$P(f_{t+1}|D_{1:t},x_{t+1}) = N(\mu_t(x_{t+1}),\sigma^2_t(x_{t+1}))$$
- $u(x_{t+1}|D_t) = k^t[K+\sigma^2_nI]^{-1}y_{1:t}$ : 데이터셋 $D_t$가 주어진 조건 하에서 임의의 점 $x_{t+1}$에서 추정한 가우시안 프로세스 측정값 $y$의 평균.
- $\sigma^2(x_{t+1}|D_t) = k(x_{t+1},x_{t+1}) - k^t[K+\sigma^2_nI]^{-1}k$ : 데이터셋 $D_t$가 주어진 조건 하에서 임의의 점 $x$에서 추정한 가우시안 프로세스 측정값 $y$의 분산값.
$$k = [(x_{t+1},x_1),..,(x_{t+1},x_t)]$$
$$K = \begin{bmatrix} k(x_1,x_1) & \dots & k(x_1,x_t) \\ \vdots & \ddots & \vdots \\ k(x_t,x_1) & \dots & k(x_t,x_t) \end{bmatrix}$$

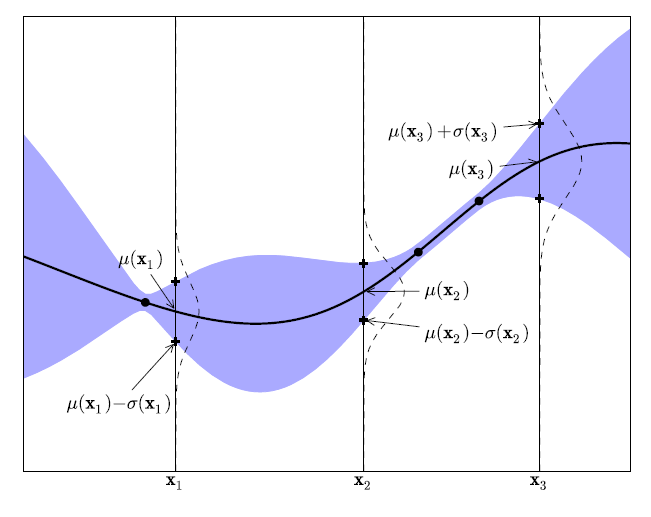
'Figure 2' 그림을 통해 설명하면 다음과 같다. 가로축은 최적화하고 싶은 hyper-parameter 입력값($\{x_{1:t}\}$)이며 세로축은 함숫값 $f(x)$이다. 검은색 점선은 실제 목적 함수, 검은색 실선은 현재까지 조사된 점들 $((x_1,f(x_1)),...,(x_t,f(x_t)))$에 의거하여 추정된 각 $x$ 위치별 평균 $\mu(x)$, 즉 추정된 평균함수이다. 보라색 음영은 각 $x$ 위치별 표준편차 $\sigma(x)$이다. $\mu(x)$의 경우, 현재까지 조사된 점들 $((x_1, f(x_1)), (x_2, f(x_2)), ... , (x_t, f(x_t)))$를 반드시 지나도록 그 형태가 결정되며, 조사된 점에서 가까운 위치에 해당할수록 $\sigma(x)$가 작고, 멀어질수록 $\sigma(x)$ 값이 커진다. 즉, 조사된 점(observation $(x)$)으로부터 거리가 먼 $x$일수록, 이 지점에 대해 추정한 평균값의 불확실성이 크다는 것을 알 수 있다. 또한, 초기 입력값은 2개를 사용했으며 조사된 점의 개수가 점차적으로 증가할수록($t=2 -> t=3 -> 4=5 -> ....$), $\sigma(x)$가 큰 영역의 크기가 점차적으로 감소하여 실제 목적 함수에 대한 추정결과가 점차적으로 압축되는 양상을 보인다. 즉, 조사된 점의 개수가 증가할수록 목적함수의 추정결과에 대한 '불확실성'이 감소하며 최적해 $x^*$를 찾을 가능성이 계속해서 증가한다.
이와 같이 주어진 데이터셋을 가지고 GP 모델을 구축하고 업데이트하는 과정을 반복한다. 지금까지는 Gaussian Process(GP)를 Prior 설정하여 새로운 입력값($x_{t+1}$)에 대한 사후분포를 추정했다. 또한, 우리는 모든 데이터를 사용하지 않고 최소한의 데이터를 사용하면서 매 iteration마다 새로운 입력값으로 GP를 업데이트했다. 그렇다면 다음 iteration에 사용할 후보군(입력값)의 선정은 어떻게 해야하는가? Acquisition function을 이용한다.
[Acquisition Function]
Acquisition Function이란, 목적함수에 대한 현재까지의 확률적 추정 결과를 바탕으로 '최적 입력값 $x$'를 찾는데 있어 가장 유용할 만한 다음 입력값 후보 $x_{t+1}$을추천해 주는 함수를 지칭한다. Acquisition Function을 최대화하는 관측값이 다음 iteration에 사용될 관측값으로 선정된다. Acquistion Function의 종류 및 과정에 대해 살펴보기 전에 'exploitation'과 'exploration'의 개념에 대해 짚고 넘어가야 한다.
- exploitation: 현재까지 조사된 점들 중 함숫값이 최대인 점 근방에서 다음 후보군을 찾는 전략
- exploration: 현재까지 추정된 목적 함수 상에서 표준편차가 최대인 점(불확실성이 큰 점) 근방에서 다음 후보군을 찾는 전략
exploitation과 exploration은 trade-off(상충관계)이며 exploitation과 exploration 간의 상대적 강도를 적절하게 조절하는 것은 실제 목적 함수에 대한 성공적인 최적 입력값 탐색에 매우 중요하다. Acquisition Function의 종류에는 Probability Improvement(PI), Expected Improvement(EI), Confidence Boundary Criteria로 LCB($x$), UCB($x$)가 존재한다.
1. Probaility Improvement(PI)
현재 iteration까지의 최대 함숫값을 $f(x^+)$라고 정의할 것이다($x^+ = argmax_{x_i \in x_{1:t}}f(x_i)$). PI는 $f(x^+)$보다 더 큰 함숫값을 도출할 확률이다. $\Phi(x)$는 누적 정규확률분포이다.
$$PI(x) = P(f(x) \geq f(x^+)) = \Phi(\dfrac{\mu(x)-f(x^+)}{\sigma(x)})$$

'Figure 3'에서 초록색 음영 부분이 PI 값이다. 후보 입력값 $x_3$가 다음 입력값으로 채택된 경우, 초록색 음영 영역이 커질수록 기존 점들보다 더 큰 함숫값을 얻을 가능성이 높아질 것이다. 즉, 목적 함수의 최적 입력값을 찾는데 있어 $x_3$가 '가장 유용할 만한' 후보라고 판단한다. 결점은 식에서 볼 수 있듯이 exploitation만 고려하고, exploration은 고려하지 않는다는 점이다. 해결방안으로 exploration과 exploitation간의 trade-off 관계를 조절하는 새로운 모수 $\xi \geq 0$를 추가해주었다. $\xi$ 값은 사용자가 설정해줘야하는 몫이다.
$$PI(x) = P(f(x) \geq f(x^+) + \xi) = \Phi(\dfrac{\mu(x) - f(x^+) - \xi}{\sigma(x)})$$
여전히 PI에는 $\xi$ 값에 예민하다는 문제점을 가지고 있다. $\xi$ 값이 매우 큰 경우, 탐색이 너무 국소적으로 이루어지는 반면, $\xi$ 값에 매우 작은 경우, 탐색이 너무 전역적으로 이루어져 최적의 다음 후보 입력값을 찾는데 시간이 걸린다.
2. Expected Improvement(EI)
EI는 현재까지 추정된 목적 함수를 바탕으로 어느 후보 입력값 $x$에 대하여 '현재까지 조사된 점들의 함숫값' $f(x_1),...,f(x_t)$ 중 최대 함숫값 $f(x^+)=max_{x_i}f(x_i)$보다 더 큰 함숫값을 도출할 확률(Probability of Improvement(PI)) 및 그 함숫값과 $f(x^+)$ 간의 차이값을 고려하여 해당 입력값 $x$의 '유용성'을 나타내는 값을 출력한다.
$$ EI(x) = \begin{cases} (\mu(x)-f(x^+)-\xi)\Phi(Z)+\sigma(x)\phi(Z) &\text{if } \sigma(x)>0 \\ 0 &\text{if } \sigma(x)=0 \end{cases} \\ Z = \dfrac{\mu(x)-f(x^+)-\xi}{\sigma(x)} $$
$\Phi(x)$는 누적 표준정규분포, $\phi(x)$는 표준정규분포이다. EI는 exploitation과 exploration 사이의 trade-off 관계를 균형있게 맞춰준다. EI는 $\xi=0.01$로 설정한 경우, 대부분의 경우 잘 작동하는 것으로 알려져 있다.
2. Confidence Boundary Criteria
$$ LCB(x) = \mu(x) - \kappa\sigma(x), \, \kappa>0 \\ UCB(x) = \mu(x) + \kappa\sigma(x),\, \kappa>0 $$
$\kappa$는 exploitation과 exploration의 trade-off 관계를 조절하는 모수이다. 큰 값의 $\kappa$는 exploration에 더 큰 가중치를 주겠다는 의미이다. 불확실성이 큰 영역의 근방에 있는 $x$의 값을 선호하는 경우 사용하면 된다. 반면, 작은 값의 $\kappa$는 exploitation에 더 큰 가중치를 주겠다는 의미이다. 평균이 최대 혹은 최소인 근방에 있는 $x$를 선호하는 경우 사용하면 된다. 또한, $\mu(x)$ 값이 클수록 함숫값이 최대인 점 근방에서 다음 후보군을 찾을 가능성이 높으며(exploitation) $\sigma(x)$ 값이 클수록 불확실성이 큰 점 근방에서 다음 후보군을 찾을 가능성이 높다(exploration).
합리적인 acquisition function을 선택한 경우, 우리는 좀 더 빠르게 최적해 $x^*$에 근사하기 때문에 acquistion function을 선택하는 건 중요하다.
최종적으로, Bayesian Optimization 알고리즘을 정리하면 다음과 같다.


- 일단, 우리는 입력값과 함숫값은 알지만($(x_1, f(x_1), (x_2, f(x_2)), ..., (x_t, f(x_t)))$), 목적 함수 $f$에 대해서 모른다.
- 사전 분포를 가우시안 프로세스로 설정 → 기존의 데이터셋을 통해 구축된 GP 모델로 새로운 관측값($x_{new}$)에 대한 사후 분포 추정 → 가우시안 프로세스 모델 업데이트함으로써 미지의 목적 함수에 근사하게 되고 우리의 목표는 우리가 찾은 최적해 $f(\hat{x})$가 실제 최적해 $f(x^*)$에 근사하는 것.
- 목적함수 $f$에 대해 사전 분포를 설정. 우리는 사전 분포를 Gaussian Process로 설정. 각 step마다 새로운 입력값($x_{new}$)에 대한 사후 평균 및 사후 분산을 추정함으로서 가우시안 모델을 업데이트.
- 다음 step에 사용할 새로운 입력값은 acquisition function $\alpha(x)$을 통해 선정. $\alpha(x)$은 평가하기도 쉽고 미분하기도 쉽기 때문에 최적화하기 쉬움.
- 수렴할 때까지 반복.
- acquisition function을 통해 다음 입력값을 선정. : $x_{n+1} = argmax \alpha(x)$
- $f(x_{n+1})$에 대해 평가하고 사후 분포 업데이트.
[참고자료]
- Brochu et al., A tutorial on Bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning.
- https://www.cognex.com/ko-kr/blogs/deep-learning/research/overview-bayesian-optimization-effective-hyperparameter-search-technique-deep-learning-1
'Deep Learning > Optimization' 카테고리의 다른 글
| [Unconstrained Optimization]: Gradient Descent(2) 설명 (0) | 2024.01.10 |
|---|---|
| [Unconstrained Optimization]: Gradient Descent (1) 설명 (0) | 2024.01.10 |

