[Unconstrained Optimization]: Gradient Descent(2) 설명

 

Gradient Descent

Gradient Descent에 대한 전반적인 내용은 이전글에서 살펴보았습니다.

▶ [Goal of unconstrained optimization]

$$\min_\theta f( \theta ), \\ f( \theta ): \mathbb{R}^n \to \mathbb{R}$$

Unconstrained optimization은 어떠한 제약조건이 없는 convex 혹은 non-convex이고 differentiable(미분 가능한) 함수 $f$의 optimal $ \theta^*$를 찾는게 목적입니다.

 

▶ Algorithm

$$\begin{align*} \theta^{(k)} &\gets \theta^{(k-1)} - t_k \nabla f(\theta ^{(k-1)})
\end{align*}
\\
 k=1,2,3, \cdots, t_k > 0$$

• $t_k$: step size or learning rate
• $d_k = - \nabla f(\theta^{(k-1)})$: search direction
• 초기값 $\theta^{(0)} \in \mathbb{R}^n$은 랜덤하게 선택합니다.

[Search direction(탐색 방향)]

Gradient Descent의 경우 탐색 방향 $d_k$는 gradient의 반대 방향(음수 방향) $-\nabla f(\theta^{(k-1)})$입니다.

 

[Step size or learning rate]

Step size $t_k$는 고정 크기 방식과 곡면에 따라 adaptively(다르게) 선택하는 방식이 존재합니다. 만약, step size를 작게 설정한 경우 수렴 속도가 느린 반면 크게 설정한 경우 overshoot, zig-zag 현상이 발생합니다.

 

▶ Problem of gradient descent

[단점 1]. 함수 $f$가 복잡한 경우 수렴속도가 굉장히 느리다는 단점이 존재합니다.

[단점 2]. Local minimum 문제

[단점 3]. Saddle Point(안장점)

---

본 글에서는 (Stochastic gradient descent) 변형 알고리즘인 Momentum, Adagrad, RMSprop, Adam에 대해 살펴보고자 합니다. 4가지 방법론 이외에도 NAG, Adadelt, Nadam 등이 존재합니다.

[Figure 1] Gradient Descent 변형 알고리즘

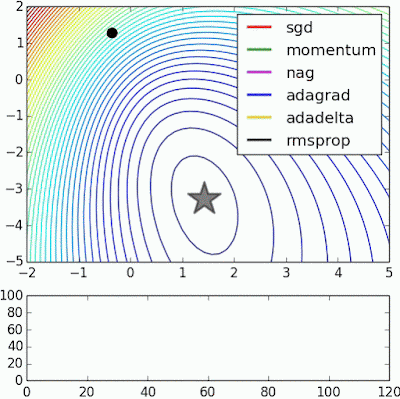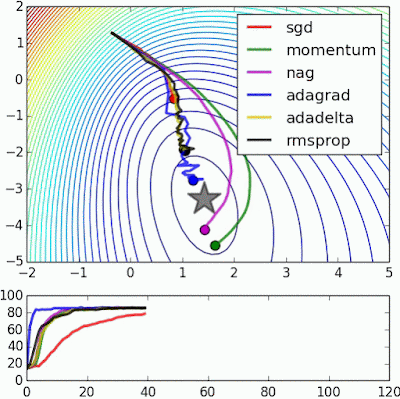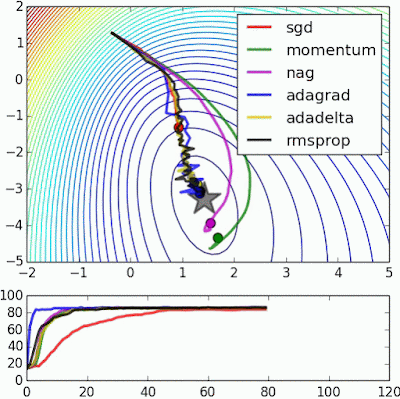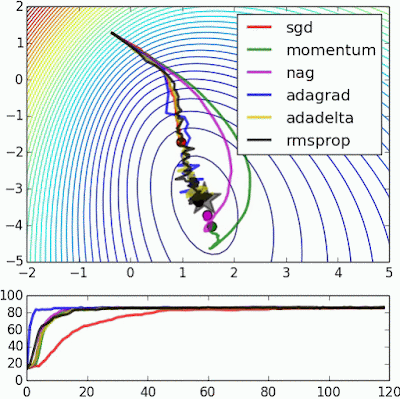
변형	search direction	step size	search direction + step size
(Stochastic) Gradient Descent 변형 알고리즘	Momentum	Adagrad	Adam
	NAG	RMSProp	Nadam
		Adadelt

---

1. Momentum

▶ Idea

Momentum의 main idea는 과거 gradient가 업데이트 되어오던 방향 및 속도를 어느 정도 반영해서 현재 포인트에서 gradient가 0이 되더라도 계속해서 학습을 진행할 수 있는 동력을 제공하는 것입니다.

 

▶ Notation

$$ \color{darkred}{v^{(k)} \gets \gamma_k v^{(k-1)} + t_k \nabla f(\theta^{(k)}) \tag{1}}$$

$$\theta^{(k+1)} \gets \theta^{(k)} - v^{(k)} \tag{2}$$

• $\nu^{(k)}$: 시점 $k$에서의 exponentially weighted moving average 값, 가속도
• $\gamma_k \in (0,1) \approx 0.9$: 관성(moment) 계수
• $t_k=1-\gamma_k \in (0,1)$: step size 또는 learning rate

식 $(1), (2)$를 통해 momentum은 gradient에 관성 $v$을 추가한 형태임을 알 수 있습니다.

• 식 $(1)$: 시점 $k$에서의 기울기와 이전 시점 $k-1$까지 고려한 모멘텀 $v^{(k-1)}$과의 조합
• 식 $(2)$: 모멘텀은 이전 단계에서의 파라미터 업데이트 방향 $\nu ^{(k)}$으로 힘을 받아 현재 단계에서 더 나은 방향으로 파라미터를 조정($\theta^{(k+1)}$)하도록 파라미터 업데이트에 속도 $\nu ^{(k)}$를 도입.

※ [참고] Exponential Weighted Moving Average(지수이동평균)

데이터의 이동 평균 값을 구할 때 오래된 데이터가 미치는 영향을 지수적으로 감소(exponentially decay)하도록 만들어주는 방법

 

▶ [정리] Momentum: parameter $\theta$ update rule에 관성(momentum)을 추가한 형태

• 이전 업데이트 방향도 함께 고려해서 수렴 속도 향상

---

2. Adagrad

▶ Idea

Adagrad는 각 방향마다 step size(learning rate)을 adaptively(다르게) 조정하여 학습 효율을 상승시킨 방법론입니다.

업데이트가 될 때마다 각 parameter $\theta^{(k)}$의 중요도 및 크기가 제각각이기 때문에 동일한 step size(learning rate)을 적용하는 것은 비효율적입니다. 

 

Adagrad는 이에 대하여 학습률 감소(learning rate decay) 기술을 이용합니다.

※ Learning rate decay: 처음에는 크게 학습하다가 점점 작게 학습하는 방법

학습이 적게 된 parameter $\theta^{(k)}$의 step size(learning rate)는 크게 하고 반대로 학습이 많이 된 parameter  $\theta^{(k)}$에 대해서는 step size를 작게 두는 것입니다.

• 학습이 많이 된 parameter $\theta^{(k)}$는 최적값에 근접했을 것이라는 가정하에 작은 크기로 이동하면서 세밀한 값을 조정합니다(slow down the learning rate when an accumulated gradient is large).
• 학습이 적게 된 parameter $\theta^{(k)}$는 step size(learning rate)을 크게 합니다(speed up the learning rate when an accumulated gradient is small).

▶ Notation

$$\mathbf{g^{(k)} = g^{(k-1)} + [\nabla f(\theta^{(k)})]^2} \tag{3}$$

$$\theta^{(k+1)} = \theta^{(k)} - \color{blue}{\dfrac{t_k}{\sqrt{\mathbf{g^{(k)}}+\epsilon}}} \nabla f(\theta^{(k)}) \tag{4}$$

 

식 $(3)$, $(4)$를 통해 각 iteration마다 step size(or learning rate)가 다른 것을 확인할 수 있습니다.

• $g^{(k)}$ 값은 시점 $k$마다(상태가 변할 때마다) 기울기(gradient)의 제곱 값이 계속해서 더해집니다. → 고정된 값 ×
• $\epsilon \approx 1e-6$은 분모가 0이 되는 것을 방지하고자 추가하는 값입니다. → 고정된 값 ●
• $t_k \in (0,1)$는 step size or learning rate → 고정된 값 ●

$g^{(k)}$의 값은 과거 기울기 $\nabla f(\theta^{(k)})$의 제곱 값을 누적해서 더한 값으로 시간이 지날수록 점차 커지는 값입니다. 각 iteration마다 step size(learning rate) $t_k$를 $\sqrt{g^{(k)}+\epsilon}$로 나누어 이동 거리를 조절해줍니다. 시간 $k$가 커질수록 과거의 기울기를 누적해서 더하는 $g^{(k)}$ 값은 점차 커지게 되므로 $\dfrac{t_k}{\sqrt{g^{(k)}+\epsilon}}$ 값은 점점 작아지게 됩니다. 이 부분에서 Adagrad의 idea를 살펴볼 수 있습니다.

• 시간 $k$가 커질수록(→ $\theta$ 학습이 많이 될수록), 작은 크기로 이동( → $\dfrac{t_k}{\sqrt{g^{(k)}+\epsilon}}$ 값이 작음) → 후반에는 작게 이동하면서 학습
• 시간 $k$가 작은 경우 (→ $\theta$ 학습 초반인 경우), 큰 크기로 이동( → $\dfrac{t_k}{\sqrt{g^{(k)}+\epsilon}}$ 값이 큼) → 초반에는 크게 이동하면서 학습

▶ Problem

식 $(3)$을 보면, $g^{(k)}$ 값은 감소하지 않고 계속해서 증가합니다. 즉, 값의 증가만 있는 $g^{(k)}$을 step size(learning rate) $t_k$를 나누는데 사용되기 때문에 $\theta^{(k)}$가 최적해에 근사하지 않았음에도 이동 거리를 계속 작게 만들어  학습을 정제시킵니다.

 

▶ Solution

이에 대한 해결방안으로 RMSProp, Adadelt가 제안되었으며 본 글에서는 RMSProp에 대해 설명하고자 합니다. 

---

3. RMSProp

▶ Notation

$$\color{darkblue}{\mathbf{g^{(k)} = \rho_kg^{(k-1)} + (1-\rho_k)[\nabla f(\theta^{(k)})]^2} \tag{5}}$$

$$\theta^{(k+1)} = \theta^{(k)} - \dfrac{t_k}{\sqrt{\mathbf{g^{(k)}}+\epsilon}} \nabla f(\theta^{(k)}) \tag{6}$$

• $\rho_k \in (0,1) \approx 0.999$: 관성(moment) 계수
• $\epsilon \approx 1e-6$은 분모가 0이 되는 것을 방지하고자 추가하는 값입니다.

RMSProp은 Adagrad에서의 식 $(3)$이 식 $(5)$로 변형된 방법론입니다. 즉, 기울기(gradient)의 제곱 값을 누적해서 더하는 것이 아니라 exponentially weighted moving average 원리를 활용하여 최신 기울기 정보를 더 크게 반영하도록 설정하였습니다.

 

▶ Exponentially weighted moving average 원리

• 과거의 정보 $g^{(k-1)}$는 약하게 반영하고 최신의 정보 $\nabla f(\theta^{(k)})$를 크게 반영하고자 exponentially weighted moving average 사용하였습니다.
• 새로운 모수 $\rho_k$를 사용하여 $g^{(k)}$ 값이 무한히 커지는 것을 방지합니다.
• $\rho_k$ 값이 작을수록 최신의 정보를 더 크게 반영하겠다는 것을 의미합니다.

---

4. Adam: Momentum + RMSProp

Adam은 Momentum과 RMSProp의 각각의 장점을 조합한 방식으로 현재 가장 많이 사용되는 최적화 기법입니다.

• 기울기(gradient)의 과거 변화를 어느 정도 유지함으로써 경로의 효율성을 주는 momentum $v^{(k)}$
• 각 학습 스텝마다 step size(learning rate)을 효율적으로 조정하는 RMSProp $g^{(k)}$

▶ Notation

1. Compute first moment from momentum: $\color{darkred}{v^{(k)} = \rho_1v^{(k-1)} + (1-\rho_1) [\nabla f(\theta^{(k)})]^2}$
2. Compute second moment from RMSProp: $\color{darkblue}{g^{(k)} = \rho_2 g^{(k-1)} + (1-\rho_2)[\nabla f(\theta^{(k)})]^2}$
3. Correct the bias: $\hat{v}^{(k)} = \dfrac{v^{(k)}}{1-\rho_1^k}$, $\hat{g}^{(k)} = \dfrac{g^{(k)}}{1-\rho_2^k}$
4. Update the parameters: $\theta^{(k+1)} = \theta^{(k)} - t_k \dfrac{\hat{v}^{(k)}}{\sqrt{\hat{g}^{(k)}+\epsilon}} $

• $\rho_1 \approx 0.9$, $\rho_2 \approx 0.999$: hyper-parameter
• $v^{(k)}$와 $g^{(k)}$는 momentum 식 $(1)$과 RMSProp 식 $(5)$와 일치하는 것을 확인할 수 있습니다.
• $\hat{v}^{(k)}$, $\hat{g}^{(k)}$: 학습 초기 시 $v^{(k)}$와 $g^{(k)}$가 $0$이 되는 것을 방지하기 위한  보정 값입니다.
• $\epsilon \approx 1e-6$은 분모가 0이 되는 것을 방지하고자 추가하는 값입니다.

▶ Bias Correction(편향 보정)

학습 초기에 $v^{(k)}, g^{(k)}$가 모두 $0$이면 $v^{(k-1)},g^{(k-1)}$도 $0$이고 $\rho_1, \rho_2$는 $1$ 또는 $1$에 가까운 값입니다. 즉, 모멘텀 계수 $\rho_1, \rho_2$의 기여가 거의 없기 때문에 gradient $\nabla f(\theta^{(k-1)})$  값 반영이 거의 없습니다. 이는 최적해가 $0$에 수렴하게 되는 문제가 발생할 수 있습니다. 특히 초기 감소 속도가 작은 경우($\rho$가 $1$에 가까운 경우) 발생합니다. 이를 방지하기 위해 $1-\rho^k$ 값을 나누어 bias를 보정하였습니다. 이와 같은 과정을 편향 보정(bias correction)이라고 합니다.

---

본 글은 gradient descent 변형 알고리즘인 Momentum, Adagrad, RMSProp, Adam에 대해 살펴보았으며 이상으로 마치도록 하겠습니다.

---

[참고자료]

Alec Radford's animations for optimization algorithms

 

Adam Optimizer (Adaptive Moment Estimation)