[Unconstrained Optimization]: Gradient Descent (1) 설명

최적화 기법은 크게 아래 다음 3가지로 분류할 수 있습니다.

▶ [Optimization 종류]

1. Unconstrained Optimization: Gradient Descent
2. Constrained Optimization: Lagrangian Multiply
3. Convex Optimization

본 글은 제한 조건이 존재하지 않은 최적화 방법론(unconstrained optimization) 중 "Gradient Descent" 알고리즘에 대해 설명하고자 하며 [LG Aimers 3기,4기] 강의 및 [모두를 위한 컨벡스 최적화]를 참고하여 작성하였습니다.

 

▶ [Goal of unconstrained optimization]

$$\min_\theta f( \theta ), \\ f( \theta ): \mathbb{R}^n \to \mathbb{R}$$

• optimal value: $f^* = \min_\theta f( \theta )$
• optimal $ \theta^*$

Unconstrained optimization은 어떠한 제약조건이 없는 convex 혹은 non-convex이고 differentiable(미분 가능한) 함수 $f$의 optimal $ \theta^*$를 찾는게 목적입니다.

 

▷ Concept

※ Convex function이란, 위로 혹은 아래로 볼록한 함수를 의미합니다.

※ Global optimum이란, 목표 함수 그래프 전체를 고려했을 때의 최댓값 혹은 최솟값입니다.

※ Local optimum이란, 그래프 내의 일부만 고려했을 때의 최댓값 혹은  최솟값입니다.

※ Proximity term이란, $x$에서 $y$가 얼마나 가까운지를 나타내는 값을 의미합니다.

---

Gradient Descent

▶ Algorithm

$$\begin{align*} \theta^{(k)} &\gets \theta^{(k-1)} - t_k \nabla f(\theta ^{(k-1)})
\end{align*} \tag{1}
\\
 k=1,2,3, \cdots, t_k > 0$$

• $t_k$: step size or learning rate
• $d_k = - \nabla f(\theta^{(k-1)})$: search direction
• 초기값 $\theta^{(0)} \in \mathbb{R}^n$은 랜덤하게 선택합니다.

최적화 기법에서 알고리즘의 수렴 여부와 수렴속도를 결정짓는 매우 중요한 요소는 search direction(탐색 방향) $d_k$와 step size(or learning rate) $t_k$입니다.

 

[Search direction(탐색 방향)]

Gradient Descent의 경우 탐색 방향 $d_k$는 gradient의 반대 방향(음수 방향) $-\nabla f(\theta^{(k-1)})$입니다.

 

[Step size or learning rate]

Step size $t_k$는 고정 크기 방식과 곡면에 따라 adaptively(다르게) 선택하는 방식이 존재합니다. 만약, step size를 작게 설정한 경우 수렴 속도가 느린 반면 크게 설정한 경우 overshoot, zig-zag 현상이 발생합니다.

 

☞ [정리] gradient descent는 gradient의 반대 방향 $-\nabla f( \theta^{(k-1)})$ 으로 step size $t_k$를 잘 조절함으로써 항상 $f$를 최소화하는 값 혹은 지점(local optimum)을 찾을 수 있습니다.

 

 

▷ [Example]

 

왼쪽 그림을 통해,
함수의 기울기(gradient)의 반대 방향(black line)으로 각 곡률마다 다른 step size를 사용하여 global optimum(red point)을 찾는 과정을 볼 수 있습니다.

 

 

 

 

 

---

▶ Interpretation

• 회색 점선: $f(\theta) + \nabla f(\theta)^T(y-\theta) + \dfrac{1}{2} \nabla^2 f(\theta) || y-\theta||^2$
• 검은색 선: 실제 함수 $f$
• 현재 위치 $\theta$: blue point
• 식 $(2)$를 최소화하는 다음 위치 $\theta^+$: red point 

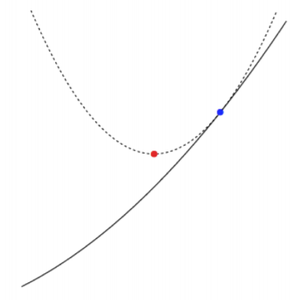
[Step 1]. 오른쪽 그림과 같이 우리는 함수 $f$를 2차 Taylor 식으로 근사할 수 있습니다.

$$f(y) \approx f(\theta) + \nabla f(\theta)^T(y-\theta) + \dfrac{1}{2} \nabla^2 f(\theta) || y-\theta||^2 $$

[Step 2]. Hessian $\nabla^2f(\theta)$을 $\dfrac{1}{t}I$로 대체합니다.

$$\nabla^2 f(\theta)I = \dfrac{1}{t}I \tag{2}$$

식 $(2)$를 통해 step size의 역수인 $\dfrac{1}{t}$는 $\nabla^2f(\theta)$의 eigenvalue인 것을 알 수 있습니다.

$$f(y) \approx f(\theta) + \nabla f(\theta)^T (y-\theta) + \color{darkred}{\dfrac{1}{2t}}|| y-\theta||^2 \tag{3}$$

 

 

 

 

 

~~ 식 $(3)$에 대한 설명 ~~ 

• 함수 $f$를 step size의 역수 $\dfrac{1}{t}$이 eigenvalue인 hessian 행렬을 2차 항의 계수로 갖는 2차 함수로 근사하였습니다.
• 첫번째 term $ f(\theta) + \nabla f(\theta)^T (y-\theta) $은 함수 $f$에 대한 선형 근사식입니다.
• 두번째 term $ \color{darkred}{\dfrac{1}{2t}}|| y-\theta||^2 $은 $x$에 대한 proximity term입니다.

우리는 $\nabla f(y)=0$으로 두고 다음 위치 $y=\theta^+$로 두면 gradient descent algorithm 식 $(1)$을 유도할 수 있습니다.

※식 $(3)$ 양변을 $y$에 대해서 편미분

$$\begin{align*} 
\nabla f(y) &\approx \nabla f(\theta) + \dfrac{1}{t}y - \dfrac{1}{t} x
\\
0 &\approx \nabla f(\theta) + \dfrac{1}{t}\theta^+ - \dfrac{1}{t} x
\end{align*}$$

$$\mathbf{\color{darkblue}{ \theta^+ \gets \theta - t \nabla f(\theta) }}$$

즉, gradient descent는 함수를 $2$차 식으로 근사한 함수의 최소 위치(red point)를 다음 위치로 선택하는 방법입니다
($ \theta^+ = \text{argmin}_y [f(\theta) + \nabla f(\theta)^T(y-\theta) + \dfrac{1}{2} \nabla^2 f(\theta) || y-\theta ||^2$).

• 현재 위치 $\theta$에서 다음 위치 $y=\theta^+$가 얼마나 가까운지는 proximity term의 weight $\color{darkred}{\dfrac{1}{2t}}$에 따라 달라집니다.
  • 만약, $t$ 값이 작은 경우 proximity term의 weight는 커지게 되고 step size는 작아지게 됩니다.

---

▶ Batch gradient descent v.s. Stochastic gradient descent

 

[Purpose]: $f(\theta) = \sum^N_{n=1} f_n(\theta)$를 최소화하는 $\theta^*$를 gradient descent algorithm을 통해 찾는 것

[Gradient upate rule]: $\theta^{(k)} = \theta^{(k-1)} - t_k \nabla f(\theta^{(k-1)}) = \theta^{(k)} - t_k \nabla \sum^N_{n=1}f_n(\theta^{(k-1)})$

 

Optimal $\theta^*$를 찾을 때 각 iteration마다 얼만큼의 데이터 $k \in \{1,2,\cdots, N\}$를 사용하는가에 따라 gradient descent는 크게 다음 3가지로 나눌 수 있습니다.

• Batch gradient descent: 전체 데이터셋 $N$개를 모두 다 사용하는 알고리즘 → $\sum^N_{n=1} f_n(\theta^{(k-1)})$
• Mini-batch gradient descent: 전체 데이터셋의 일부 데이터 $k(k<n)$개만 사용하는 알고리즘→ $\sum_{n \in k} \nabla f_n(\theta^{(k-1)})$  for a suitable choice of $k$, $|k|<n$
• Stochastic gradient descent: mini-batch gradient descent의 일종으로 일부 데이터셋에 대한 gradient의 기댓값이 original full batch gradient 값과 동일하도록, 즉, mini-batch gradient가 original batch gradient에 잘 근사할 수 있도록 디자인된 방법(식 $(4)$)

$$\sum^N_{n=1} \nabla L_n(\theta^{(k-1)}) = E[\sum_{n \in K}\nabla L_n(\theta^{(k-1)})] \tag{4}$$

 

[Stochastic Gradient Descent(SGD)의 보충 설명]

데이터가 엄청 큰 경우, 한 번 step을 내딛을 때마다 너무 많은 계산량을 필요로 합니다. 이를  방지하기 위해 stochastic gradient descent(SGD) 방법이 제안되었습니다. 각 step마다 전체 데이터(batch) 대신 일부 데이터 모음(mini-batch)만을 사용하여 최적화를 진행합니다. SGD의 장점은 다음 2가지가 존재합니다.

1. Batch gradient descent보다 다소 부정확할 수는 있지만 계산 속도가 훨씬 빠르기 때문에 같은 시간에 더 빨리 optimal 값에 근접할수 있으며 여러  반복할 경우 모든 데이터(batch)로 최적화를 했을 결과로 수렴하게 됩니다.
2. Batch gradient Descent에서는 빠질 수 있는 local minimum에 빠지지 않고 더 좋은 방향으로 수렴할 가능성도 높습니다.

---

▶ Problem of gradient descent

(Stochastic) Gradient descent의 몇 가지 단점이 존재합니다. 

[단점 1]. 함수 $f$가 복잡한 경우 수렴속도가 굉장히 느리다는 단점이 존재합니다.

 

 

 

• 가로축: $\theta_1$
• 세로축: $\theta_2$

 

 

 

만약, $\theta_1$과 $\theta_2$에 동일한 step size $t$를 설정한 경우,

• $\theta_1$에 있어서는 접선의 기울기가 크지 않기 때문에 $\theta_1$ 축으로는 상대적으로 변화되는 양이 적습니다(gradient $\dfrac{\nabla f}{\nabla \theta_1}$ 값이 작음).
• $\theta_2$에 있어서는 접선의 기울기가 크기 때문에 $\theta_2$ 축으로는 상대적으로 변화되는 양이 큽니다(gradient $\dfrac{\nabla f}{\nabla \theta_2}$ 값이 큼).

Optimal 값을 찾기 위해 우리가 가야하는 방향은 파란색 선(blue line)입니다. 하지만, gradient descent 알고리즘을 그냥 그대로 사용했을 경우는 지그재그 형태(red line)로 비효율적인 과정으로 필요보다 더 많은 수의 반복 과정을 통해 최종적인 optimal에 도달합니다.

 

[단점 2]. Local minimum 문제

[Figure 1-(a)]. convex function                                                                                [Figure 1-(b)]. non-convex function

Convex function의 경우, 초기 파라미터를 어떻게 설정하여도 gradient descent를 활용하면 최적의 값(optimal)에 도달할 수 있습니다. 또한, convex function의 경우 항상 local minimum은 global minimum이라는 성질이 존재합니다([Figure 1-(a)] 참조).

반면, non-convex function의 경우, 초기점이 어느 곳에 위치하느냐에 따라서 각각 다른 곳에 존재하는 local minimum으로 수렴합니다.

 

[단점 3]. Saddle Point(안장점)

Saddle point(안장점)이란, 기울기(gradient)가 0이지만 극값이 아닌 지점을 의미합니다. Gradient descent의 경우 미분값이 0일 경우($\delta f(\theta) = 0$) 더 이상 파라미터 $\theta$를 업데이트 하지 않기 때문에 안장점을 벗어나지 못한다는 한계점이 존재합니다.

---

▶ Problem of gradient descent

이에 대한 해결방안으로 (stochastic) gradient descent 변형 알고리즘인 Momentum, NAG, Adagrad, RMSProp, Adam 등 다양한 방법론이 제안되었습니다. 이에 대한 설명은 다음글에서 살펴보도록 하겠습니다.

---