본 글에서는 Graph Clustering 방법론 중 'Deep Attentional Embedded Graph Clustering(DAEGC)'를 제안한 [Attributed Graph Clustering: A Deep Attentional Embedding Approach(2019)] 논문을 토대로 설명하고자 합니다.
모델을 설명하기 전 세 가지 개념에 대해 먼저 짚고 넘어가고자 합니다.
[Attributed Graph]
Attributed Graph는 graph structure $(V, E)$와 각 node가 갖고 있는 attribute $X$가 관측된 graph를 의미합니다.
- $G = (V,E,X)$
- $V = \{v_i\}_{i=1,\cdots,n}$: node의 집합
- $E=\{e_{ij}\}$: edge의 집합
- $X=\{x_1;\cdots;x_n\}, x_i \in \mathbb{R}^m$: 각 node가 갖고 있는 attribute value(vector)
[Adjacency Matrix]
Graph structure는 Adjacency matrix(인접행렬) $A \in \mathbb{R^{n \times n}}$로 표현가능합니다.
$$A = \begin{cases}
1 &\text{if } (v_i,v_j) \in E \\
0 &\text{if } (v_i,v_j) \notin E
\end{cases}$$
두 node 사이에 edge가 존재하는 경우($(v_i,v_j) \in E$), 1 아니면 0인 원소를 갖는 행렬입니다.
[Graph Clustering]
Graph Clustering은 graph $G$를 $k$개의 disjoint group $G_1, G_2, \cdots, G_k$으로 분할(partition)하는 것이 목적입니다. 같은 군집(cluster)안에 속하는 node들은 graph structure 상에서 가까이 위치해 있거나 비슷한 attribute value를 가질 가능성이 높을 것입니다.
본격적으로 DAEGC에 대해 설명하고자 합니다.
이 논문에서 던지는 질문이자 attributed graph clustering의 핵심은 다음과 같습니다.
[KEY POINT: How to caputre the structural relationships and exploit the node content(attribute) information?]
결국, 우리에게 주어진 graph의 정보 $A$와 각 node가 갖고 있는 attribute value $X$를 잘 활용해서 clustering 성능을 높이는 것이 목적입니다.
1. Overview
기존의 존재하는 방법론들은 two step framework로 군집화(clustering)을 진행하였습니다.
[Existing Methodologies: Two Step Framework]
- [One step] Attribute value $X$와 structure data $A$를 함께 이용하여 graph embedding을 학습합니다.
- [Two Step] 학습된 graph embedding을 기반으로 clustering을 수행합니다.
논문에서는 two-step framework로 진행되는 기존의 방법론들의 경우, graph embedding 학습시 군집화(clustering)을 목적으로 하지 않기 때문에 최고의 성능에 도달하기 어렵고 graph embedding을 clustering이 잘 되도록 조작(manipulate)하기 어렵다는 문제점을 지적합니다.
[DAEGC: Unified Framework]
이에 대한 해결방안으로 논문에서는 기존과는 다르게 하나의 통합된 프레임워크(Unified Framework) 하에서 graph embedding 학습과 clustering을 수행합니다.

DAEGC는 하나의 통합된 프레임워크(Unified framework) 하에서 크게 2개의 part로 나누어집니다.
- Graph Attentional Autoencoder: 각 노드의 잠재 벡터(latent(feature) representation) $z$를 학습하는 단계
- $z^{(0)} = X$: 각 노드의 잠재 벡터의 초기 값은 각 노드의 특성 값 $X$입니다.
- Self-Training Module: 학습된 잠재 벡터 $z$를 기반으로 graph clustering을 수행하는 단계

[Figure 2]를 참조하면 하늘색 영역(blue area)이 graph attentional autoencoder 부분, 빨간색 영역(red area)이 self-training module 부분입니다.
2. Deep Attentional Embedded Graph Clustering(DAEGC)
본격적으로 DAEGC에 대해 설명하고자 합니다.
2.1 [Part 1]: Graph Attentional Auto-encoder
Graph Attentional Auto-encoder의 입력값과 산출값은 다음과 같습니다. 그래프의 전체적인 구조 정보 $A$와 각 노드가 갖고 있는 특성 값 $X$를 이용하여 각 노드의 임베딩 벡터 $z$를 학습하는 것입니다.
- 입력값(input): graph structure $A$, node attribute value $X$
- 산출값(output): node latent representation vector $z$
Question (1): 그럼 $A$와 $X$를 이용하여 어떻게 각 노드의 임베딩 벡터 혹은 잠재 벡터 $z$를 학습하는가?
이름에서도 알 수 있듯이 크게 두 단계로 Graph Attentional Encoder와 Decoder로 이루어집니다.
2.1.1 Graph Attentional Encoder
[Idea: to learn hidden representations of each node by attending over its neighbors, to combine the attribute values with the graph structure in the latent representation]
'Graph Attentional Encoder'의 아이디어는 각 target node의 임베딩 벡터 $z_i$를 그래프 구조 정보 $A$를 활용하여 neighbor node의 특성 값 $z_j$를 이용하여 학습하는데 이름을 통해 짐작했듯이 다양한 이웃에서 중요한 이웃은 더 큰 가중치를 주어 정보를 가져오자 입니다.
따라서, 우리는 가중치인 "attention score $\alpha_{ij}$"를 계산해야 합니다. 그 전에 먼저 key, query, value에 대해 정의하고 update rule에 대한 식을 서술하고자 합니다.
- Query: $Wx_i(=Wz_i^{(0)}) \in \mathbb{R}^m$: target node의 weight vector
- Key: $Wx_j(=Wz_j^{(0)}) \in \mathbb{R}^m, j \in N_i$: $i$-th neighbor node의 weight vector
- Value: $Wz_j^{(0)} \in \mathbb{R}^m, j \in N_i$: key의 attribute value 값의 weight vector
각 노드의 임베딩 벡터 $z$를 주변 이웃 노드의 정보를 이용해서 업데이트 하는 식은 equation $(1)$과 같습니다.
- Update Rule: $z^{l+1}_i = \sigma(\sum_{N_i}\color{pink}{\alpha_{ij}}Wz^{(l)}_j) \tag{1}$
- $\sigma(\cdot)$: 비선형 함수(non-linear function)
- $N_i$: $i$-th neighbor node의 집합
- $\alpha_{ij}$: target node $i$의 neighbor node $j$의 중요도를 계산하는 attention score(coefficients)
- $Wz_j^{l}$: Value
Question (2): 그럼 어떻게 attention score $\alpha_{ij}$를 계산하는가?
▶ [Attention Score $\alpha_{ij}$]
[1]. Perspective of Attribute value $X$
먼저, 각 neighbor node의 attribute value $x_j$를 합칩니다.
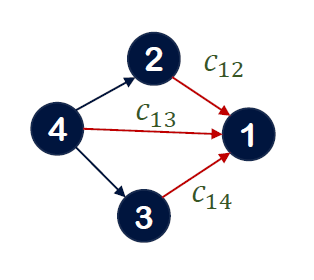

$$c_ij = \vec{a}^T[Wx_i || Wx_j] \in \mathbb{R}$$
- $Wx_i \in \mathbb{R}^m$:Query
- $Wx_j \in \mathbb{R}^m , \, j \ in N_i$: Key
- $||\cdot||$: concatenate
- $\vec{a} \in \mathbb{R}^{2m}$
- 유사도 함수(similarity function): single-layer feedfoward neural network([Figure 3]의 오른쪽 그림 참고)
[2]. Perspective of Topological $A$
기존의 Graph Attentional Network(GAT)의 경우, 오직 1-hop(first-order) neighbor node만 고려하였다면 DAEGC에서는 그래프의 복잡한 관계를 반영하기 위해 더 높은 차수의 이웃까지 고려합니다.
간단한 예시로 살펴보면 다음과 같습니다.

■ 1-hop neighborhood([Figure 4]의 참고)
$$ \text{Adjacency matrix: } A = \begin{pmatrix} 1 & 1 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 1 \end{pmatrix}, \, \text{Degree Matrix : } D = \begin{pmatrix} 0.33 & 0 & 0 \\ 0 & 0.5 & 0 \\ 0 & 0 & 0.5 \end{pmatrix}$$
$$\text{transition matrix: } B = \begin{pmatrix} 0.33 & 0.5 & 0.5 \\ 0. 33 & \color{pink}{0} & \color{pink}{0} \\ 0.33 & 0.5 & 0.5 \end{pmatrix}$$
Transition matrix란, 지금 상태에서 다른 상태로 이동할 확률을 의미합니다. 예를 들어, 3번 node에서 1번 node로 가거나 다시 자기 자신으로 되돌아오로 확률은 0.5인 반면 2번 node로 갈 확률은 $0$입니다.

■ 2-hop neighborhood([Figure 5]의 참고)
$$\text{transition matrix: } B = \begin{pmatrix} 0.44 & 0.42 & 0.42 \\ 0. 11 & \color{pink}{0.17} & \color{pink}{0.17} \\ 0.44 & 0.42 & 0.42 \end{pmatrix}$$
2-hop neighborhood까지 고려할 경우, 3번에서 2번 node로 갈 수 있는 확률이 3번 node ☞ 1번 node ☞ 2번 node가 존재하기 때문에 $0$이 아닌 $0.17$임을 확인할 수 있습니다. 이처럼 high-order neighborhood까지 고려할 경우, 더 많은 neighbor node에 대한 정보를 반영할 수 있습니다.
논문에서는 더 많고 다양한 neighbor node를 고려하기 위해 proximity matrix $M$을 다음과 같이 정의합니다.
$$\text{Proximity Matrix : } M = \dfrac{B + B^2 + \cdots + B^t}{t}$$
- $B$:transition matrix where $ B_{ij} = \begin{cases} 1/d_{i}, &\text{if} e_{ij} \in E \\ 0, &\text{otherwise} \end{cases}$
- $d_i$: the degree of node $i$
$M_{ij}$는 node $i$의 $t$-order까지 고려한 node $j$의 topological relevance 값입니다. 가까이 위치할수록 혹은 더 근접한 이웃일수록 $M_{ij}$의 값은 더 큰 값을 가질 것입니다. 그럼 몇 차 이웃까지 고려할 것인지에 대해서(즉, $t$를 몇으로 설정할 것인가에 대해서) 데이터에 따라 유연하게 선택해야 합니다. 한 가지 더 유의해야 할 점은 $N_i$(node $i$의 neigh bor node 집합)는 인접 행렬(adjacency matrix) $A$에 의해 결정되는게 아닌 $M$의 값이 0이 아닌 원소를 가진 node입니다.
따라서, 최종적으로 $X$와 $A$의 정보를 모두 담은 attentioin score $\alpha_{ij}$는 다음과 같습니다. 서로 다른 node간의 비교를 위해 정규화(normalization)를 수행하는데 있어 softmax function을 사용하였습니다.
$$\alpha_{ij} = \dfrac{exp(LeakyReLU(M_{ij}c_{ij}))}{\sum_{r \in N_i} exp(LeakyReLU(M_{ir}c_{ir}))}$$
- $M = \dfrac{B+B^2+B^3 \cdots + B^t}{t}$
- $c_{ij} = \vec{a}^T[Wx_i||Wx_j]$
▶ [최종정리] Graph Attention Encoder
만약 2개의 graph attention layer를 쌓는 경우 입력값과 산출값은 다음과 같습니다.
- Input: $x_i = z^{(0)}_i$
- $z^{(1)}_i = \sigma(\sum^i_{j \in N_i} \alpha_{ij} W^{(0)}x_i)$
- $z^{(2)}_i = \sigma(\sum^i_{j \in N_i} \alpha_{ij} W^{(1)}z_i^{1})$
- Output: $z=z^{(2)}_i$
2.1.2 Decoder
디코더(decoder) 부분은 graph structure $A$, attribute value $X$ 혹은 둘 다 재건축(reconsctruct)할 수 있습니다. 논문에서는 단순하게 graph structure $\hat{A}$을 inner product decoder를 이용해 재건축합니다.
▶ [최종정리] Decoder
- Input: learned embedding vector $z$
- output: $\hat{A}_{ij}$
$$\begin{align} \hat{A}_{ij} &= sigmoid(z^T_iz_j) \\ &= \dfrac{1}{1+exp(-z^T_iz_j)} = \dfrac{exp(z_i^Tz_j)}{1+exp(z^T_iz_j)}\end{align}$$
2.1.3 Loss Function(Reconstruciton error): Binary Cross Entropy Loss
"Graph Attentional Auto-encoder" part의 손실함수는 이진 분류(binary classification) 손실 함수로 대표적으로 사용되는 "Binary Cross Entropy Loss"를 사용합니다.

$$\begin{align}L_r &= \sum^{N_v} BCELoss(A_{ij}, \hat{A}_{ij}) \\ &= \sum^{N_v}_{i=1} -(A_{ij}log(\hat{A}_{ij})+(1-A_{ij})log(1-\hat{A}_{ij})) \end{align} \\ A_{ij} \in \{0,1\} \, \hat{A}_{ij} \in (0,1)$$
실제값(true label) $A_{ij}$는 0 또는 1의 값, 예측값(predict label) $\hat{A}_{ij}$는 0에서 1 사이의 확률값으로 파란색 선(blue line)은 실제값이 1인 경우에 대한 손실 함수, 주황색 선(orange line)은 실제값이 0인 경우에 대한 손실함수입니다.
만약, 실제값이 1인 경우 예측값이 확률 1에 가까운 경우는 손실이 작게 반대로 0에 가까운 경우 손실이 크도록 준 형태입니다.
결국, 손실함수 $L_r$이 최소화(minimize)되도록 $z$를 학습합니다.
지금까지는 각 node의 잠재 벡터 혹은 임베딩 벡터 $z$를 학습하는 방법에 대해 다루었습니다.
이제 두번째 part인 Self-optimizing clustering에 대해 다루고자 합니다.
▶ [최종정리] Graph Attentional Autoencoder
- Input: graph structure $A$ and node attribute value $X$
- output: $z$ that minimize the reconstruction error
2.2 [Part 2]: Self-optimizing Clustering
Graph clustering의 주된 과제는 다음과 같습니다.
[Main Challenge for graph clustering]
첫째, 비지도 학습으로 현재 군집화 결과가 참인지 아닌지에 대한 label guidance가 존재하지 않습니다.
둘째, 학습된 임베딩 벡터 $z$가 잘 최적화(optimized) 되었는지에 대한 여부를 피드백할 수가 없습니다.
[Solution]
이에 대한 해결책으로 논문에서는 self-optimizing embedding algorithm을 제안합니다.
Part 2 부분은 먼저 손실 함수를 정의하고 설명하고자 합니다.
2.2.1 Loss Function(Clustering Loss): Kullback-Leibler Divergence
$$L_c = KL(P||Q) = \sum_i \sum_u p_{iu} log \dfrac{p_{iu}}{q_{iu}} $$
- $q_{iu}$는 node embedding $z_i$와 각 cluster center embedding $\mu_u(u=1,2, \cdots, k)$ 사이의 유사도를 계산한 값입니다.
- 측정 수단으로 자유도가 1인 'Student t-distribution'을 사용합니다.
즉, $q_{iu}$는 각 노드마다 $\mu$번째 군집에 속할 확률을 나타내는 값으로 soft clustering assginment distribution은 다음과 같습니다.
$$q_{iu} = \dfrac{(1+||z_i - \mu_u||^2)^{-1}}{\sum_k(1+||z_i - \mu_k||^2)^{-1}} \tag{2}$$
분모는 normalization term입니다.
- $p_{iu}$는 target distribution입니다.
$$p_{iu} = \dfrac{q^2_{iu}/\sum_i q_{iu}}{\sum_k(q^2_{ik}/\sum_i q_{ik})} \tag{3}$$
식 $(3)$을 확인해보면, 타겟 분포 $p_{iu}$는 우리가 추정하고자 하는 분포 $q_{iu}$에 의존합니다. 매 iteration마다 학습시 $q_{iu}$가 업데이트 되기 때문에 자동으로 $p_{iu}$도 업데이트 됩니다. 이는 수렴(convergence)의 불안정성을 초래하기 때문에 $q_{iu}$의 경우는 매 5번의 iteration마다 업데이트되도록 설정해주어야 합니다.
Clustering loss는 현재 분포 $Q$가 타겟 분포 $P$에 근접하도록 학습하며 clustering loss가 최소화(minimize)되는 $z$와 $\mu$를 찾습니다. 즉, 여기에서도 각 노드의 임베딩 벡터 $z$가 학습되며 동시에 각 노드의 soft label $\mu$도 학습되는 것입니다("confident assignment" as soft labels to supervise Q's embedding learning).
Part 2에서는 군집화 성능을 높이기 위해 각 노드의 임베딩 벡터 $z$를 manipulate하는 과정이라고 생각하면 될 것 같습니다.
▶ [최종정리] Self Training Clustering
- Input: Learned Emebdding vector $z$
- output: emebdding vector $z$ and cluster center $\mu_u$ that minimize cluster loss
※ ※ 참고 ※ ※
[Pretrain]
군집화를 시행하기 전에 의미있는 임베딩(meaningful embedding) $z = z^{(2)}_i$를 얻기 위해서 "self-optimize clustering" 없이 "Graph attention auto-encoder"만을 학습하는 pretrain 단계가 존재합니다.
또한, 군집화를 하기 위해서는 각 군집의 중심 $\mu_u$의 초기값이 필요합니다. 이를 위해 학습 전 모든 임베딩 벡터 $z$에 대하여 k-means clustering을 한 번 수행해 initial cluster center를 찾습니다.
3. Joint Loss Function
글의 첫 부분 overview에서 말했듯이 DAEGC의 경우 하나의 통합된 프레임워크에서 이루어진다고 말했습니다. 따라서, 우리는 최종적으로 다음과 같이 손실함수를 정의합니다.
[Total Objective Function]
$$L = L_r + \gamma L_c$$
- $L_r$: reconstruction loss
- $L_c$: clustering loss
- $\gamma \geq 0$: coefficient that controls the balance in between
우리는 joint loss function $L$을 최소화하는 $z$와 $\mu$를 학습하는 것입니다.
[Result of clustering]
우리는 마지막으로 최적화된 $Q$ 값을 통해 각 노드마다 $q_{iu}$를 최대화하는 $u$를 찾음으로써 군집 결과를 얻을 수 있습니다. 즉, 다음 식과 같이 각 노드 $v_i$의 label $s_i$를 얻을 수 있습니다.
$$s_i = argmax_{u} q_{iu}$$
논문에서는 DEAGC의 모델의 장점 3가지를 언급합니다.
- Interplay exploitation: auto-encoder기반 graph attention network를 이용함으로써 graph structure $A$와 node attribute $X$에 대한 정보를 함께 잘 이용했습니다.
- Clustering specialized embedding: 군집화 성능을 향상시키기 위해 각 노드의 embedding vector $z$를 self-training clustering을 통해서 manipulate하였습니다.
- Joint Learning: 기존의 방법론들처럼 two-step framework 하에서 수행하지 않고 unified framework 하에서 학습을 진행하였습니다.
본 글은 Graph Clustering 방법론 중 Deep Attentional Embedding Graph Clustering(DAEGC)에서 다루어 보았습니다. 이상으로 마치도록 하겠습니다. 감사합니다.
'Graph(Graph Neural Network)' 카테고리의 다른 글
| Fraud Detection: CARE-GNN (0) | 2024.05.01 |
|---|---|
| Scalable MCMC for Mixed Membership Stochastic Blockmodels (0) | 2022.11.21 |
| GCN - Image Classification (0) | 2022.11.03 |
| Bayesian graph convolutional neural networks for semi-supervised classification (0) | 2022.10.09 |
| Semi-Supervised Classification With Graph Convolutional Networks (0) | 2022.09.19 |



