Graph Neural Network(GNN) based Fraud Detection은 서로 다른 특성을 갖는 이웃 정보를 종합(aggregate)함으로써 각 node가 suspicous(사기꾼)인지 benign(일반인)인지 판단합니다.
▶ Problem Definition
▷ Definition 1: Multi-relation graph
$$G = \{V,X,\{\varepsilon_r\}|^R_{r=1} Y\}$$
- $V=\{v_1,v_2, \cdots, v_n\}$: the set of nodes
- 각 nodes $v_i$는 $d$ 차원의 feature vector를 갖음($x_i \in \mathbb{R}^d$).
- $X = \{x_1,x_2, \cdots, x_n\}$: node-feature matrix
- $e_{i,j}^r = (v_i, v_j) \in \varepsilon_r$: edge between $v_i$ and $v_j$ with a relation $r \in \{1,2, \cdots, R\}$
- 서로 다른 타입을 가진 $R$개의 relation이 존재
- $Y$: the set of labels for each node in $V$
▷ Definition 2: Fraud Detection on Graph
"[2.1] Semi-supervised binary node classification problem"
Node $v_i$는 $0$ 또는 $1$의 라벨을 갖습니다($y_v \in \{0,1\} \in Y$). $0$은 benign(일반인), $1$은 suspicious(사기꾼)을 의미합니다. 또한, label을 갖는 node에 한해서만 학습이 이루어진 후, label을 갖지 않는 node에 대해 사기꾼 여부를 예측하기 때문에 semi-supevised binary node classification problem입니다.
"[2.2] relation R"
Relation은 노드 사이에 연결된 rules, interactions 또는 shared attributes을 의미합니다.예를 들어, 같은 사용자가 두 개의 review를 한 경우, 두 가지의 타입의 relation(Relation I, Relation II)을 갖습니다.
▷ Definition 3: GNN aggregation process
$$h^{(l)}_v = \sigma (h^{(l-1)}_v \oplus \text{Agg}(\{h^{(l-1)}_{v',r}: (v,v') \in \varepsilon^{(l)}_r\}|^R_{r=1})$$
- $v$: center node
- $v'$: neighbor node of node $v$ → $(v,v') \in \varepsilon^{(l)}_r$
- $h^{(l)}_v$: the hidden embedding vector of node v at $l$-th layer
- $h^{(0)}_v=x_v$: node feature vector
- $h^{(l-1)}_{v',r}$: the embedding vector of neighboring node $v'$ under relation $r$
- $\text{Agg}$: a aggregation function that mapping the neighborhood information from different relations into a vector
- 서로 다른 관계(relation)로부터 이웃 정보를 집계하는 함수
- mean function
- attention function
- 서로 다른 관계(relation)로부터 이웃 정보를 집계하는 함수
- $\oplus$: operator that combines the information of $v$ and its neighboring information
- 집계된 이웃 정보(neighbor node)와 타겟 노드(center node)를 합치는 함수
- concatenation
- summation
- 집계된 이웃 정보(neighbor node)와 타겟 노드(center node)를 합치는 함수
각 node의 임베딩 벡터 $h^{(l)}_v$는 이웃 노드의 임베딩 벡터를 집계(aggregation)함으로써 학습합니다.
▶ CARE-GNN
'Enhancing Graph Neural Network-based Fraud Detectors against Camouflaged Fraudsters' 논문에서 제안한 모델인 CAmoutflag-REsistant GNN(CARE-GNN)은 3가지의 모듈을 도입함으로써 GNN aggregation process를 향상시켰습니다.
- Label-aware similarity measure: center node의 neighbor node간의 similarity(유사도) 계산 (→[Section 2.1]).
- Similarity-aware Neighbor Selector: 가장 유사한 $p$개의 neighbor node 선택 (→[Section 2.2]).
- Relation-aware Neighbor Aggregator: 각 relation 하에서 intra-relation aggregator를 통해서 임베딩 벡터(embedding vector) 학습 후 inter-relation aggregator를 통해 서로 다른 relatioin 하에서 생성된 임베딩 벡터를 결합 (→[Section 2.3]).
본 글에서는 앞서 설명한 3가지 모듈에 대한 자세한 설명을 바탕으로 CARE-GNN에 대해 다루고자 합니다.
1. Background
사기꾼(fraudster)들은 사기 시스템을 우회하거나 허위 정보를 분산시키기 위해 일반 사용자로 위장합니다. 이와 같은 사기꾼들을 탐지하는데 있어 Graph Neural Network(GNN)의 효과성이 입증되어 있습니다. GNN은 서로 다른 relation 타입으로 노드들이 연결되어 있으며 사기꾼들은 결국 ""사기""라는 같은 목적을 가지고 활동을 하기 때문에 서로 연결되는 경향이 있다는 근거를 바탕으로 사기꾼들을 탐지합니다. 하지만, 기존의 방법론들은 사기꾼들의 행위를 무시하며 CARE-GNN은 이를 보완한 모델입니다. 사기꾼의 행위는 크게 "Feature camoutflage"와 "Relation camoutflage"로 분류할 수 있습니다.
▶ [Example : construct a graph with two relations(edges) and two types of entities(nodes)]
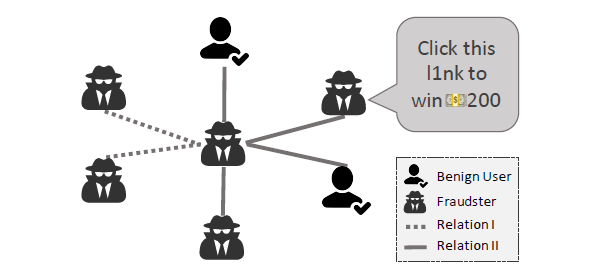
[Figure 1]은 두 타입의 관계(Relation I, Relation II), 두 타입의 노드(benign, suspicous)를 가진 그래프(graph)입니다. 서로 다른 노드끼리 연결된 경우 서로 유사한 특징이 있다고 해석할 수 있습니다.
먼저, "Feature camoutflage"에 대해 살펴보겠습니다.
Feature camoutflage란, 사기꾼들이 특성이나 패턴에 기반 사기 탐지 시스템에서 탐지를 회피하기 위해 사용하는 기술을 의미합니다. 이와 같은 탐지 알고리즘들은 특정한 패턴이나 키워드에 의존하기 때문에 [Figure 1]과 같이 특수 문자를 추가함으로써 중요한 패턴을 무효화시키고 사기적인 내용을 감지하는 것을 더욱 어렵게 만듭니다.
"Relation camoutflage"에 대해 살펴보겠습니다.
정상적인 리뷰를 제시하거나 신뢰할 만한 사용자와 관계(relation)을 연결함으로써 그들의 프로필을 정당화합니다. [Figure 1]에서 Relation II 하에서 center node는 일반인(benign)과의 연결을 통해 위장하고 있는 것을 확인할 수 있습니다.
○ [Problem]
기존의 방법론들은 이와 같은 그래프(graph)를 그대로 사용하여 GNN aggregation process에 적용하기 때문에 성능 저하를 불러일으킵니다.
○ [Solution]
반면, CAER-GNN은 주어진 그래프(graph)를 그대로 사용하지 않고 center node마다의 이웃을 선별한 후("Neighbor Selector") GNN aggregation process를 사용합니다.
CARE-GNN은 가장 유사한 특성을 가진 $p$개의 이웃을 샘플링 하기 위해 2개의 모듈을 사용합니다.
- Feature camoutflage 문제점을 보완하고자 label-aware similarity measure를 사용합니다(→[Section 2.1]).
- Relation camoutflage 문제점을 보완하고자 relation-aware similarity measure를 사용합니다 (→[Section 2.2]).
2. Proposed Model

▶ Framework
- center node $v_i, {}^{\forall}i$에 대해서 proposed label-aware similarity measure (→[Section 2.1])을 바탕으로 neighbor similarties를 계산합니다.
- 각 relation $\{1,2,3, \cdots, R\}$ 하에서 proposed neighbor selector(→[Section 2.2])를 바탕으로 dissimilar neighbor는 filtering합니다.
- GNN aggregation process(→[Section 2.3])에서
a. 각 relation $\{1,2,3, \cdots, R\}$ 별로 intra-relation aggregation을 사용하여 neighbor embedding을 aggregate합니다.
b. inter-relation aggregation을 통해 서로 다른 relation별 embedding vector를 결합(combine)합니다.
c. 최종적으로 각 노드의 embedding vector가 산출됩니다.
2.1 Label-aware similarity measure
▶ Problem
기존 방법론들은 주어진 그래프(graph)를 그대로 사용함으로써 fraudsters entities와 benign entities의 특성을 서로 비슷하게 학습하기 때문에 GNN aggregation process 과정에서 node embedding vector를 잘못된 방향으로 학습시킵니다.
▶ Solution(or Purpose)
GNN aggregation process에 적용하기 전에 parameterized similarity measure를 사용하여 camouflaged neigbors(fraudsters entities)를 filtering하여 기존의 문제점을 보완합니다.
▶ Parameterized Similarity Measure

$$D^{(l)}(v,v') = ||\sigma(MLP^{(l)}(h_v^{l-1})) - \sigma(MLP^{(l)}(h^{(l-1)}_{v'})||_1, (v,v') \in \varepsilon^{(l-1)}_r \tag{1}$$
$$\text{Similarity Measures}: S^{(l)}(v,v') = 1 - D^{(l)}(v,v') \tag{2}$$
식 $(1)$을 통해 알 수 있듯이 parameterized similarity measure로 one-layer MLP와 $l1$-distance를 사용합니다.
- relation $r$하에서,
one-layer MLP는 학습된 center node $h_v^{l-1}$와 neighbor node $h_{v'}^{l-1}$가 각 label에 속할 확률(probabiltiy)을 산출합니다.- MLP at the $l$-th layer의 입력값: $(l-1)$-th layer의 node embedding vector
- MLP at the $l$-th layer의 산출값: 스칼라 값
- activation function $\sigma$: $\text{tanh}(x) = \dfrac{e^x - e^{-x}}{e^x + e^{-x}}$
- MLP의 산출값을 바탕으로 $l1$-distance를 통해 유사성(similarity)을 계산합니다.
▶ Optimization
손실함수는 식 $(3)$과 같으며 similar measure를 훈련하기 위해 cross-entropy loss를 사용하였습니다.
$$L^{(l)}_{simi} = \sum_{v \in V} - log(y_v \cdot \sigma(\text{MLP}^{(l)}(h^{l}_v))) \tag{3}$$
2.2 Similarity-aware Neighbor Selector

Center node $v$와 neighbor node $v'$의 similarity score $S(v,v')$를 기반으로 dissimilar neighbors(camouflaged neigbors)를 filtering하는 과정입니다(or similar neighbors를 select하는 과정입니다).
▶ Problem
서로 다른 type의 relation $r$ 하에서,
서로 다른 benign entities들은 서로 다른 양만큼의 fradusters와 연결되어 있을 것입니다. 이때 수작업으로 각 node별로 similar neighbor의 수를 지정하는 것은 어렵습니다.
▶ Solution
Reinforcement Learning(RL) 알고리즘을 사용하여 각 relation별로 optimal filtering threshold $p^{(l)}_r \in [0,1]$을 찾아냄으로써 자동으로 similar neighbors의 최적의 수를 고안할 수 있습니다(→[Section 2.2.1], [Section 2.2.2]).
2.2.1 Top-p Sampling
각 relation $r$ 하에서 camouflaged neighbors를 filtering하기 위해 "top-p sampling" 방법을 제안합니다.
Step 1. 계산된 similariy scores $\{ S^{(l)}(v,v')\}, (v,v') \in \varepsilon^{(l)}_r$를 내림차순 정렬합니다
Step 2. 상위 $\color{blue}{p^{(l)}_r \cdot |\{ S^{(l)}(v,v')\}|}$개의 이웃들을 $l$-th layer의 selected neighbors로 선정합니다
Step 3. 그 외의 node들은 모두 제외하기 때문에 GNN aggregation process에 사용되지 않습니다.
[Step 1] ~ [Step 3]은 각 relation $r$별로 진행이 됩니다.
이때 filtering threshold $p^{(l)}_r$을 선정하는데 있어 사용자가 직접 설정할 수 있지만
fraud detection의 경우에는 noise가 존재하기 때문에 각 relation 별로 optimal threshold $p^{(l)}_r$을 찾아야 합니다.
2.2.2 Reinforcement Learning(RL)
CARE-GNN에서는 optimal threshold $p^{(l)}_r$을 reinforcement learning(강화학습)을 통해 찾습니다. 강화학습은 실수(action)와 보상(reward)을 통해 학습을 하여 목표를 찾아가는 알고리즘입니다.
기존의 신경망들이 라벨(정답)이 있는 데이터를 통해서 가중치와 편향을 학습하는 것과 비슷하게 보상(reward)이라는 개념을 사용하여 가중치와 편향을 학습하는 것입니다.
★ Purpose: optimal threshold $p^{(l)}_r \in [0,1]$를 찾는 것.
- $p^{(l)}_r$의 범위가 닫힌 구간(closed interval)이라는 점은 각 relation 하에서 center node의 모든 이웃을 유지할 수도 있고(keep) 모두 버릴 수 있다(discard)는 것을 의미합니다.
초기값 $p^{(l)}_r$이 주어진 상황에서 action과 reward는 다음과 같이 작동합니다.
1. Action
보상(reward)를 기반으로 $p^{(l)}_r$을 어떻게 업데이트 할 지 정합니다.
$$p^{(l)}_r \gets p^{(l)}_r + f(p^{(l)}_r, a^{(l)}_r)^{(e)} \cdot \tau \tag{4}$$
- fixed small value $\tau \in [0,1]$
2. Reward
이전 에포크(epoch)와 현재 에포크(epoch)간의 average distance difference를 기반으로 reward $f(p^{(l)}_r, a^{(l)}_r)$을 계산합니다.
$$G(D^{(l)}_r)^{(e)} = \dfrac{\sum_{v \in V_{train}} D^{(l)}_r(v,v')(e)}{|V_{train}|}$$
$$f(p^{(l)}_r, a^{(l)}_r) ^{(e)} = \begin{cases} +1,& G(D^{(l)}_r)^{(e-1)} - G(D^{(l)}_r)^{(e)} \geq 0
\\
-1, &G(D^{(l)}_r)^{(e-1)} - G(D^{(l)}_r)^{(e)} < 0
\end{cases} \tag{5}$$
현재 epoch $e$에서 새로 선택된 이웃들의 평균 거리가 이전 epoch $e-1$에서 선택된 이웃들의 평균거리보다 작은 경우는 reward $+1$을 줍니다.
반대로, 현재 epoch $e$에서 새로 선택된 이웃들의 평균 거리가 이전 epoch $e-1$에서 선택된 이웃들의 평균거리보다 큰 경우는 reward $-1$을 줍니다.
즉, 우리는 positive reward인 경우는 $p^{(l)}_r$을 증가시키고 그 반대는 감소시킵니다.
2.3 Relation-aware Neighbor Aggregator

Label-aware similarity measure 모듈과 Similarity-aware Neighbor Selector를 통해 각 center node별 dissimilarity neighbor node를 filtering하였습니다.
다음 단계는 neighbor node의 embedding vector를 집계(aggregating)하는 GNN aggregation process입니다.
먼저, intra-relation aggregation을 통해 각 relation별로 이웃을 aggregation한 다음 (→[Section 2.3.1]),
inter-relation aggregation을 통해 서로 다른 relation별 embedding vector를 결합(combine)합니다 (→[Section 2.3.2]).
2.3.1 Intra-relation aggregation
$$h^{(l)}_{v,r} = \text{ReLU}(\text{AGG}^{(l)}_r (\{h^{(l-1)}_v: (v,v') \in \varepsilon^{(l)}_r \})) \tag{5} $$
- $AGG^{(l)}_r$: mean aggreagtion function ${}^{\forall}r$
이웃 노드의 정보를 집계하여 각 relation별 center node $h^{(l)}_{v,r}$을 학습합니다.
만약, relation type이 $3$개인 경우,
각 center node의 $h^{(l)}_{v,1}, h^{(l)}_{v,2}, h^{(l)}_{v,3}$는 각각의 relation 별 이웃 정보를 반영하여 따로 따로 학습이 됩니다.
학습된 $h^{(l)}_{v,1}, h^{(l)}_{v,2}, h^{(l)}_{v,3}$을 하나의 embedding vector $h^{(l)}_v$로 결합(combine)하는 과정이 Inter-relation aggregation입니다.
2.3.2 Inter-relation aggregation
$$h^{(l)}_v = \text{ReLU}(\text{AGG}^{l}_{all} (h^{(l-1)}_v \oplus \{ p^{(l)}_r \cdot h^{(l)}_{v,r}\} | ^{R}_{r=1})) \tag{6}$$
- $h^{(l-1)}_v$: 이전 layer의 tcenter node
- $\color{blue}{h^{(l)}_{v,r}}$: 현재 layer의 the intra-relation neighbor embedding
- $\color{blue}{p^{(l)}_r}$: RL으로부터 학습된 filtering threshold로 inter-relation aggregation weight로 사용됩니다.
- $\oplus$: the emebdding summation operation를 의미합니다.
3. Optimization

각 node $v$의 final embedding vector는 GNN의 마지막 layer이며 이는 $z_v = h^{(L)}_v$라고 지칭하겠습니다.
GNN의 손실함수와 CARE-GNN의 손실함수는 식 $(7)$과 식 $(8)$과 같습니다.
▶ Loss Function of GNN
$$L_{GNN} = \sum_{v \in V} - log(y_v \cdot \sigma(\text{MLP}(z_v)) \tag{7}$$
▶ Loss Function of CARE-GNN
$$L_{CARE} = L_{GNN} + \lambda_1 L^{(1)}_{Simi} + \lambda_2 ||\Theta||_2 \tag{8}$$
- $||\Theta||_2$: 모든 parameter에 대해 the L2-norm
- $\lambda_1, \lambda_2$: weighting parameter
최종 알고리즘은 다음과 같습니다.

본 글에서는 Graph Neural Network(GNN) based Fraud Detection 모델 중 CARE-GNN에 대해서 살펴보았습니다.
실제 데이터로부터 수집된 그래프(graph)를 그대로 사용하지 않고 dissimilarity neighbor node는 filtering 함으로써 GNN aggregation process의 성능을 보다 향상시켰다는 점이 핵심이었습니다.
다음 글에서는 또 다른 그래프 기반 사기 탐지 모델인 GTAN에 대해 살펴보겠습니다.
'Graph(Graph Neural Network)' 카테고리의 다른 글
| [Graph Clustering 방법론] Deep Attentional Embedded Graph Clustering(DAEGC) (0) | 2023.12.23 |
|---|---|
| Scalable MCMC for Mixed Membership Stochastic Blockmodels (0) | 2022.11.21 |
| GCN - Image Classification (0) | 2022.11.03 |
| Bayesian graph convolutional neural networks for semi-supervised classification (0) | 2022.10.09 |
| Semi-Supervised Classification With Graph Convolutional Networks (0) | 2022.09.19 |



