본 글은 논문 [Time-Series Anomaly Detection Service at Microsoft]를 바탕으로 SR-CNN 모델을 설명하고자 합니다.
SR-CNN은 Spectral Residual(SR)과 Convolutional Neural Network(CNN)을 결합한 모델입니다.
▶ [Key Words of SR-CNN]: Anomaly Detection, Time Series, Spectral Reisual(SR)
0. Concept
본 모델에 대해 설명하기에 앞서 본 글 [SR-CNN(1)]에서는 필요한 개념 설명에 대해 먼저 하고자 합니다.
▷ Anomlay Detection & Online Detection
- Anomaly Detection(이상치 탐지)이란, 데이터에서 예상치 못한 사건(unexpected events) 혹은 드문 아이템(rare items)을 발견하는 것을 의미합니다.
- Online Detection이란, 실시간 또는 동적 환경에서 사건 또는 패턴을 감지하는 것을 의미합니다.
Online Detection의 경우, 데이터가 순차적으로 들어올 때 실시간으로 처리되고 판단되는 시스템에 적용되며 짧은 대기시간(low latency) 안에 이상치인지 아닌지 판단하는 것이 중요합니다. SR과 SR-CNN은 시계열 데이터(time-series)에 대한 anomaly detetion 모델이자 online detection 기반에 제안된 모델입니다.
▷ Time Series anomaly detection의 main challenge
Challenge 1. Lack of labels
Anomaly detection을 하기 위해 분포가 계속해서 변하는 수억개의 time-series에 대해 사용자가 동시에 각 time-series에 대해 labeling을 하는 것은 불가능합니다. 즉, supervised model(지도학습모델)로 모델링하기에는 label이 불충분(insufficient)합니다.
Challenge 2. Genearlization
다양한 패턴(ex) seasonal, stable or unstable...)을 갖고 있는 time-series에 대해 잘 작동하는 anomaly detection service가 중요합니다.
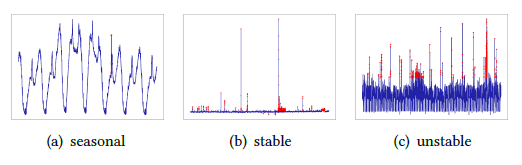
예를 들어, [Figure 1]을 참조하면, 존재하는 방법론 중 'Holt winters'는 (b)와 (c)에 대해서, 'Spot'
은 (a)에 대해서 형편없는 성능을 보여줍니다. 즉, 더 나은 generality solution(일반화 성능)을 갖는 모델이 필요합니다.
Challenge 3. Efficiency
Online detecion의 경우, 수억개의 time-series를 제한된 시간내에 비정상 데이터를 탐지해야 합니다. 그러므로 efficiency는 online anomlay detection service에 있어서 주요한 전제조건입니다.
▷ Fourier Transform(푸리에 변환) & Inverse Fourier Transform(푸리에 역변환)
- Fourier Transform(푸리에 변환)이란, 임의의 입력 신호를 다양한 주파수를 갖는 주기함수(sin, cos)들의 합으로 분해하여 표현하는 것을 의미합니다.
- Period(주기)란, 파동이 한 번 진동하는데 걸리는 시간 또는 길이로 $sin(ws)$의 주기는 $2 \pi / w$입니다.
- Frequency(주파수)란, 1초 동안의 진동횟수로 주기와 서로 역수 관계입니다.
통신 분야에서는 fourier transform을 time domain(시간 도메인)에서 frequency domain(주파수 도메인)으로의 변환, computer vision(컴퓨터 비전) 분야에서는 spatial domain(공간 도메인)에서 frequency domain(주파수 도메인)으로의 변환을 의미합니다. 결국에는 입력신호 $f(x)$을 sine 함수 혹은 cosine 함수로 분해하는 것입니다.
- Inverse Fourier Transform(푸리에 역변환)이란, 푸리에 변환된 결과물로부터 피변환함수를 복원한 것을 의미합니다.
- Inverse Fourier Transform은 원래의 함수로 돌아오는 것으로 이해하면 될 것 같습니다.
"Inverse Fourier Transform(푸리에 역변환)"
$$f(x)=\int^\infty_{-\infty}F(u)e^{j2\pi ux}dx \tag{1}$$
"Fourier Transform(푸리에 변환)"
$$F(u) = \int^{\infty}_{-\infty} f(x) e^{-j2\pi ux}dx \tag{2}$$
- $j=\sqrt{-1}$: 허수단위
- $f(x)$: time domain에서의 원본 입력 신호
- $e^{jw \pi ux}$: frequency가 $u$인 주기함수 성분
- $F(u)$: frequency domain에서의 해당 주기함수 성분의 게수 혹은 강도(amplitude)
식 $(1)$은 inverse fourier transform으로 함수 $f$를 모든 가능한 주파수 $u$의 주기함수 $e^{j2\pi ux}$들의 일차결합입니다.
※ Reference(참조)
Question: $e^{j2\pi ux}$는 왜 주기함수인가?
Answer: 오일러 공식에 의해 설명가능합니다.
[오일러 공식]: $e^{j \theta} = cos \theta + j sin \theta$
오일러 공식에 의해 $e^{j2 \pi ux} = cos(2 \pi ux) + j sin(2 \pi ux)$가 성립합니다. $cos(2 \pi ux),sin(2 \pi ux)$는 period가 $1/u$, frequency가 $u$인 주기함수입니다. 즉, $e^{j 2\pi ux}$는 주파수가 $u$인 정현파(sinusoidal wave: 파형이 sine 함수 혹은 cosine 함수인 파동)입니다.
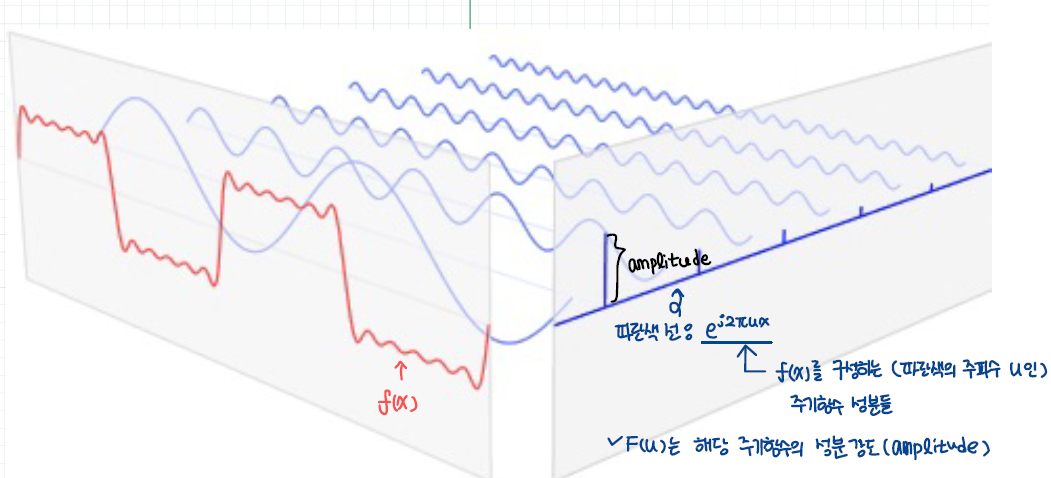

[Figure 2]를 참조하면 빨간색 선(red line)이 time domain에서의 입력 신호 $f(x)$, 파란색 선(blue line)이 $e^{j2\pi ux} = cos(2 \pi ux) + j sin(2 \pi ux)$로 입력 신호 $f(x)$를 구성하는 주파수가 $u$인 주기함수 성분들입니다. $F(u)$는 해당 주기함수의 성분 강도(amplitude)로 [Figure 2]를 통해 식 $(1)$을 이해할 수 있습니다.
→ 식 $(1)$: 각 주기함수 $e^{j2\pi ux}$와 해당 주기함수의 성분 강도 $F(u)$의 곱의 일차결합(적분) $f(x)$.
▷ Amplitude Spectrum & Phase Spectrum
식 $(2)$는 실수부(Real)과 허수부(Imaginary)의 합의 형태인 복소수 $\color{blue}{F(u) = R(u) + jI(u)}$로 표현 가능합니다.


"Amplitude Spectrum"
$$|F(u)| = [R^2(u)+I^2(u)]^{1/2}$$
Amplitude specturm $|F(u)|$은 시간에 대한 함수 $f(x)$를 fourier transform $F(u)$ 했을 때 얻어지는 복소함수에서 각 주파수에서의 진폭을 의미하며 원래 함수를 구성하던 그 주파수 성분의 크기입니다.
※ [Figure 3]의 왼쪽 그림
"Phase Specturm"
$$\phi(u) = tan^{-1}[\dfrac{I(u)}{R(u)}]$$
Phase spectrum은 편각으로 기본 sine 곡선과의 위상차를 나타냅니다.
※ [Figure 3]의 오른쪽 그림
본 글 [SR-CNN(1)]에서는 Anomaly detection 및 Online detecion에 대한 정의와 Fourier Transform(푸리에 변환)에 대해 살펴보았습니다. 본 글의 내용을 토대로 다음 글 [SR-CNN(2)]에서 "Spectral Residual(SR)"과 "SR-CNN"에 대해 본격적으로 살펴보고자 합니다.



