Wrapper는 variable selection 방법 중 하나로 반복되는 알고리즘을 사용하는 지도 학습 기반의 축소 알고리즘이다.
Wrapper에는 forward selection, backward elimination, stepwise selection, genetic algorithm이 존재한다.
1. Exhaustive Search(ES)
Exhaustive Search(ES, 완전탐색)는 variable selection 중 가장 단순한 방식이다. 예를 들어, $x1, x2, x3$ 데이터가 존재하는 경우, ES 방법을 사용하면 다음과 같이 가능한 모든 조합을 찾는다.
$$f(x_1), f(x_2), f(x_3) $$
$$f(x_1, x_2), f(x_1, x_3), f(x_2, x_3)$$
$$f(x_1, x_2, x_3)$$
위의 조합 중 성능이 가장 좋은 것을 고른다. 성능을 판단하는 기준에는 AIC, BIC, Adjusted $R^2$, Mallow's Cp가 있다. 이처럼 ES 방법은 모든 가능한 조합을 고려하기 때문에 global optimum(전역 최적점)을 찾을 수 있다. 즉, local optimum(지역 최적점)에 빠질 우려가 없다. 하지만 ES 방법을 사용하면 데이터셋의 변수가 n개 일 때, $2^n-1$만큼의 모델을 평가해야 한다. n의 개수가 아주 큰 경우, 현실적으로 사용 불가능하다. 이에 대한 방안으로 Forward Selection과 Backward Elimination을 제시한다. 두 방법은 ES만큼의 성능은 아니지만 어느 정도 성능을 유지하면서 ES에서 걸리는 시간을 줄인 방법이다.
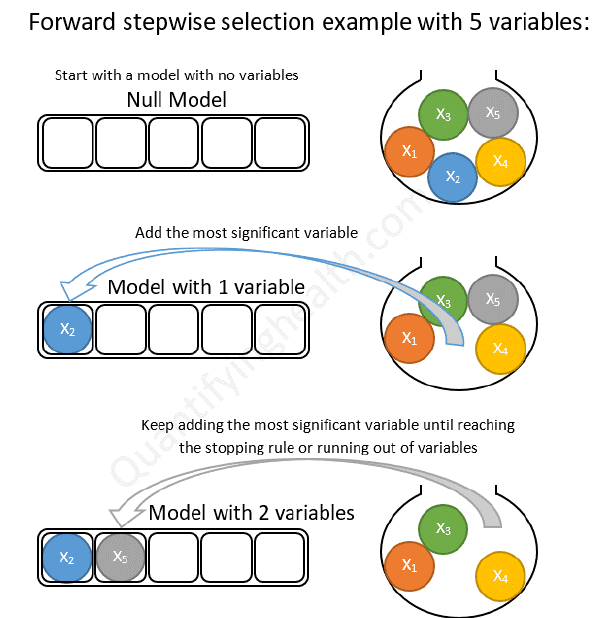
2. Forward Selection(전진선택법)
Forward Selection(전진선택법)은 가장 유의미한 변수를 선택해 나가는 방식으로 변수가 없는 상태부터 시작해서 변수를 하나씩 늘려나가는 방향으로 나아간다. 이전의 단계에서 성능의 향상이 없을 때까지 새로운 변수를 계속해서 추가해준다.
예를 들어, 5개의 변수가 존재한다고 가정해본다($X = (x_1, x_2, x_3, x_4, x_5) \in R^5$).
$$y = \beta_0 + \beta_1x_1+\beta_2x_2+\beta_3x_3+\beta_4x_4+\beta_5x_5$$모델은 다중회귀모델이며 성능을 판단하는 기준은 adjusted $R^2$이라고 해본다.
먼저, 변수 하나만 선택하여 성능을 비교해본다.
$$\hat{y} = \beta_0+\beta_1x_1, \, R^2_{adj} = 0.48$$
$$\hat{y} = \beta_0+\beta_2x_2, \, R^2_{adj} = 0.56$$
$$\hat{y} = \beta_0+\beta_3x_3, \, R^2_{adj} = 0.51$$
$$\hat{y} = \beta_0+\beta_4x_4, \, R^2_{adj} = 0.38$$
$$\hat{y} = \beta_0+\beta_5x_5, \, R^2_{adj} = 0.32$$
두 번째 모델의 성능이 가장 좋으므로 변수 $x_2$를 선택한다. 이제 변수 $x_2$가 존재하는 상황에서 새로운 변수를 하나씩 추가해준다.
$$\hat{y} = \beta_0+\beta_2x_2+\beta_1x_1, \, R^2_{adj} = 0.60$$
$$\hat{y} = \beta_0+\beta_2x_2+\beta_3x_3, \, R^2_{adj} = 0.64$$
$$\hat{y} = \beta_0+\beta_2x_2+\beta_4x_4, \, R^2_{adj}= 0.78$$
$$\hat{y} = \beta_0+\beta_2x_2+\beta_5x_5, \, R^2_{adj} = 0.78$$
세 번째 모델의 성능이 가장 좋으며 이전의 단계에서보다 성능이 향상되었으므로 변수 $(x_2, x_5)$를 선택한다. 이제 변수 $(x_2, x_5)$가 존재하는 상황에서 새로운 변수를 하나씩 추가해준다.
$$\hat{y} = \beta_0+\beta_2x_2+\beta_5x_5 + \beta_1x_1, \, R^2_{adj} = 0.70$$
$$\hat{y} = \beta_0+\beta_2x_2+\beta_5x_5 + \beta_3x_3, \, R^2_{adj} = 0.74$$
$$\hat{y} = \beta_0+\beta_2x_2+\beta_5x_5 + \beta_4x_4, \, R^2_{adj} = 0.68$$
두 번째 모델의 성능이 가장 좋지만 이전 단계에서 성능 향상이 이루어지지 않은 것을 확인할 수 있다.
따라서, Forward selection을 통해 최종적으로 선택된 변수 집합은 $(x_2, x_5)$이다. Forward Selection의 큰 특징 중 하나는 변수가 한 번 추가되면 절대적으로 제거될 수 없다.
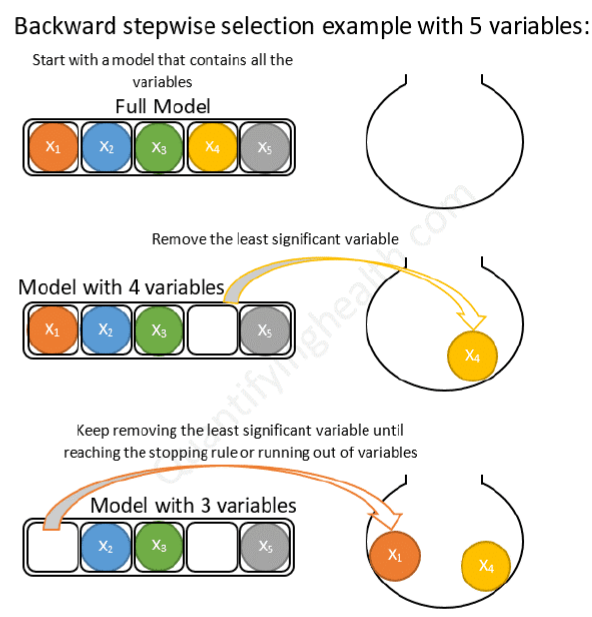
3. Backward Elimination
Backward Elimination(후진제거법)은 무의미한 변수를 제거해 나가는 방식이다. 모든 변수를 가진 모델에서 시작하여 특성을 하나씩 줄여나가기 때문에 모델의 성능이 저하될 수밖에 없다. 특정 변수를 제거한 경우, 성능 저하가 미미한 경우 변수를 제외시킨다. Backward Elimination 방법도 가장 큰 특징이 한 번 제거된 변수도 절대적으로 다시 선택될 수 없다.
이번에도 마찬가지로 5개의 변수가 존재한다고 가정해본다($X = (x_1, x_2, x_3, x_4, x_5) \in R^5$).
$$y = \beta_0 + \beta_1x_1+\beta_2x_2+\beta_3x_3+\beta_4x_4+\beta_5x_5$$
모델은 다중회귀모델이며 성능을 판단하는 기준은 $adjusted \, R^2$이다.
$$y = \beta_0 + \beta_1x_1+\beta_2x_2+\beta_3x_3+\beta_4x_4+\beta_5x_5, \, R^2_{adj} = 0.77$$
$$y = \beta_0 +\beta_2x_2+\beta_3x_3+\beta_4x_4+\beta_5x_5, \, R^2_{adj}= 0.77$$
$$y = \beta_0 + \beta_1x_1+\beta_3x_3+\beta_4x_4+\beta_5x_5, \, R^2_{adj} = 0.65$$
$$y = \beta_0 + \beta_1x_1+\beta_2x_2+\beta_4x_4+\beta_5x_5, \, R^2_{adj} = 0.77$$
$$y = \beta_0 + \beta_1x_1+\beta_2x_2+\beta_3x_3+\beta_5x_5, \, R^2_{adj}= 0.62$$
$$y = \beta_0 + \beta_1x_1+\beta_2x_2+\beta_3x_3+\beta_4x_4, \, R^2_{adj}= 0.73$$
변수 $x_3$을 제거한 경우, 모델의 성능 변화가 없다는 것을 알 수 있다. 즉, $x_3$은 모형을 만드는데 무의미한 변수이며 제거 해도 상관없다. 이제 변수 $x_3$이 제거된 상황에서 변수를 하나씩 제거해 본 결과 다음과 같다.
$$y = \beta_0 + \beta_1x_1+\beta_2x_2+\beta_4x_4+\beta_5x_5, \, R^2_{adj}= 0.77$$
$$y = \beta_0 + \beta_2x_2+\beta_4x_4+\beta_5x_5, \, R^2_{adj} = 0.76$$
$$y = \beta_0 + \beta_1x_1+\beta_4x_4+\beta_5x_5, \, R^2_{adj} = 0.63$$
$$y = \beta_0 + \beta_1x_1+\beta_2x_2+\beta_5x_5, \, R^2_{adj} = 0.70$$
$$y = \beta_0 + \beta_1x_1+\beta_2x_2+\beta_4x_4, \, R^2_{adj} = 0.68$$
변수 $x_1$을 제거한 경우, 모델의 성능 변화가 미미하게 저하된 것을 알 수 있다. 즉, BE 방법을 통해 변수 $(x_1,x_3)$은 모형을 만드는데 무의미한 변수로 판단됨을 알 수 있다.
$$y = \beta_0 + \beta_2x_2+\beta_4x_4+\beta_5x_5, \, R^2_{adj} = 0.76$$
$$y = \beta_0 + \beta_4x_4+\beta_5x_5, \, R^2_{adj} = 0.60$$
$$y = \beta_0 + \beta_2x_2+\beta_5x_5, \, R^2_{adj} = 0.56$$
$$y = \beta_0 + \beta_2x_2+\beta_4x_4, \, R^2_{adj} = 0.65$$
변수를 또 제거한 경우, 급격한 성능 저하가 발생된 것을 확인할 수 있다. 따라서, BE 방법을 통해 최종적으로 제거된 변수는 $(x_1, x_3)$이다.
4. Stepwise Selection
앞서 말했듯이, FS의 경우 한 번 선택된 특성은 제거되지 않고, BE는 한 번 제거된 특성은 다시 선택되지 않는다. 두 방법 모두 더 많은 특성 조합에 대해 모델을 평가할 수 없다는 단점이 존재한다. 이에 대해 성능을 FS/BE보다 높이는 대신 소요 시간도 늘리는 방안인 Stepwise Selection을 제시한다. Stepwise Selection은 Foward Selection과 Backward Elimination을 매 단계마다 반복적으로 적용하는 방식이다. Stepwise Selection은 두 가지 방법과 달리 선택된 변수도 다시 제거될 수 있으며 마찬가지로 제거된 변수도 다시 선택될 수 있다. 예시를 들어 설명해 보고자 한다.
아무런 변수가 존재하지 않은 상황에서 FS 방법을 시행한다.
$$\hat{y} = \beta_0+\beta_1x_1, \, R^2_{adj} = 0.48$$
$$\hat{y} = \beta_0+\beta_2x_2, \, R^2_{adj}= 0.56$$
$$\hat{y} = \beta_0+\beta_3x_3, \, R^2_{adj} = 0.51$$
$$\hat{y} = \beta_0+\beta_4x_4, \, R^2_{adj} = 0.38$$
$$\hat{y} = \beta_0+\beta_5x_5, \, R^2_{adj} = 0.32$$
성능이 가장 좋은 두 번째 모델을 선택한다. 선택된 모델에 대해 제거할 변수가 존재하지 않으므로 BE 방법을 사용하지 않고 다시 FS 방법을 수행한다.
$$\hat{y} = \beta_0+\beta_2x_2+\beta_1x_1, \, R^2_{adj} = 0.60$$
$$\hat{y} = \beta_0+\beta_2x_2+\beta_3x_3, \, R^2_{adj} = 0.58$$
$$\hat{y} = \beta_0+\beta_2x_2+\beta_4x_4, \, R^2_{adj} = 0.70$$
$$\hat{y} = \beta_0+\beta_2x_2+\beta_5x_5, \, R^2_{adj} = 0.68$$
성능이 가장 좋은 세 번째 모델을 선택한다. 이 모델에 BE를 수행하면 다시 $\hat{y}=\beta_0+\beta_3x3$이므로 제대로 적용되지 않는다. 따라서, 다시 FS를 수행한다.
$$\hat{y} = \beta_0+\beta_2x_2+\beta_4x_4+\beta_1x_1, \, R^2_{adj} = 0.75$$
$$\hat{y} = \beta_0+\beta_2x_2+\beta_4x_4+\beta_3x_3, \, R^2_{adj} = 0.68$$
$$\hat{y} = \beta_0+\beta_2x_2+\beta_4x_4+\beta_5x_5, \, R^2_{adj} = 0.77$$
성능이 가장 좋은 세 번째 모델을 선택한다. 이 단계부터는 이제 BE가 적용된다. BE를 적용한 결과 다음과 같다.
$$\hat{y} = \beta_0+\beta_2x_2+\beta_4x_4, \, R^2_{adj} = 0.74$$
$$\hat{y} = \beta_0+\beta_2x_2+\beta_5x_5, \, R^2_{adj} = 0.76$$
$$\hat{y} = \beta_0+\beta_4x_4+\beta_5x_5, \, R^2_{adj} = 0.80$$
성능이 가장 좋은 모델인 세 번째 모델이 선택된다. 이와 같은 과정을 어떤 변수도 선택이 안 되고 제거도 안 될 때까지 반복한다.
[Stepwise Selection Algorithm]
- Start with model with no predictors.
- Add variable with largest F-statistic (provided P less than some cut-off)
- Refit with this variable added. Recompute all F statistics for adding one of the remaining variables and add variable with largest F statistic.
- At each step after adding a variable try to eliminate any variable not significant at some level (that is, do BACKWARD elimination till that stops)
- After doing the backwards steps take another FORWARD step.
- Continue until every remaining variable is significant at cut-off level and every excluded variable is insignificant OR until variable to be added is same as last deleted variable.
참고자료: https://www.youtube.com/playlist?list=PLetSlH8YjIfWMdw9AuLR5ybkVvGcoG2EW
'Machine Learning > Dimensionality Reduction' 카테고리의 다른 글
| t-SNE (0) | 2023.01.02 |
|---|---|
| Local Linear Embedding(LLE) (0) | 2023.01.02 |
| ISOMAP (0) | 2023.01.01 |
| Principal Component(PCA) & Multidimensional Scaling(MDS,다차원 척도법) (0) | 2022.12.22 |
| Dimensionaltiy Reduction의 필요성(차원축소 필요성) (0) | 2022.12.21 |



