ISOMAP은 다차원 스케일링(MDS) 또는 주성분 분석(PCA)의 확장이자 두 방법론을 결합한 방법론으로 볼 수있다. PCA와 MDS는 선형변환을 통해 차원을 축소하는 반면, ISOMAP은 비선형 변환을 통한 차원 축소 기법이다.

Figure 1에서 두 점은 유클리디안 거리로는 가깝지만 실제로는 색깔이 나타내는 의미만큼 멀리 떨어져 위치함을 알 수 있다. 선형 변화 기법인 MDS와 PCA를 바로 적용하는 경우, 3차원에서 갖는 최단거리를 이용하여 부적합하다.반면, Isomap 알고리즘은 그래프 공간 상에서 두 노드간 최단거리를 갖는 알고리즘을 적용하며 두 데이터간의 실제 특징을 반영하는 거리 정보를 사용하는데 효과적인 차원 축소를 추구한다.핵심은 매니폴드 상에서 두 점 사이의 실제 도달 거리를 구하는 것이다.
1. 인접한 이웃 그래프 구축(Graph 형성)
첫번째 단계에서는 어떤 점들이 매니폴드(manifold) 상에서 서로 가까이 위치하는가를 측정한다.

Graph는 node와 edge로 구성된다. node는 각 점이며 node 간의 연결여부 집합인 edge set을 추정하는데 대표적으로 두 가지 방식이 존재한다.
(1). $\epsilon$ isomap : 고정된 기준값인 $\epsilon$을 기준으로 그보다 거리가 가까운 경우의 모든 두 점을 서로 연결한다.
(2). $K$-isomap : 자기 자신과 가장 가까운 k개의 점을 연결하는 KNN방식으로 모든 점들을 서로 연결한다.
실질적으로 가장 짧은 거리를 구해야하므로 위의 두 가지 방법 모두 전체 데이터가 하나라도 고립되어 있거나 끊겨져 있으면 안 된다.
2. 두 점 간의 최단 경로 그래프 계산
- 두 점 $i$와 $j$에 대하여 두 점이 서로 연결되어 있는 경우, $d_G(i,j)=d_X(i,j)$
- 두 점 $i$와 $j$에 대하여 두 점이 서로 연결되어 있지 않은 경우, $d_G(i,j)=\infty$
- 그 후, 1부터 N개까지의 k개 있어서 점 i와 j간의 최단거리를 의미하는 $d_G(i,j)=min(d_G(i,j),d_G(i,k)+d_G(k,j)$
두 점간의 최단 경로 그래프를 계산하는데 대표적으로 사용되는 알고리즘은 Dijkstra 알고리즘과 Floyd's 알고리즘이 존재한다. 두 알고리즘에 대한 내용은 '이것이 취업을 위한 코딩 테스트다 with 파이썬'을 참고해 정리하였다.
2.1 Dijkstra 알고리즘
최단 경로 문제는 보통 그래프를 이용해서 표현된다.

Figure 3을 보면, 각 지점은 노드를 의미하며 지점 간 연결된 선은 간선(vertex)를 의미한다. 그래프는 방향성이 있거나 없는 경우로 구분할 수 있는데(directed graph vs. undirected graph), 방향성이 있는 경우에 대한 두 노드 간의 최단 경로를 찾는 과정을 설명해 보고자 한다.
1번 노드에서 다른 모든 노드(2번, 3번, 4번, 5번, 6번)로 가는 최단 경로를 설정하는 문제이다.
[Step 1]
초기 상태에서 1번 노드를 제외하고 다른 모든 노드로 가는 최단 거리는 '무한'으로 초기화시킨다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | 0 | 무한 | 무한 | 무한 | 무한 | 무한 |
먼저, 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 1번 노드를 선택한다. 출발 노드에서 출발 노드의 거리는 0으로 보기 때문에 처음에는 출발 노드가 선택된다. (visitied node = ['node 1'])
[Step 2]

1번 노드에서 갈 수 있는 노드는 2번, 3번, 4번이다. 1번 노드를 거쳐서 2번, 3번, 4번 노드로 가는 최소 비용은 2(0+2), 5(0+5), 1(0+1)이다. 현재 2번, 3번, 4번 노드로 가는 비용이 '무한'으로 설정되어 있기 때문에 더 짧은 경로를 찾았으므로 새로운 값으로 갱신한다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | 0 | 2 | 5 | 1 | 무한 | 무한 |
[Step 3]

지금까지 방문한 노드(visited node)는 1번 노드이다. 마찬가지로 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드인 4번 노드를 선택한다(visited node’ : [node 1, node 4]). 4번 노드에서 갈 수 있는 노드는 3번과 5번 노드이다. 4번 노드를 거쳐서 3번, 5번 노드로 가는 최소 비용은 4(1+3), 2(1+1)이다. 이 두 값은 현재 설정된 값보다 작으므로 갱신시켜준다.
| 노드 번호 | 1 | 3 | 4 | 5 | 6 | |
| 거리 | 0 | 2 | 4 | 1 | 2 | 무한 |
[Step 4]

지금까지 방문한 노드는 1번과 4번이며 지금까지 방문하지 않는 노드 중에서 최단거리가 가장 짧은 노드는 2번과 5번이다. 이런 경우, 일반적으로 번호가 작은 노드를 선택한다('visited node’ : [node 1, node 2, node 4]). 2번 노드에서 갈 수 있는 노드는 3번과 4번이다. 2번 노드를 거쳐서 3번, 4번 노드로 가는 최소 비용은 5(2+3), 3(2+1)이다. 현재 설정된 값보다 크므로 갱신되지 않는다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | 0 | 2 | 3 | 1 | 2 | 4 |
[Step 5]

지금까지 방문한 노드는 1번, 4번, 2번이며 이번에는 5번 노드가 선택된다(’visited node’ : [node 1, node 4, node 2, node 5]). 5번에서 갈 수 있는 노드는 3번과 6번이다. 5번 노드를 거쳐서 3번, 6번 노드로 가는 최소 비용은 3(1+1+1), 4(1+1+2)이다. 현재 설정된 값보다 작으므로 갱신된다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | 0 | 2 | 3 | 1 | 2 | 4 |
[Step 6]

지금까지 방문한 노드는 1번→4번→2번→5번이며(’visited node’ : [node 1, node 4, node 2, node 5]) 지금까지 방문하지 않는 노드 중 가장 짧은 노드인 3번 노드가 선택된다. 3번 노드에서 갈 수 있는 노드는 2번과 6번이다. 3번 노드를 거쳐서 2번과 6번 노드로 가는 최소 비용은 6(1+1+1+3), 8(1+1+1+5)이다. 현재 설정된 값보다 크므로 갱신되지 않는다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | 0 | 2 | 3 | 1 | 2 | 4 |
[Step 7]

마지막으로 6번 노드를 선택한다. 6번 노드에서 갈 수 있는 노드는 없으며 지금까지의 최종 최단 거리는 다음과 같다.
| 노드 번호 | 1 | 2 | 3 | 4 | 5 | 6 |
| 거리 | 0 | 2 | 3 | 1 | 2 | 4 |
최종 최단 거리 결과를 보면 1번 노드에서 출발해서 2번, 3번, 4번, 5번, 6번 노드까지 가기 위한 최단 경로는 2, 3, 1, 2, 4이다. 다익스트라 최단 경로 알고리즘은 '방문하지 않은 노드 중에서 가장 최단 거리가 짧은 노드를 선택'하는 과정을 반복한다. 앞선 예시를 보면, 한 번 선택된 노드는 최단 거리가 더 이상 줄어들지 않는다. 2번째로 선택된(방문한) 4번 노드를 보면, 선택된 이후 최단 거리가 감소되지 않았던 것을 확인할 수 있다. 즉, 다익스트라 알고리즘이 진행되면서 한단계당 하나의 노드에 대한 최단 거리를 확실히 찾는 것이다. 따라서, 마지막 선택되는 노드에 대해서는 해당 노드를 거쳐 다른 노드로 가는 경우를 굳이 확인할 필요가 없다.
관련 코드를 살펴보면 다음과 같다.
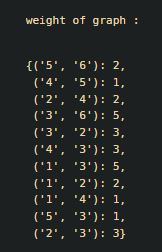
Graph에서 edge와 weight는 dictionary로 표현하며 edges는 자신의 인접한 노드들로 표현하므로 list 값으로 하여 연결된 노드들을 넣는다. weight(distance)는 두 개의 노드 사이의 weight(distance)이므로 tuple(node, another_node)를 키(key)로 하고, 가중치를 값(value)으로 한다.
from collections import defaultdict
class Graph():
def __init__(self):
self.edges = defaultdict(list)
self.weights = {}
def add_edge(self, from_node, to_node, weight):
# Note: assumes edges are bi-directional
self.edges[from_node].append(to_node)
self.weights[(from_node, to_node)] = weight
self.weights[(to_node, from_node)] = weightedges = {
('1','2',2),
('1','3',5),
('1','4',1),
('2','3',3),
('2','4',2),
('3','2',3),
('3','6',5),
('4','3',3),
('4','5',1),
('5','3',1),
('5','6',2)
}
graph = Graph()
for edge in edges:
graph.add_edge(*edge)
print("edge of graph: ", graph.edges)
print("weight of graph: ", graph.weights)
def dijsktra(graph, initial, end):
shortest_paths = {initial: (None, 0)}
current_node = initial # 시작점 노드를 현재 노드로 추가한다.
visited = set() # 방문한 노드들을 추가한다.
while current_node != end:
visited.add(current_node) # 현재 노드를 방문한다.
destinations = graph.edges[current_node] # 인접한 노드를 살펴본다.
weight_to_current_node = shortest_paths[current_node][1] # 현재 방문 중인 노드의 weight
print("neighbors of", current_node, "current_node",destinations)
for next_node in destinations: # 인접한 노드 모두를 살펴본다.
# 현재 노드(current_node)와 인접한 노드(next_node)가 연결된 edge의 weight + 현재 weight
weight = graph.weights[(current_node, next_node)] + weight_to_current_node
print(current_node, next_node, "weight", weight)
if next_node not in shortest_paths: # shortest path에 없다면 현재를 추가한다.
shortest_paths[next_node] = (current_node, weight)
else: # 현재 shortest path에 있다면
current_shortest_weight = shortest_paths[next_node][1]
if current_shortest_weight > weight: # 현재 weight가 적다면 업데이트 한다.
shortest_paths[next_node] = (current_node, weight)
# 다음으로 이동할 node는 shortest path에서 아직 방문하지 않은 node로 이동한다.
next_destinations = {node: shortest_paths[node] for node in shortest_paths if node not in visited}
if not next_destinations:
return "Route Not Possible"
# weight가 가장 적은 노드로 이동한다.
current_node = min(next_destinations, key=lambda k: next_destinations[k][1])
destination_node = current_node # 현재 current_node는 destination node이다.
# destination에서 source로 이동하면서 node를 추가한다.
path = []
while destination_node is not None: # 시작 노드로 올 때 까지 반복한다.
path.append(destination_node)
next_node = shortest_paths[destination_node][0] # 다음 노드를 고른다.
print("next", next_node)
destination_node = next_node # destination_node를 다음 노드로 설정하면서
path = path[::-1] # 리스트를 반대로 정렬한다.
return pathdijsktra(graph,'1','6')
1번 노드에서 6번 노드로 가는 최단 경로는 위에서 살펴본 것과 같이 [node 1 -> node 4 -> node 5 -> node 6]이다.
2.2 Floyd's 알고리즘
다익스트라 알고리즘은 '한 지점에서 다른 특정 지점까지의 최단 경로를 구해야 하는 경우'에 사용할 수 있는 최단 경로 알고리즘이다. 반면, 플로이드 워셜 알고리즘은 '모든 지점에서 다른 모든 지점까지의 최단 경로'를 모두 구해야 하는 경우'에 사용할 수 있는 알고리즘이다.
[다익스트라 알고리즘 vs. 플로이드 알고리즘]
<다익스트라 알고리즘>
- 단계마다 최단 거리를 가지는 노드를 하나씩 반복적으로 선택.
- 해당 노드를 거쳐 가는 경로를 확인하며, 방문하지 않는 노드 중에서 최단 거리를 갖는 노드를 찾아 최단 거리 테이블을 갱신하는 방식으로 동작.
- 출발 노드가 1개이므로 다른 모든 노드까지의 최단 거리를 저장하기 위해 1차원 리스트 이용.
- 그리디 알고리즘
<플로이드 알고리즘>
- 다익스트라 알고리즘과 마찬가지로 단계마다 ‘거쳐 가는 노드’를 기준으로 알고리즘을 수행.
- 다익스트라 알고리즘과 달리, 매번 방문하지 않는 노드 중에서 최단 거리를 갖는 노드를 찾을 필요가 없음.
- 노드의 개수 = N개일 때, 알고리즘 상으로 N번의 단계를 수행하며, 단계마다 $O(N^2)$의 연산을 통해 ‘현재 노드를 거쳐 가는’ 모든 경로를 고려. 따라서, 플로이드 위셜 알고리즘의 총시간 복잡도는 $O(N^3)$.
- 모든 노드에 대하여 다른 모든 노드로 가는 최단 거리 정보를 담아야 하기 때문에 2차원 리스트를 처리해야 함. 즉, N번의 단계에서 매번 $O(N^2)$의 시간이 소요됨.
- 다이나믹 프로그래밍
플로이드 알고리즘은 각 단계에서 해당 노드를 고쳐가는 경우를 고려한다. 예를 들어서, 현재 노드가 1번 노드인 경우, 1번 도르를 중간에 거쳐 지나가는 경우를 모두 고려하면 된다(A번 노드 -> 1번 노드 -> B번 노드). 현재 최단 거리 테이블에 A번 노드에서 B번 노드로 이동하는 비용이 3으로 기록되어 있는 경우, A번 노드 -> 1번 노드 -> B번 노드로 이동하는 비용이 2라는 것이 밝혀지면, A번 노드에서 B번 노드로 이동하는 비용이 2로 갱신된다. 즉, 알고리즘에서는 현재 확인하고 있는 노드(예시에서는 1번 노드)를 제외하고, (N-1)개의 노드 중에서 서로 다른 노드 (A,B) 쌍을 선택하며 이후에 A번 노드 → 1번 노드 → B로 가는 비용을 확인한 뒤에 최단 거리를 갱신한다. $_{N-1}P_2$개의 쌍을 단계마다 반복해서 확인하면 된다. $O(_{N-1}P_2 \approx O(N^2)$, 전체 시간 복잡도는 $O(N^3)$으로 볼 수 있다.
3. MDS 방법론을 사용하여 d차원 임베딩 구축
ISOMAP 알고리즘에 대해 다시 정리해보면,
- Step 01: Graph 형성 ($\epsilon$ isomap & $K$ isomap)
- Step 02: 두 점(노드)간의 최단 경로 찾기(Dijkstra 알고리즘 & Floyd's 알고리즘)
- Step 03: MDS 방법론을 사용하여 d-차원 임베딩 구축
그래프를 형성하고, 그래프를 이용해서 distance matrix를 만들고 MDS를 적용하는 것이 ISOMAP의 과정이다.
참고자료
https://www.youtube.com/playlist?list=PLetSlH8YjIfWMdw9AuLR5ybkVvGcoG2EW
https://woosikyang.github.io/first-post.html
https://product.kyobobook.co.kr/detail/S000001810273?utm_source=google&utm_medium=cpc&utm_campaign=googleSearch&gclid=CjwKCAiA-8SdBhBGEiwAWdgtcP2XrdjDhDUI4uEe0M9BmYWMV47LjEjEykujmhVOUf1T01Q6lsyQphoCIUQQAvD_BwE
'Machine Learning > Dimensionality Reduction' 카테고리의 다른 글
| t-SNE (0) | 2023.01.02 |
|---|---|
| Local Linear Embedding(LLE) (0) | 2023.01.02 |
| Principal Component(PCA) & Multidimensional Scaling(MDS,다차원 척도법) (0) | 2022.12.22 |
| Supervised Selection - Forward/Backward/Stepwise (0) | 2022.12.21 |
| Dimensionaltiy Reduction의 필요성(차원축소 필요성) (0) | 2022.12.21 |



