Principal Component(PCA)와 Multidimensional Scaling(MDS)는 unsupervised dimensionality Reduction 방법 중 하나로 선형변환을 통해 차원축소를 하는 기법이다. PCA는 객체가 가진 분산의 정보를 이용하고 MDS는 객체 간의 거리에 대한 정보를 기반으로 차원축소를 한다.
1. Principal Component(PCA)
1.1 Definitioin
PCA는 principal component라고 불리는 새로운 변수 집합을 통해 다변량 고차원의 데이터로부터 중요한 정보를 추출한다. PCA의 주관심은 covariance matrix($\sum$)이며 PCA가 보존하고자 하는 데이터의 특성도 covariance matrix($\sum$)이다. Principal Component(PC)는 p개의 random variable($X_1, X_2, ..., X_p$)의 선형결합(linear combination)의 형태이다. PC의 수는 기존의 변수의 수보다 적거나 같다.

1.2 Purpose
PCA는변수들의 선형결합을 통해 변수들의 분산-공분산 구조를 설명한다. PCA는 가장 큰 분산이 가진 방향성이 가장 중요한 정보를 보유하고 있다고 가정하며 PCA의 목적은 데이터의 분산이 최대가 되는 방향을 찾는 것이다. 즉, 전체 데이터로 볼 때 정보량이 많지 않는 벡터를 제외시키며 기존의 데이터 분산을 최댛나 보존하는 직교 기저(base)를 찾는 것이다.
결과적으로, PCA는 고차원의 다변량 데이터를 시각화가 가능하며 기존의 정보를 최대한 보존한 2차원 혹은 3차원 데이터로 선형변환하는 기법이다.
- $X_1, X_2,...,.X_p$: Original Variables
- $a_i =[a_{i1},..,a_{ip}]: i^{th}$ basis or principal component
- $Y_1,Y_2,...,Y_p$ : Variables after the projection onto the basis
- $Y_1 = a^t_1X = a_{11}X_1+a_{12}X_2+...+a_{1p}X_p$
- $Y_2 = a^t_2X = a_{21}X_1+a_{22}X_2+...+a_{2p}X_p$
- ....
- $Y_p = a^t_1X = a_{p1}X_1+a_{p2}X_2+...+a_{pp}X_p$
첫번째 principal component는 모든 unit vector a 사이에서 maximum variance(최대 분산)을 가진 선형 결합($a_1^tx$)이다. 첫번째 principal component와 두번째 principal component는 서로 상관되어 있지 않다. ↔ $Cov(a_1^tx,a_2^tx)=0$

위의 그림을 보면, PC1은 가장 큰 분산을 가진 first principal direction이며 PC2는 두번째로 큰 분산을 가진 second most important direction이다. 또한, PC1과 PC2는 서로 orthogonal(직교)한 것도 알 수 있다.
1.3 Procedure of PCA
[Step 1]. Data Centering
변수들의 평균을 0으로 만들어준다.
[Step 2]. Formulate the Optimization Problem
만약 vector $x$가 basis $\alpha$에 사영되었다고 가정하면, $y=a^tx$의 분산은 다음과 같다.
$$Var(y) = Var(a^tx) \dfrac{1}{n}(a^TX)(a^TX)^T = \dfrac{1}{n}a^TXX^Ta=a^TSa, XX^T = \sum, \, \dfrac{1}{n}XX^T=\dfrac{1}{n}\sum=S$$
S는 sample covariance matrix이다.(x는 normalized variable이다.) PCA의 목적은 $var(y)=var(a^tx)$를 최대화하는 것이다.
$$maxa^TSa ↔ argmax_{a}a^TSa$, s.t. $a^Ta = 1......(1)$$
[Step 3]. Obtain the Solution
Lagrangian multiplier에 따라, (1)의 식은 다음과 같이 변형된다.
$$L = a^TSa- \lambda(a^Ta-1)$$
$$\dfrac{\partial{L}}{\partial{a}}=Sa-\lambda{a}=0$ ↔ $(S-\lambda{I})a=0$$
- $\lambda$ = eigenvalue = 각각의 principal component의 분산
- $\alpha$ = eigenvector
[Step 4]. Find the base set of bases
eigenvalues를 내림차순으로 정렬한다($\lambda_1 \geq \lambda_2 \geq ... \geq \lambda_d$). eigenvector $a_1$과 eigenvalue $\lambda_1$은 pairwise하게 존재한다(($\alpha_1, \lambda_1$)). $\alpha_1$에 사영되었을 때 보존되는 분산의 크기는 $\lambda_1$이다.
$$v = (a^T_1X)(a^T_1X)^T=a^T_1XX^Ta_1=a_1^TSa_1=a_1^T\lambda_1{a_1}=\lambda{a_1}^Ta_1=\lambda_1$$
혹은
$$Cov(X) = (e_1,e_2,..,e_p)\begin{pmatrix} \lambda_1 & 0 & .... & 0 \\ 0 & \lambda_2 & .... & 0 \\ ... \\ 0 & 0 & .... & \lambda_d \end{pmatrix}\begin{pmatrix} e_1 \\ e_2 \\ .... \\e_d \end{pmatrix} = \lambda_1e_1e_1^T + \lambda_2e_2e_2^T+...+\lambda_de_de_d^T$$
$$Var(a^Tx)=a^TSa=a^T(\lambda_1e_1e_1^T+...+\lambda_de_de_d^T)a \leq \lambda_1$$
결론적으로 first PC direction = $a_1 =e_1$ & first PC = $e_1^Tx=y_1$이다.
[Step 5].Extract the new features
$z = a_1^Tx$
[Step 6].Reconstruct the original data

1.4 Number of Principal Component
PCA에 사용할 PC의 개수를 명확하게 해결할 방법은 존재하지 않는다. 전문가의 사전 지식으로 결정하거나 보존되는 분산의 양으로부터 결정한다. 만약, 윌가 k번째 기저에 사영했을 때, 보존되는 분산의 양은 다음과 같다.
$\dfrac{\lambda_k}{\lambda_1+\lambda_2+\lambda_3+...+\lambda_k}$ ↔ 사전에 정한 비율을 통해 주성분 개수 정함.
또는, screen plot을 통해 PC의 수를 결정할 수 있다.

- x축: PC의 개수
- y축: 상응하는 eigenvalue 값(분산의 크기)
- Screen plot은 초기 단계에 급격하게 감소된다.
- Selection method 1: elbow point 선택
- Selection method 2: 사전에 결정된 분산 보존량을 만족하는 PC의 개수(cumulative variance w.r.t the number of PCs)
1.5 활용분야
PCA를 통해 이전에 발견하지 못한 관계성을 발견할 수도 있다. 즉, 새로운 해석이 가능하다. PCA는 변수끼리 높게 상관되어 있는 경우 매우 유용하며 PCA 결과는 multiple regression, classification 또는 cluserting의 input data로 활용 가능하다.
2. Multidimensional Scaling(MDS, 다차원 척도법)
2.1 Definition
다차원 척도법은 군집분석과 같이 객체들을 대상으로 변수들을 측정한 후에 객체들 사이의 유사성/비유사성을 측정하여 객체들을 2차원 공간상에 점으로 표현하는 분석기법이다. 즉, distance matrix(D)를 기반으로 저차원상의 각각의 객체가 갖는 좌표 시스템을 찾는 것이 목표이다. 다차원 척도법은 주로 거리를 바탕으로 이들 간의 관계 구조를 시각적으로 표현하는데 사용된다.
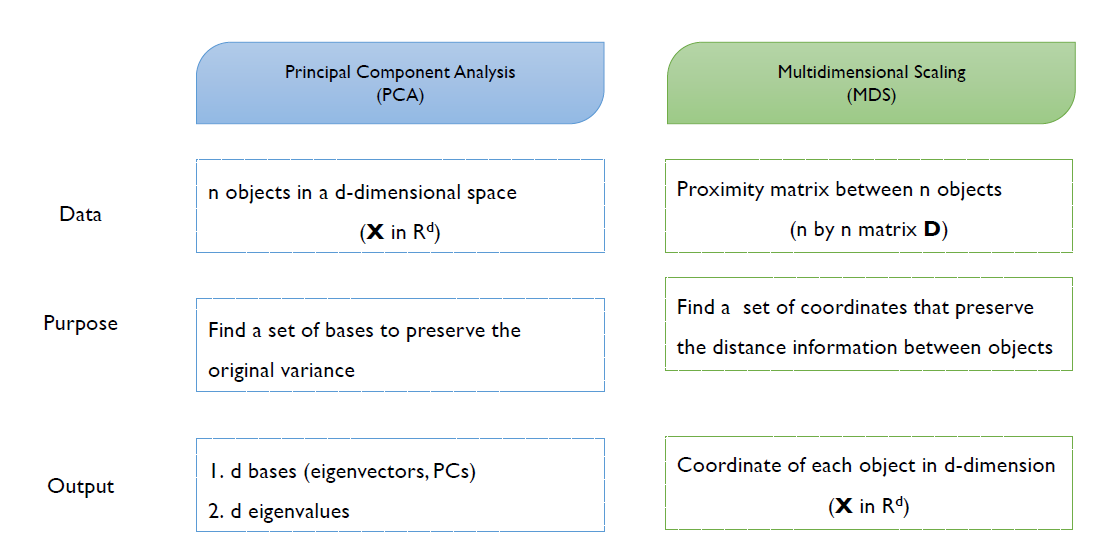
2.2 PCA vs. MDS
PCA는 데이터의 정보를 데이터가 가진 분산을 이용하지만 MDS는 데이터의 정보를 개별적인 객체들 사이의 거리(pairwise distance)를 이용한다는 점에서 큰 차이점이 존재한다.
2.3 Purpose
MDS를 통해 데이터 속에 잠재해 있는 패턴, 구조를 찾아낼 수 있으며 찾아낸 패턴과 구조를 소수 차원의 공간에 기하학적으로 표현 가능하다. 주로 데이터 축소를 목적으로 사용한다.
2.4 MDS Procedure
[Step 1]. Construct Proximity/Distance Matrix
객체들이 좌표계가 존재하는 경우, 그들 사이의 유사도/비유사도를 계산한다. distance(거리)는 다음 조건을 만족해야 한다.
- $d_{ij} \geq 0$
- $d_{ii}=0$
- $d_{ij} = d_{ji}$
- $d_{ij} \leq d_{ik}+d_{jk}$거
- 거리를 구하는 방법: Euclidean, Manhattan 등
- 유사도를 구하는 방법: Correlation, Jaccard 등
[Step 2]. Extract the coordinates that preserve the distance information
거리 정보를 보존하는 좌표시스템을 찾는 단계이다. 즉, 우리가 가진 정보인 distance matrix(D)를 통해 저차원 공간상에 존재하는 점을 찾는 단계이다.


참고자료
https://www.youtube.com/playlist?list=PLetSlH8YjIfWMdw9AuLR5ybkVvGcoG2EW
'Machine Learning > Dimensionality Reduction' 카테고리의 다른 글
| t-SNE (0) | 2023.01.02 |
|---|---|
| Local Linear Embedding(LLE) (0) | 2023.01.02 |
| ISOMAP (0) | 2023.01.01 |
| Supervised Selection - Forward/Backward/Stepwise (0) | 2022.12.21 |
| Dimensionaltiy Reduction의 필요성(차원축소 필요성) (0) | 2022.12.21 |



