LLE는 고차원 공간에서 인접해 있는 데이터들 사이의 선형적 구조를 보존하면서 저차원으로 임베딩하는 방법론이다. 즉, 좁은 범위에서 구축한 선형모델을 연결하면 다양체, 매니폴드를 잘 표현할 수 있는 알고리즘이다. ISOMAP과 LLE는 local한 정보를 이용해서 임베딩하는 점에서는 동일하지만, 어떻게 locality를 반영할지에 대해서는 다르다. LLE는 사용하기에 간단하며 최적화 시 local minimum으로 가지 않으며 비선형 임베딩 생성이 가능하다는 장점이 존재한다.
LLE 알고리즘
LLE의 전체적인 과정은 'Figure 1'과 같다. 먼저, 각 점으로부터 근접한 이웃을 선정한다. 근접한 이웃으로부터 선형적으로 가장 잘 재구성하는 가중치를 계산한 후, 가중치를 최대한 보존하는 embedding 공간 속에 있는 y 값을 찾는 것이다.
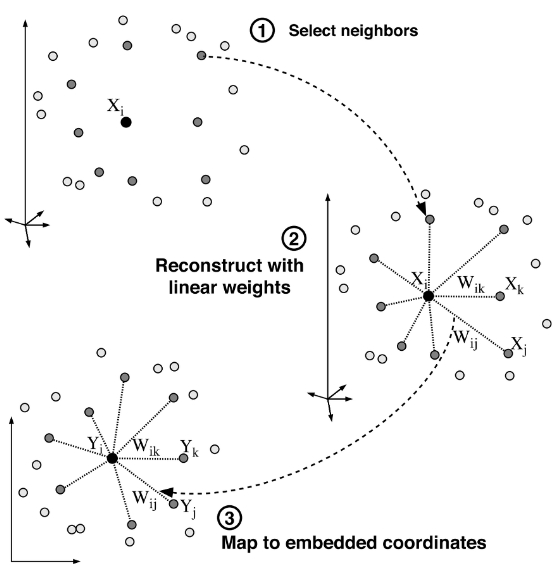
[Step 1] : Compute the neighbors of each data point
- i번째 객체($X_i$)로부터 근접한 이웃($X_j$)을 선정하는데 K-Nearest Neighbors 방법을 사용한다. ($i \in {1,2,...,n}$)
- KNN graph는 점들 간의 유클리디안 거리를 기반으로 형성된다.
- 그러므로, 모든 점은 k개의 이웃이 존재한다.
- $x_{ij} \in R^d$ : 객체 $x_i$의 j번째 이웃
- (1단계) 각 데이터 점의 이웃을 선택한다. 데이터 점들 간의 거리 계산 방법에는 대표적으로 K-Nearest Neighbor(KNN)이 존재한다.
- (2단계) 이웃으로부터 선형적으로 가장 잘 재구성하는 가중치를 계산한다.
- (3단계) 가중치를 사용해 저차원의 임베딩 좌표로 mapping한다. 앞서 구한 가중치를 최대한 보존하며 차원을 축소한다.
[Step 2]: Compute the weight $W_{ij}$ that best linear reconstruct each data point from its neighbors.
- 우리가 알고 있는 정보(특정 점의 k개의 이웃)로부터 선형적으로 특정 점을 가장 잘 복원(재구성)하는 가중치($W_{ij}$)를 계산하는 것이다.$$E(\hat{W}) = \sum^n_{i=1}||x_i-\sum^n_{j=1}x_j||^2_2, \, s.t. \, \sum^n_{j=1}\hat{w_{ij}}=1, \, i=\{1,..,n\}$$
- 위의 식을 최소화하는 $\hat{W}=[\hat{w_1},...,\hat{w_n}]$을 찾는 것이다.
[Step 3]: Compute the vectors best reconstructed by the weight $W_{ij}$, minimizing the quadratic from by its bottom nonzero eigenvectors.
- 가중치를 사용해 저차원의 임베딩 좌표로 mapping한다.
- 앞서 구한 가중치를 최대한 보존하며 차원을 축소한다.
- $X \in R^d$ → $Y \in R^P$ , $d>>p$
$$ min_{y}\Phi(W)=\sum^n_{i=1}||y_i-\sum^n_{j=1}w_{ij}y_j||^2_2, \, s.t. \, \dfrac{1}{n}\sum^n_{i=1}y_iy^t_i=I_p, \sum^n_{i=1}y_i= 0$$
- 위의 식을 변형하면 $min_{y}\Phi(W)=y^TMy, M=(I-W)^t(I-W)$과 같이 표현할 수 있으며 M의 eigenvector 및 eigenvalue를 사용해 차원 축소가 이루어진다.
LLE의 자세한 procedure 및 증명은 다음과 같다.


from scipy.sparse import linalg, eye
from pyamg import smoothed_aggregation_solver
from sklearn.neighbors import kneighbors_graph
import numpy as np
import pylab as pl
import matplotlib.pyplot as plt스위스 롤 Dataset 생성
n_samples, n_features = 2000, 3 ## 3차원 데이터
n_turns, radius = 1.2, 1.0
rng = np.random.RandomState(0)
t = rng.uniform(low=0, high=1, size=n_samples)
data = np.zeros((n_samples, n_features))
max_rot = n_turns * 2 * np.pi
data[:, 0] = radius = t * np.cos(t * max_rot)
data[:, 1] = radius = t * np.sin(t * max_rot)
data[:, 2] = rng.uniform(-1, 1.0, n_samples)
manifold = np.vstack((t * 2 - 1, data[:, 2])).T.copy()
colors = manifold[:, 0]
print(data.shape)
## (2000, 3)LLE Algorithm
[Step 1 & 2]
W = kneighbors_graph(data, n_neighbors=20, mode='distance') ## 거리 기반으로 n_neighbors만큼의 이웃 생성. ## 2000*2000 matrix 생성 ##symmetric matrix
print(W.shape)
#print(W)
print(W[0])
## 결과값에 나타나지 않는 값들은 모두 0
## 1번째 관측값(객체)을 복원하는데 사용된 관측값(객체)는 1797, 1337, 246, 1195,...,1344,327,1516번 객체
W = W.toarray()
print(W)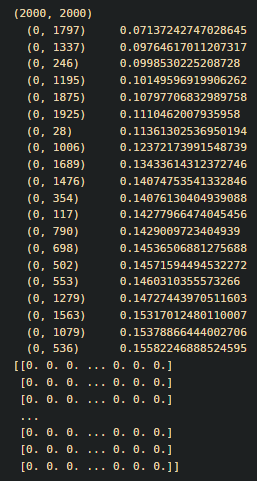
[Step 3]
A = eye(W.shape[0]) - W ## A = I-W
A = (A.T).dot(A) ## (I-W)^t(I-W)
print(A.shape)
print(A)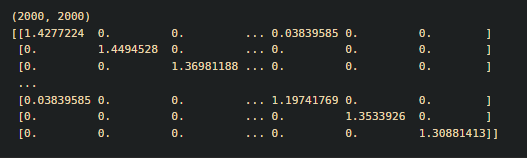
eigenvalue, eigenvector = np.linalg.eig(A)[0], np.linalg.eig(A)[1]
## eigenvalue 제일 작은 값 2개 찾기
index = np.argsort(eigenvalue)
#print(index)
X_r = eigenvector[:,index]plt.style.use('dark_background')
color='white'
plt.figure(figsize=(30,7))
plt.rcParams['text.color'] = color
plt.rcParams['axes.labelcolor'] = color
plt.rcParams['xtick.color'] = color
plt.rcParams['ytick.color'] = color
sp = pl.subplot(121)
U = np.dot(data, [[-.79, -.59, -.13],
[ .29, -.57, .75],
[-.53, .56, .63]])
sp.scatter(U[:, 1], U[:, 2], c=colors)
sp.set_title("Original data")
sp = pl.subplot(122)
sp.scatter(X_r[:,1].tolist(), X_r[:,2].tolist(), c=colors)
sp.set_title("LLE embedding")
pl.show()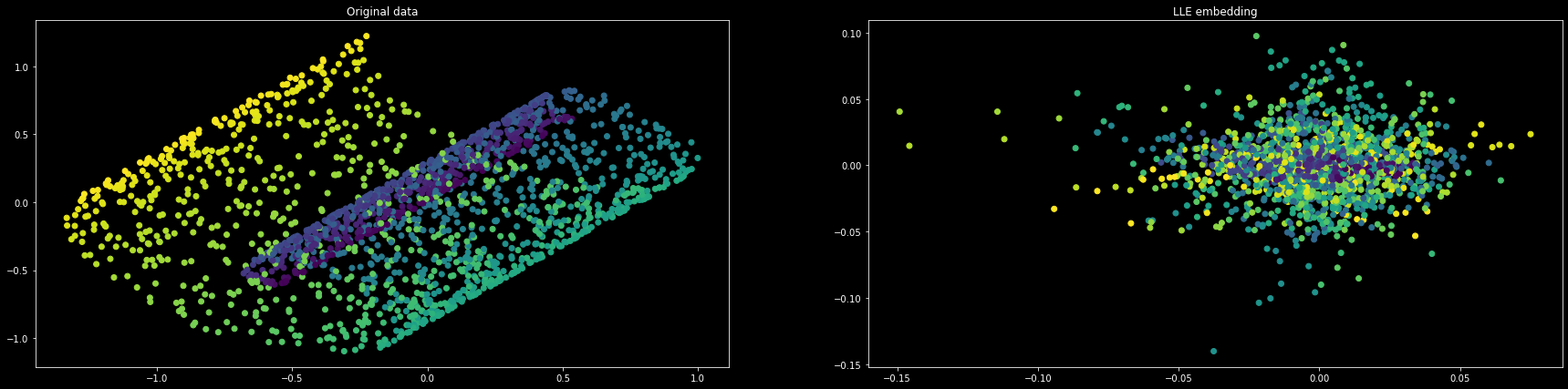
각 색깔은 각 class를 나타낸다. 이웃의 개수를 20개로 설정한 경우, 결과값은 오른쪽 그림과 같다.
3차원의 형태로 확인해보면 다음과 같다. 같은 분포에서 뽑아낸 값끼리 밀집해서 분포되어 있는 것을 확인할 수 있다.
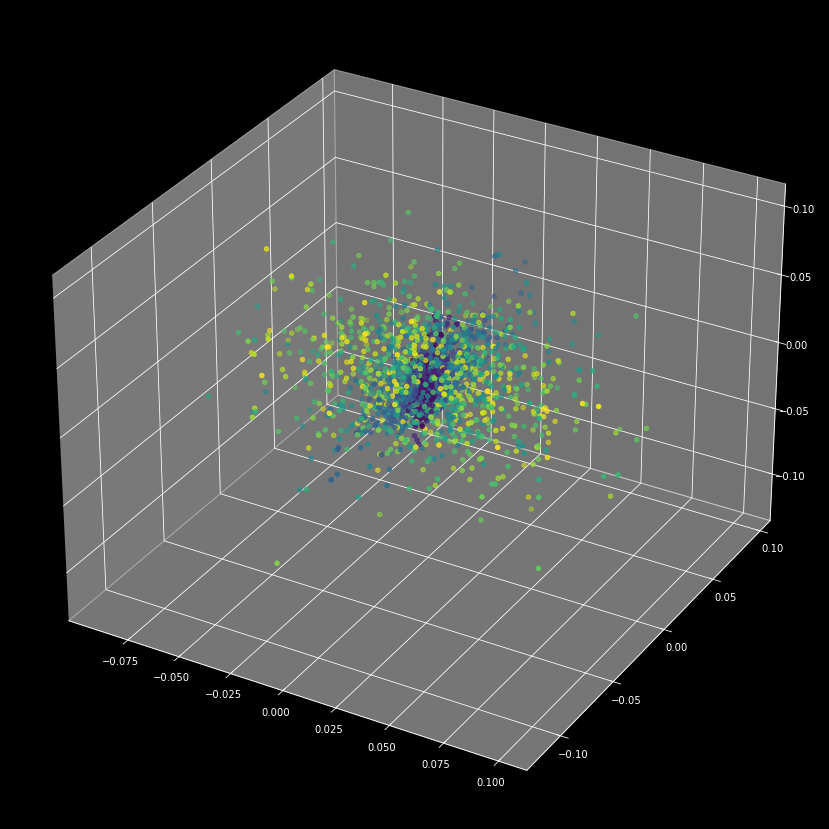
위의 과정을 하나의 함수로 표현하면 다음과 같다.
def locally_linear_embedding(X, n_neighbors):
W = kneighbors_graph(
X, n_neighbors=n_neighbors, mode='distance') ## 거리 기반으로 n_neighbors만큼의 이웃 생성.
W = W.toarray()
A = eye(W.shape[0]) - W
A = (A.T).dot(A)
eigenvalue, eigenvector = np.linalg.eig(A)[0], np.linalg.eig(A)[1]
index = np.argsort(eigenvalue)
return eigenvector[:, index], np.sum(eigenvalue)이웃의 개수(k 값)에 따른 다른 결과값을 확인해 볼 수 있다.
for i, n_neighbors in enumerate([2,5,10,12]):
X_r, cost = locally_linear_embedding(data, n_neighbors=n_neighbors)
plt.figure(figsize=(15,15))
ax = pl.subplot(2,2,i+1)
ax.scatter(X_r[:,1].tolist(),X_r[:,2].tolist(),c=colors)
ax.set_title('LLE with n_neighbors = {}'.format(n_neighbors))
이웃의 개수가 너무 적은 경우, 기존의 정보를 제대로 반영하지 않은 것을 알 수 있다. 즉, 객체 하나를 복원하는데 이웃하는 데이터의 정보를 적게 사용하면 차원 축소 결과 기존의 정보를 제대로 반영되지 않는다. k가 20, 30, 50, 70인 경우 결과값에 큰 차이가 없음을 알 수 있다. k가 20, 30, 50, 70인 경우에 대해서만 3d plot을 보면 다음과 같다.

3d plot을 확인해보면 이웃의 갯수에 따라 결과값이 다른 것을 알 수 있다. 기존의 정보를 최대한 잘 반영하기 위해서는 데이터마다의 특성에 따른 최적의 k 값을 찾는게 중요함을 알 수 있다.
'Machine Learning > Dimensionality Reduction' 카테고리의 다른 글
| t-SNE (0) | 2023.01.02 |
|---|---|
| ISOMAP (0) | 2023.01.01 |
| Principal Component(PCA) & Multidimensional Scaling(MDS,다차원 척도법) (0) | 2022.12.22 |
| Supervised Selection - Forward/Backward/Stepwise (0) | 2022.12.21 |
| Dimensionaltiy Reduction의 필요성(차원축소 필요성) (0) | 2022.12.21 |



