1. Definition
t-distributed stochastic neighbor embedding(t-SNE)는 높은 차원의 복잡한 데이터를 2차원에 축소하는 방법이다. t-SNE는 고차원의 벡터로 표현되는 데이터 간의 neighbor structure를 보존하는 2차원의 embedding vector를 학습함으로써 고차원의 데이터를 2차원의 지도로 표현한다. 낮은 차원 공간의 시각화에 주로 사용하며 차원 축소할 때는 비슷한 구조끼리 데이터를 정리한 상태이므로 데이터 구조를 이해하는데 도움이 된다. t-SNE는 데이터 간 거리를 stochastic probability로 변환하여 임베딩에 이용하기 때문에 다른 알고리즘보다 안정적인 임베딩 학습 결과를 가져온다. stochastic probability는 아래에서 설명할 perplexity에 의하혀 조절된다. t-SNE에 대해 설명하기 전에 SNE부터 설명해 보고자 한다.
2. Stochastic Neighbor Embedding(SNE)
SNE는 고차원 상에 있는 데이터 간의 관계를 반영하기 위해서 euclidean distance를 사용하여 확률을 정의한다.
- Stochastic = 각각의 데이터는 고정된 값이 아니라 확률을 가진다.
- Neighbor = 객체 j가 객체 i의 이웃이라면 객체 i의 정보를 복원할 때 이용되는 정보 양에 대한 높은 확률 값을 가진다.
- Embedding = 기존의 데이터 $x_i$를 $y_i$로 embedding 할 때 저차원 공간상에서의 확률분포 $Q_i$는 고차원 고간(기존의 공간) 상에서의 확률분포 $P_i$와 유사하도록 만들어줘야 한다.
2.1 SNE vs. LLE
<유사점>
- local한 distance를 보존하는 것이 local하지 않는 distance를 보존하는 것보다 훨씬 중요하다.
- LLE는 특정 데이터의 정보를 복원하는데 이웃의 정보를 이용한다. W(가중치) 값을 할당하여 원래 공간상에서의 재건축과 관련된 가중치를 계산한다. W를 그대로 보존하는 저차원의 좌표계를 찾는 방법이다.
- 기존 공간(고차원 공간)에서의 i와 j의 관계성이 저차원 공간에서의 i와 j의 관계성이 그대로 보존되어야 한다.
<차이점>
- LLE는 deterministic한 반면, SNE는 stochastic(확률적) 접근 방법론이 사용됨.
- 즉, SNE는 distance가 local인지 아닌지를 결정하는데 확률적으로 접근한다.
- 예를 들어, LLE의 경우, k=5인 경우 이웃의 변화가 없지만(복원하고자 하는 점으로부터 가장 가까운 점 5개만 이용), SNE의 경우 모든 점을 사용하며 대신 가까운 점에게 더 높은 확률값, 멀리 있는 점은 낮은 확률값을 가진다. 가까이 점은 특정 점을 복원하는데 기여도가 높지만 멀리 있는 점은 특정 점을 복원하는데 기여도가 낮기 떄문이다.
2.2 Non-Symmetric SNE
고차원 데이터의 유사성을 확률값(=한 객체가 다른 객체의 이웃으로 뽑힐 확률)으로 전환시킨다. 즉, 원 공간에서의 데이터 간 유사도 $p_{ij}$와 임베딩 공간에서의 유사도 $q_{ij}$를 정의해야 한다. $p_{ij}$를 정의하기 위해서 점 $x_i$에서 $x_j$로의 유사도인 $p_{j|i}$를 정의해야 한다.
$$ p_{j|i} = \dfrac{exp(-\dfrac{||x_i-x_j||^2}{2\sigma^2_i})}{\sum_{k\ne{i}}exp{-\dfrac{||x_i-x_k||^2}{2\sigma^2_i}}}, \, for \, all \, j \ne i, p_{i|i}=0$$
i는 고정된 값이며 j에 따라 변화는 확률값이다. 위의 식을 보면, 가우시안 확률밀도함수와 유사한 형태임을 알 수 있다.
$$ f(x) = \dfrac{1}{\sqrt{2\pi\sigma^2}}exp(-\dfrac{(x-\mu)^2}{2\sigma^2}) $$
위의 식을 해석해보면, 분자는 $x_i$는 고정된 값이므로 평균이 $x_i$이고, 표준편차가 $\sigma_j$인 가우시안 분포임을 알 수 있다( $\sigma_i$ : hyperparameter). $\sigma_i$는 객체마다 다른 값을 가지며 t-SNE가 안정적인 학습 결과를 가지게 하는데 결정적인 역할을 한다. 분모는 $\sum{p_{j|i}}=1$이 되도록 만들어주는 normalization term이다. $p_{j|i}$는 $x_i$가 $x_j$를 이웃으로 뽑을 확률이며 $x_j$가 $x_i$에 가까울수록 $p_{j|i}$의 값은 높아질 것이다.
임베딩 공간상에서의 유사도 $q_{j|i}$는 다음과 같이 정의된다.
$$q_{j|i} = \dfrac{exp(-||y_i-y_j||^2)}{\sum_{k\ne{i}}exp{-||x_i-x_k||^2}}$$
마찬가지로 평균은 $y_i$, 표준편차는 $\dfrac{1}{\sqrt{2}}$인 가우시안 분포의 형태를 띄는 것을 알 수 있다. SNE는 stochastic model으로 매 시점마다 확률분포를 따라 어떤 점이 다른 점으로 이동하는 모델이다. 즉, $y_j$는 $y_i$로부터 점점 가까워지거나 멀어지는 방향으로 이동하낟.
우리의 목표는 저차원에서 만든 $Q_i$들이 고차원에서 만든 $P_i$들과 최대한 비슷한 방향으로 $y_i$들을 업데이트 해나가는 것이다. 즉, SNE은 고차원상에서의 두 점들 간의 이웃 관계를 저차원상에서의 두 점들 간의 이웃 관계를 똑같이 확률적인 관계를 동일하게 만들고 싶은 것(즉, 분포를 똑같이 만들고 싶은 것)이다.
2.1 Kullback-Leibler Divergence
Kullback-Leibler Divergence는 두 분포간의 유사성을 판단하는데 사용된다.
- Cost Function: $\sum_iKL(P_i||Q_i)= \sum_i\sum_jp_{j|i}log{\dfrac{p_{j|i}}{q_{j|i}}}$
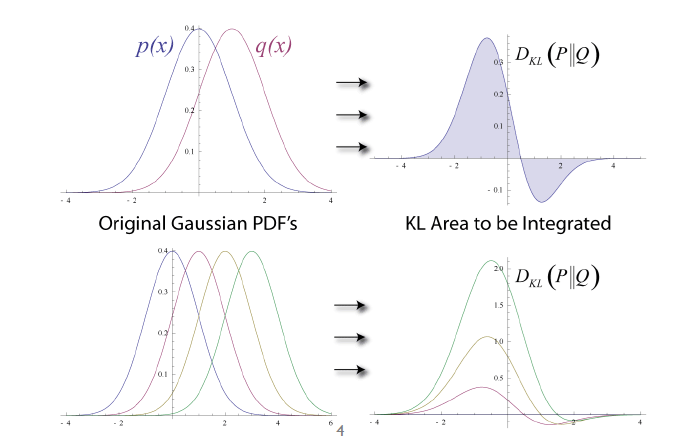
두 분포의 차이가 크면 클수록 cost 값은 증가한다. 결과적으로, Kullback-Leibler divergence는 고차원에서의 객체 i가 객체 j를 이웃으로 뽑을 확률분포와 저차원에서 객체 i가 객체 j를 이웃으로 뽑을 확률분포를 일치시킨다. Cost function을 C에 대하여 미분하면 다음과 같다.
- Minimizing C by using $\dfrac {\partial{C}}{\partial{y_i}} = 2\sum_j(p_{j|i}-q_{j|i}+p_{i|j}-q_{i|j})(y_{i}-y_{j})$
Cost Function이 낮아지는 방향으로 $y_j$들을 update 해 나아가면서 고차원의 확률분포화 점점 비슷해진다.
2.2 Cost Function의 역할
- $p_{j|i}$ 값에 따라 cost function에 반영되는 크기가 다름.
- 고차원에서 가깝게 있는 데이터를 저차원 에서 넓게 분포되어 있도록 embedding시킨 경우 큰 cost가 발생한다.
- 기존의 공간상에서 가까이 있는 경우, $p_{j|i}$ 값은 큰 반면, $q_{j|i}$는 작기 때문. → 큰 cost function 발생
- 고차원에서 멀리 있는 데이터를 저차원에서 가깝게 embedding 시킨 경우 작은 cost가 발생한다.
- 기존의 공간상에서 멀리 있는 경우, $p_{j|i}$ 값은 작은 반면, $q_{j|i}$는 작기 때문. → 작은 cost function 발생
- 고차원에서 가깝게 있는 데이터를 저차원 에서 넓게 분포되어 있도록 embedding시킨 경우 큰 cost가 발생한다.
- 즉, SNE은 고차원에서 가까이 있는 벡터들을 저차원에서도 가까이 있도록 만들어줌 ↔ 데이터의 local structure을 보존하는데 집중함.
- Gradient may be interpreted as the spring between the map point $y_i$ and $y_j$
- 만약, 고차원에서 멀리 떨어진 데이터가 저차원 상에서 가까이 mapping 되었다면 $p_{j|i}$의 값은 작지만 $q_{i|j}$의 값은 크게 됨.
-
- $\dfrac {\partial{C}}{\partial{y_i}} = 2\sum_j(p_{j|i}-q_{j|i}+p_{i|j}-q_{i|j})(y_{i}-y_{j})=0$
- $\dfrac {\partial{C}}{\partial{y_i}}=2\alpha(y_i-y_j)=0, \alpha<0$ ↔ 특정 객체 j에 대하여
- $(p_{j|i}-q_{j|i}+p_{i|j}-q_{}i|j)$의 값은 음수가 되어 $(y_i-y_j)$ 값의 반대 방향으로 업데이트. 즉, 서로 멀어지는 방향으로 업데이트가 될 것이다.
-
- 만약, 고차원에서 멀리 떨어진 데이터가 저차원 상에서 가까이 mapping 되었다면 $p_{j|i}$의 값은 작지만 $q_{i|j}$의 값은 크게 됨.
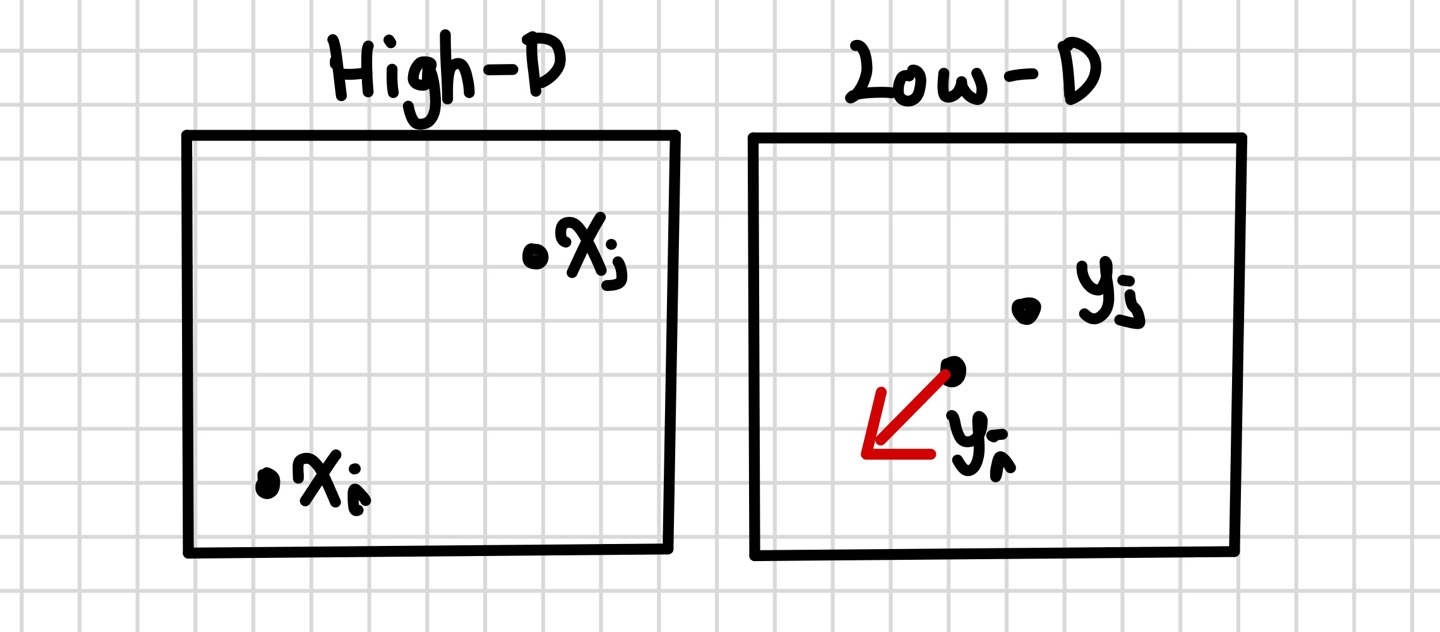
- 반대로, 고차원에서 가까이 있는 데이터가 저차원 상에서 멀리 mapping 되었다면 $p_{j|i}$의 값은 크지만 $q_{i|j}$의 값은 작게 된다.
- $(p_{j|i}-q_{j|i}+p_{i|j}-q_{}i|j)$의 값은 음수가 되어 $(y_i-y_j)$ 값의 방향으로 업데이트. 즉, 서로 가까워지는 방향으로 업데이트가 될 것이다.
- $\dfrac {\partial{C}}{\partial{y_i}} = 2\sum_j(p_{j|i}-q_{j|i}+p_{i|j}-q_{i|j})(y_{i}-y_{j})=0$
- $\dfrac {\partial{C}}{\partial{y_i}}=2\alpha(y_i-y_j)=0, \alpha>0$ ↔ 특정 객체 j에 대하여
- $(p_{j|i}-q_{j|i}+p_{i|j}-q_{}i|j)$의 값은 음수가 되어 $(y_i-y_j)$ 값의 방향으로 업데이트. 즉, 서로 가까워지는 방향으로 업데이트가 될 것이다.
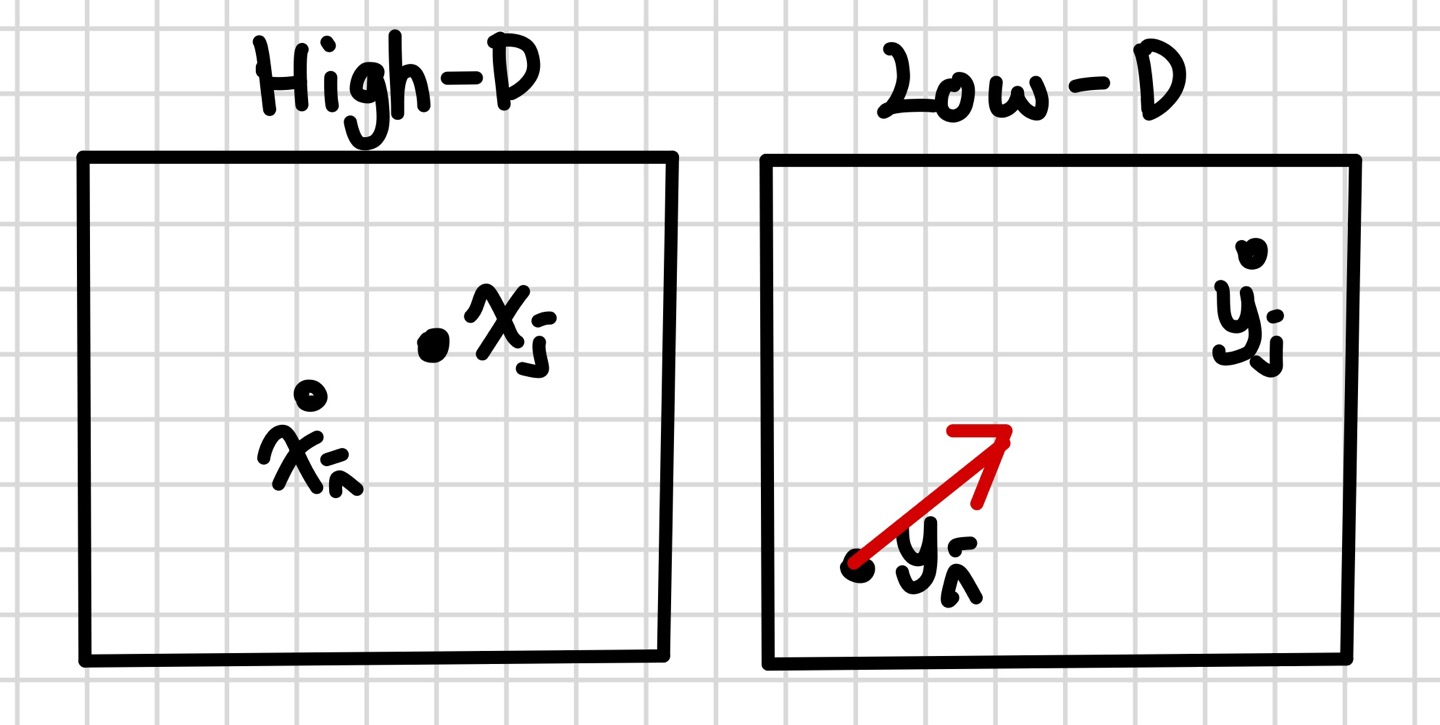
2.2 Symmetric SNE
$$p_{j|i} = \dfrac{exp(-\dfrac{||x_i-x_j||^2}{2\sigma^2_i})}{\sum_{k\ne{i}}exp{-\dfrac{||x_i-x_k||^2}{2\sigma^2_i}}} \ne p_{j|i} = \dfrac{exp(-\dfrac{||x_j-x_i||^2}{2\sigma^2_j})}{\sum_{k\ne{j}}exp{-\dfrac{||x_j-x_k||^2}{2\sigma^2_j}}}$$
위의 식을 대칭적으로(symmetric) 만들기 위한 2가지 방안이 존재한다.
- normalization term 변형하기
- 두 확률값의 평균 이용하기($\dfrac{p_{j|i}+p_{i|j}}{2}$)
첫번째 방법에 대해 먼저 설명해 보고자 한다.
Non-Symmetric SNE에서 사용한 $p_{j|i} = \dfrac{exp(-\dfrac{||x_i-x_j||^2}{2\sigma^2_i})}{\sum_{k\ne{i}}exp{-\dfrac{||x_i-x_k||^2}{2\sigma^2_i}}}$를 보면, 객체 마다 $\sigma_i$ 값이 다르며 특정 객체로부터의 다른 점들간의 거리를 계산하였다.
이를 다음과 같이 변형해준다.
$$ p_{ij}=\dfrac{exp(-\dfrac{||x_i-x_j||^2}{2\sigma^2})}{\sum_{k\ne{l}}exp(-\dfrac{||x_k-x_l||^2}{2\sigma^2})} $$
normalization term인 분모를 확인해 보면, 모든 객체에 동일한 $\sigma$ 값을 사용했으며 특정 객체로부터의 거리가 아닌 서로 다른 두 데이터간의 거리를 모두 더한 값이다.
임베딩 공간 상에서의 유사도 $q_ij$는 다음과 같이 정의된다.
$$q_{ij} = \dfrac{exp(-||y_i-y_j||^2)}{\sum_{k \ne l}exp(-||y_k-y_l||^2)}$$ $$q_{ij} = q_{ji}$$
하지만, 첫번째 방법의 경우 이상치에 민감하다는 단점이 존재한다.
두번째 방법은 두 확률값의 평균을 이용하는 것이다.
$$p_{j|i} = \dfrac{exp(-\dfrac{||x_i-x_j||^2}{2\sigma^2})}{\sum_{k\ne{i}}exp{-\dfrac{||x_i-x_k||^2}{2\sigma^2}}} \ne p_{j|i} = \dfrac{exp(-\dfrac{||x_j-x_i||^2}{2\sigma^2})}{\sum_{k\ne{j}}exp{-\dfrac{||x_j-x_k||^2}{2\sigma^2}}}$$
$$ p_{ij}=\dfrac{p_{j|i}+p_{i|j}}{2n} , \, \sum_j{p_{ij}} > \dfrac{1}{2n}$$
$$q_{ij} = \dfrac{exp(-||y_i-y_j||^2)}{\sum_{k \ne l}exp(-||y_k-y_l||^2)}$$
3. t-Stochastic Neighbor Embedding(t-SNE)
Symmetric SNE의 경우, 가우시안 분포의 형태가 중심으로부터 멀어질 때 일정 시점이 지난 경우 함숫값이 급격하게 감소하는 crowding 문제점이 존재한다. t-SNE는 crowding 문제점을 극복하기 위해 가우시안 분포보다 꼬리는 두껍고 중안은 덜 뾰족한 student t-분포를 사용한다.
$$p_{j|i} = \dfrac{exp(-\dfrac{||x_i-x_j||^2}{2\sigma^2})}{\sum_{k\ne{i}}exp{-\dfrac{||x_i-x_k||^2}{2\sigma^2}}} \ne p_{j|i} = \dfrac{exp(-\dfrac{||x_j-x_i||^2}{2\sigma^2})}{\sum_{k\ne{j}}exp{-\dfrac{||x_j-x_k||^2}{2\sigma^2}}}$$
$$ p_{ij}=\dfrac{p_{j|i}+p_{i|j}}{2n} , \, \sum_j{p_{ij}} > \dfrac{1}{2n}$$
$$q_{ij} = \dfrac{(1+||y_i-y_j||^2)^{-1}}{\sum_{k \ne l} (1+||y_k-y_l||^2)^{-1}}$$
$q_{ij}$는 자유도가 1인 t-분포이다.
- cost funciton: $C = KL(P||Q)=\sum_i\sum_jp_{ij}log\dfrac{p_{ij}}{q_{ij}}$
- Minimize by using $\dfrac {\partial{C}}{\partial{y_i}} = 4\sum_j(p_{ij}-q_{ij})(y_{i}-y_{j})(1+||y_i-y_j||^2)^{-1}$
- Gradient Descent with Momentum : $y^{(t+1)}=y^{(t)}+\eta\dfrac{\partial{C}}{\partial{y}}+\alpha{(t)}(y^{(t)}-y^{(t-1)})$
Gradient Descent with Momontum 식을 보면, 한 점 $y_i$에 대하여 자신이 이동해야 할 공간으로 이동하고 다음 점도 자신이 있어야 할 자리를 찾아 조금씩 이동한다.

모든 점들이 순차적으로 자신이 가야할 곳으로 이동하는 것을 반복하면 원 공간에서 가까운 점들이 임베딩 공간에서도 가까운 것을 알 수 있다.
'Machine Learning > Dimensionality Reduction' 카테고리의 다른 글
| Local Linear Embedding(LLE) (0) | 2023.01.02 |
|---|---|
| ISOMAP (0) | 2023.01.01 |
| Principal Component(PCA) & Multidimensional Scaling(MDS,다차원 척도법) (0) | 2022.12.22 |
| Supervised Selection - Forward/Backward/Stepwise (0) | 2022.12.21 |
| Dimensionaltiy Reduction의 필요성(차원축소 필요성) (0) | 2022.12.21 |



